TR NG THPT CHUYÊNƯỜ
HÀ TĨNH
Đ THI TH ĐI H C L N II NĂM 2013Ề Ử Ạ Ọ Ầ
Môn: TOÁN - Kh i: B, Dố
Th i gian làm bài: 180 phút, không k th i gian phát đờ ể ờ ề
PH N CHUNG CHO T T C THÍ SINH (7.0 Ầ Ấ Ả đi mể)
Câu I (2,0 đi m)ể Cho hàm s : ố
3
3 2y x x=−−
1) Kh o sát s bi n thiên và v đ th ả ự ế ẽ ồ ị
(C)
c a hàm s .ủ ố
2)Tìm t t c các giá tr ấ ả ị m đ đng th ng ∆ có h s góc m và đi qua đi m A(2; 0) c t đ th ể ườ ẳ ệ ố ể ắ ồ ị
(C)
t i ba đi m A, B, C phân bi t sao tam giác OBC có di n tích b ng ạ ể ệ ệ ằ
2 3
(O là g c t a đ)ố ọ ộ
Câu II. (2,0 đi m) ểGi i các ph ng trình sau:ả ươ
1) 1 + sinx – cosx = sin2x – cos2x
2)
x 4 x 4
x 1 3 x
−
+ =
− −
Câu III. (1,0 đi m)ểTính tích phân: I =
16
4 4
0
tan 4x dx
sin x cos x
π
+
Câu IV. ( 1,0 đi m)ể Cho hình chóp S.ABC có đáy ABC là tam giác đu c nh b ng a, m t bên (SAB)ề ạ ằ ặ
vuông góc v i đáy, hai m t bên (SAC) và (SBC) cùng t o v i đáy góc 45ớ ặ ạ ớ 0. M, N l n l t là trung đi mầ ượ ể
SB, SC.
Tính th tích kh i chóp A.BCMN theo a.ể ố
Câu V. ( 1.0 đi m)ể Cho các s th c d ng x,y,z th a mãn: x + y + z = 7.ố ự ươ ỏ
Tìm giá tr l n nh t c a bi u th c P = 15x + 8xy + 4xyz.ị ớ ấ ủ ể ứ
PH N RIÊNG (3,0 Ầđi mể): Thí sinh ch đc làm m t trong hai ph n (ph n A ho c B)ỉ ượ ộ ầ ầ ặ
A. Theo ch ng trình chu nươ ẩ :
Câu VIa ( 2,0 đi mể )
1. Trong m t ph ng t a đ Oxy, cho hình ch nh t ABCD có C(-2; 3); đng th ng ch a c nhặ ẳ ọ ộ ữ ậ ườ ẳ ứ ạ
CD đi qua đi m M(2; 1). Đng th ng ch a BD có ph ng trình: 2x + y – 11 = 0. Xác đnh t a đ cácể ườ ẳ ứ ươ ị ọ ộ
đnh còn l i c a hình ch nh t trên.ỉ ạ ủ ữ ậ
2. Trong không gian t a đ Oxyz, cho A(0; 1; 2 ), B(-1; 1; 0) và m t ph ng (P) có ph ng trình:ọ ộ ặ ẳ ươ
x + y + z + 1 = 0. Tìm t a đ đi m M ọ ộ ể
(P)
sao cho tam giác ABM vuông cân t i B.ạ
Câu VIIa ( 1,0 đi mể) Tìm t p h p các đi m trong m t ph ng ph c bi u di n các s ph c z th a mãn:ậ ợ ể ặ ẳ ứ ể ễ ố ứ ỏ
2 2
1 5 2013z z
− + − =
B. Theo ch ng trình nâng caoươ :
Câu VIb (2,0 đi mể)
1.Trong m t ph ng Oxy, cho hình bình hành ABCD có C( 3; -1), đng th ng ch a BD vàặ ẳ ườ ẳ ứ
đng th ng ch a đng phân giác c a góc ườ ẳ ứ ườ ủ
DAC
l n l t có ph ng trình là: x - 2y - 1 = 0 và x –ầ ượ ươ
1 = 0. Xác đnh t a đ các đnh còn l i c a hình bình hành trên.ị ọ ộ ỉ ạ ủ
2. Trong không gian t a đ Oxyz, cho đng th ng ọ ộ ườ ẳ
có ph ng trình: ươ
30
4
1975
x
y
z t
=
=
= +
Hai đi m A, B thay đi trên ể ổ
sao cho AB = 2 và hai đi m C, D thay đi trên tr c hoành sao cho CD =ể ổ ụ
3.
Tính th tích kh i t di n ABCD.ể ố ứ ệ
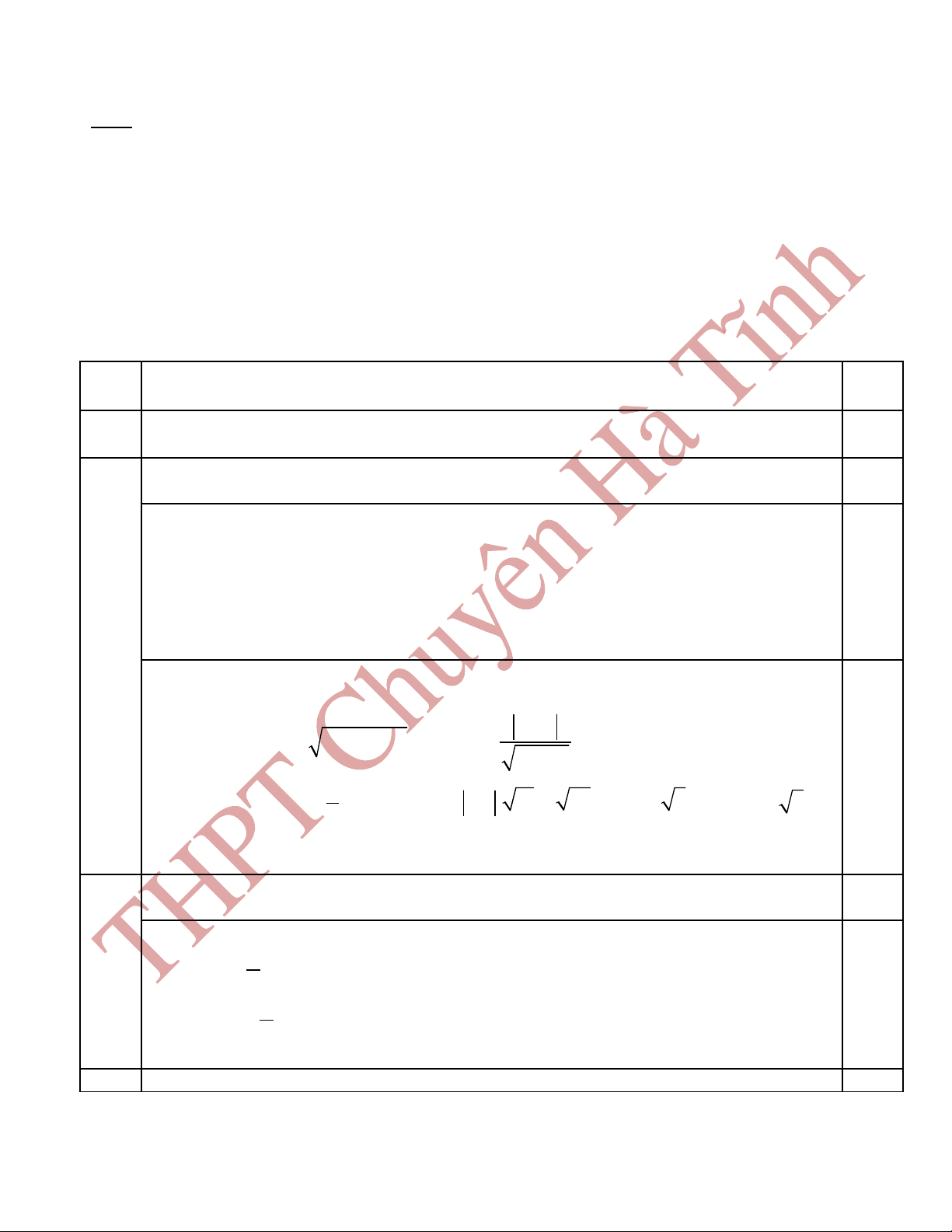
Câu VIIb ( 1,0 đi mể) Tìm t p h p các đi m trong m t ph ng ph c bi u di n các s ph c z th a mãnậ ợ ể ặ ẳ ứ ể ễ ố ứ ỏ
1
5
z
z i
−
−
là s th c.ố ự
................H t................ế
H tên thí sinh………….……………………….…..S báo danh………………..…… ọ ố
Thí sinh không s d ng tài li u - Th y, cô giáo xem thi không ph i gi i thích gì thêm.ử ụ ệ ầ ả ả
TR NG THPT CHUYÊNƯỜ
HÀ TĨNH
K THI TH ĐI H C L N II NĂM 2013Ỳ Ử Ạ Ọ Ầ
H NG D N CH MƯỚ Ẫ Ấ
Môn: TOÁN ; Kh i: B, Dố
Câu N i dungộĐiể
m
I.1 H c sinh t gi iọ ự ả 1,0
I.2
+ Ph ng trình đng th ng ∆: mx – y – 2m = 0.ươ ườ ẳ 0,25
+ Ph ng trình hoành đ giao đi m:ươ ộ ể
3 2
2
2 0
3 2 2 ( 2)( 2 1 ) 0 2 1 0(*)
x
x x mx m x x x m x x m
− =
− − = − − + + − =� � + + − =
+ ∆ c t (C) t i 3 đi m A, B, C phân bi t khi và ch khi pt(*) có 2 nghi m phân bi t ắ ạ ể ệ ỉ ệ ệ
khác 2
m > 0, m
9.
0,25
+ Khi đó A(2; 0). Đt ặ
( ;2 2 ), ( ;2 2 )B b b m C c c m− −
, v i b, c là hai nghi m phân bi t ớ ệ ệ
c a pt(*).ủ
Ta có: + BC =
2
2 (1 )m m
+
, d(O; ∆) =
2
2
1
m
m
−
+
Do đó:
3
1( ; ). 2 . 12 3
2
OBC
S d O BC m m m
∆
= ∆ = = =�
. V y ậ
3
3m
=
là
giá tr c n tìm.ị ầ
0,5
II.1
pt
(sinx-cosx)2+sinx-cosx – (sinx-cosx)(sinx+cosx)=0 0,5
(sinx-cosx)(1-2cosx)=0
4
2
3
x k
x k
ππ
ππ
= +
= +
0,5
Đi u ki n ề ệ
1 3.x
< <
0,25
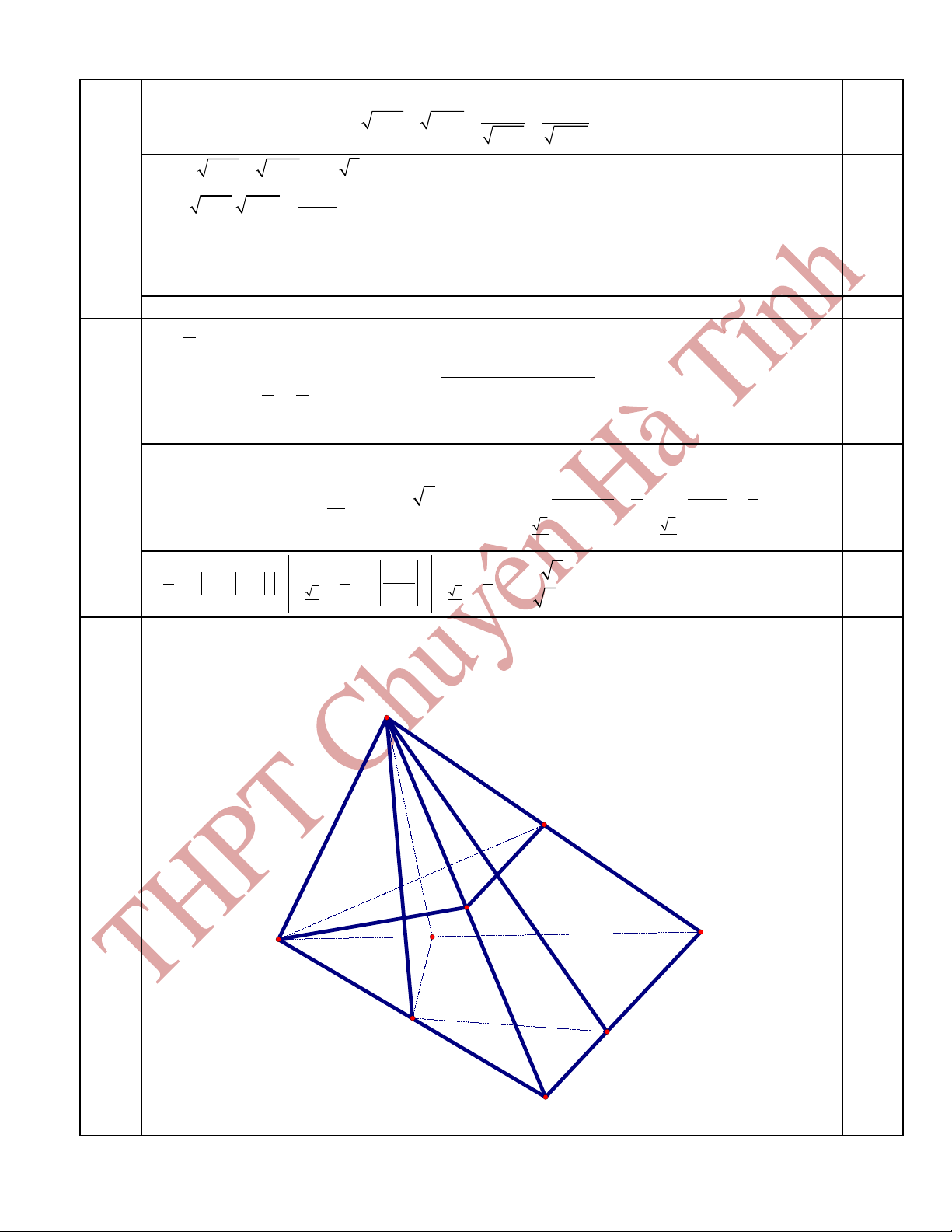
II.2
Ph ng trình đã cho t ng đng v i ptươ ươ ươ ớ :
1 1
1 3 4.
1 3
x x x x
− + − + + =
− −
0,25
Đt ặ
1 3x x t
− + − =
( 2 2)t
<
(*)
ta có
2
2
1. 3 .
2
t
x x −
− − =
Khi đó ph ng trình tr thànhươ ở
3 2
2
24 4 8 0
2
t
t t t
t
+ = − + =�
−
2
( 2)( 2 4) 0t t t
− − − =
t = 2 ( do đ/k (*))
0,25
V i t = 2 gi i ra x = 2 . Đáp s x = 2ớ ả ố 0,25
III
I =
16
0
sin 4x dx
3 1
cos4x( cos4x)
4 4
π
+
= 4
16
0
sin 4x dx
cos4x(3 cos4x)
π
+
0,25
Đt t = 3+cos4x ặ
dt= - 4sin4xdx
Khi x=0 thì t=4; khi x=
16
π
thì t=3+
2
2
V y I = ậ
4
2
32
dt
(t 3)t
+
−
=
4
2
32
1 1 1
( )dt
3 t 3 t
+
−
−
0,5
=
(ln
3t
−
-ln
)
4
2
32
+
=
(
3
ln t
t
−
)
4
2
32
+
=
ln
6 2
4 2
+
0,25
IV
N
M
H
A
B
C
S
E
F
0,25
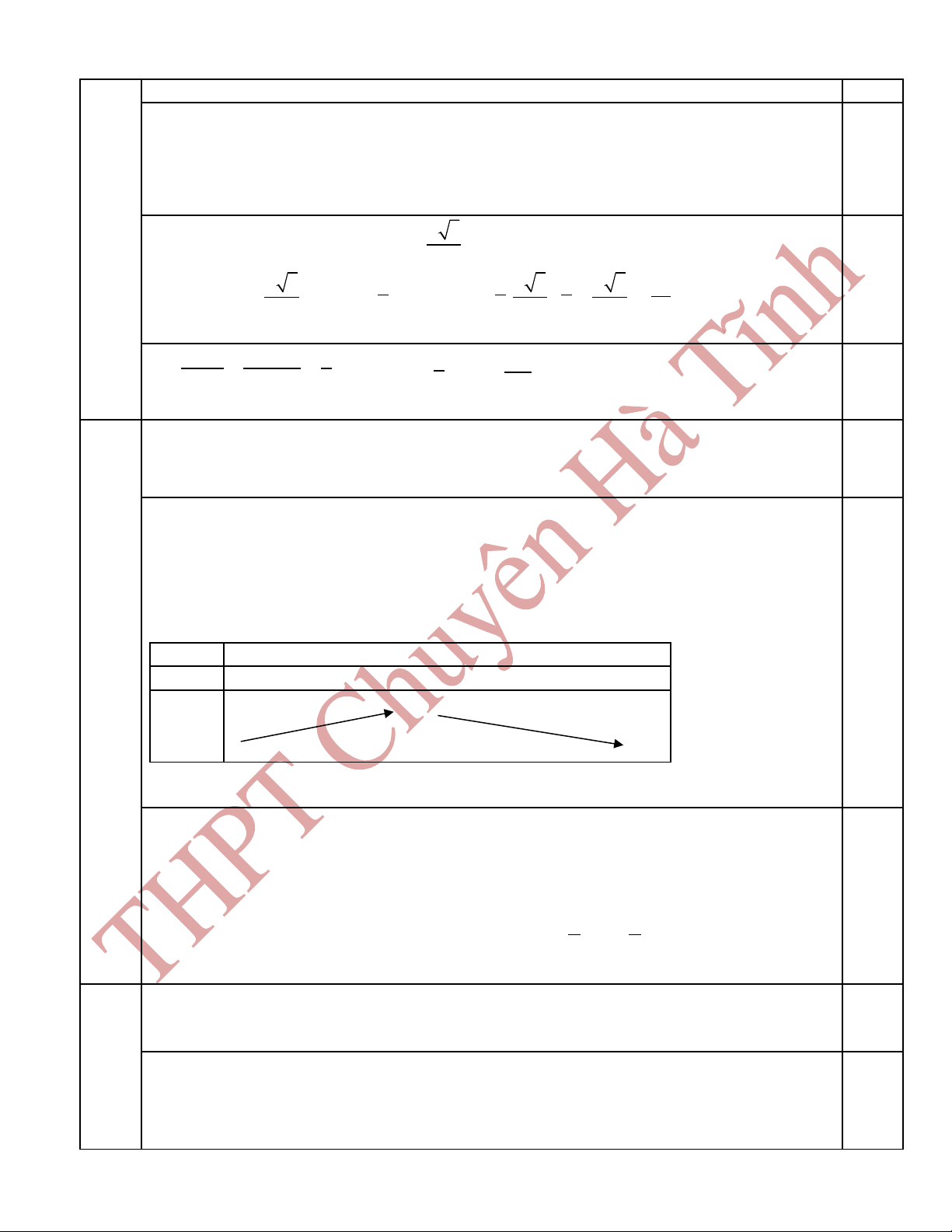
K SH ẻ
⊥
AB
SH
⊥
(ABC). K HEẻ
⊥
BC
BC
⊥
(SHE )
BC
⊥
SE
SEH=45o
T ng t ươ ự
SFH=45o
Hai tam giác vuông SHE và SHF b ng nhau suy ra HE=HF ằ
H n m trên đng ằ ườ
phân giác góc C c a tam giác đu ABC ủ ề
H là trung đi m ABể0,25
Ta có: HE.BC=CH.HB
HE =
3
4
a
SH= HE =
3
4
a
; VSABC=
SH.S
ABC =
3
4
a
(
1
2
a.
3
2
a
)=
3
16
a
0,25
. 1
. 4
SAMN
SABC
VSM SN
V SB SC
= =
VABCMN =
3
4
SABC
V
=
3
3
64
a
0,25
V
Ta có: P = 15x + 4x[ y(2 + z ) ]
2
15x x[y (2 z)] + + +
0,25
=
2 3 2
15x x(9 x) x 18x 96x f (x)+ − = − + =
Khi đó:
' 2
f (x) 3x 36x 96 0= − + =
x 4
x 8
=
=
Ta xét b ng bi n thiên: ả ế
X 0 4 7
F'(x) + 0 -
F(x) 160
0,5
V y P đt giá tr l n nh t b ng 160 khi:ậ ạ ị ớ ấ ằ
x y z 7
y 2 z
x 4
+ + =
= +
=
t c là khi: x = 4, y = ứ
5
2
,
1
z2
=
.
0,25
Via.1 -Ph ng trình CD: x + 2y – 4 = 0ươ
-T a đ D(6;-1)ọ ộ 0,25
-Ph ng trình đng th ng CB: 2x – y + 7 = 0ươ ườ ẳ
-B=CB
BD=(1;9)
0,25
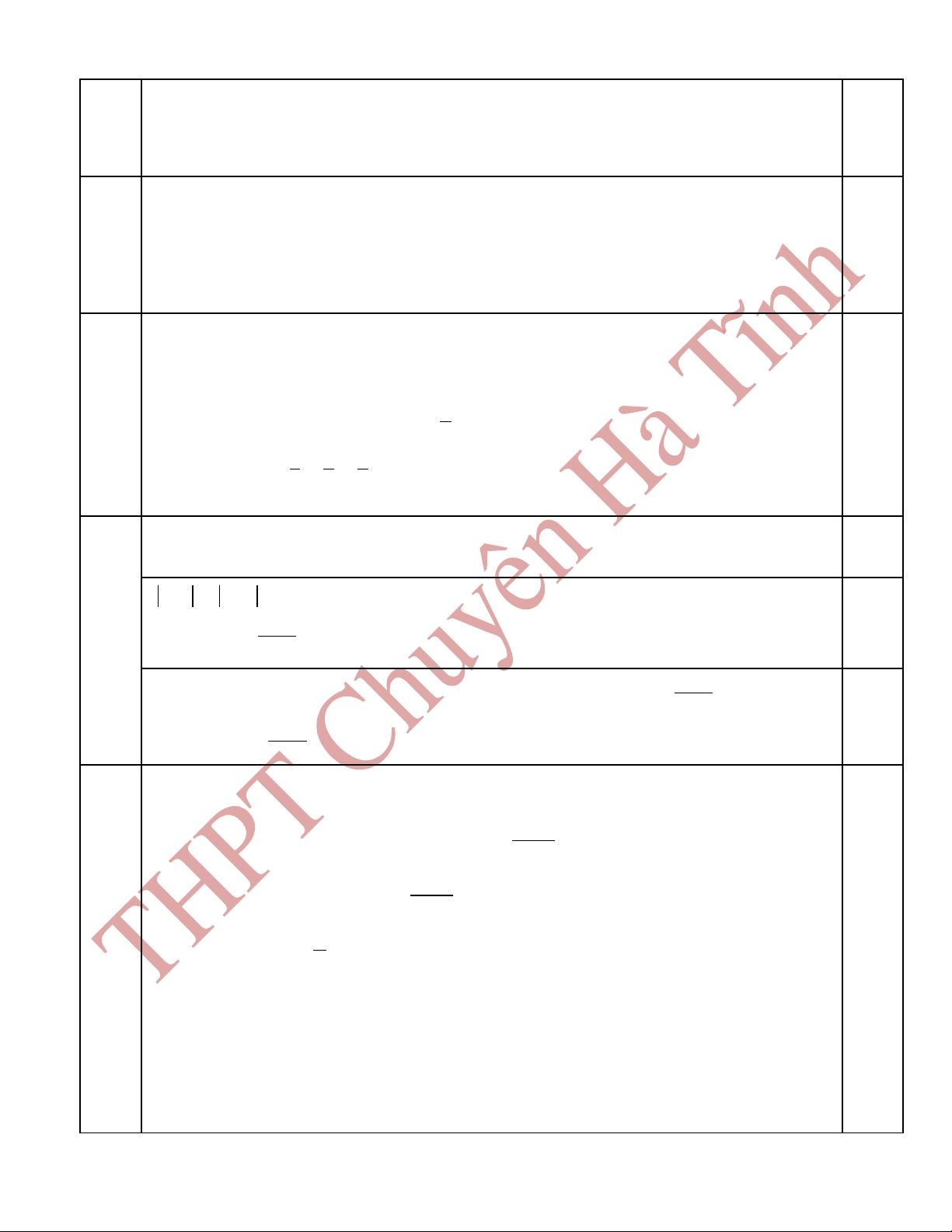
-I là trung đi m BD => I(7/2;4)=> A(9;5)ể
K t lu n: A(9;5); B(1;9);C(-2;3);D(6;-1)ế ậ 0,5
Via.2 G i t a đ M(xọ ọ ộ 0; y0; z0) suy ra
0 0 0
( 1; 1; ), ( 1;0; 2)BM x y z AB= + − = − −
uuuur uuur
Đ tam giác ABM vuông cân t i M và M ể ạ
( )P
, ta c n cóầ :
( )
. 0
M P
AB BM
BM AB
=
=
uuur uuuur
0,5
0 0 0
0 0
2 2 2
0 0 0
1 0
1( 1) 2 0
( 1) ( 1) 5
x y z
x z
x y z
+ + + =
− + − =�+ + − + =
Gi i theo zả0 ta có : z0 = 1 ho c zặ0 =
2
3
−
suy ra có 2 đi m M c n tìm là:ể ầ
M (-3; 1; 1) và M(
1 2 2
; ; )
3 3 3
− −
0,5
VII.a G i z = a + bi và M(aọ ;b) là đi m bi u di n z trên m t ph ng ph c.ể ể ễ ặ ẳ ứ
z – 1 = a – 1 + bi ; z – 5 = a – 5 + bi 0,25
2 2
1 5 2013z z
− + − =
(a-1)2+b2+(a-5)2+b2=2013
a2+b2-6a -
1987
2
= 0 0,5
V y t p h p các đi m M là đng tròn có ph ng trình: xậ ậ ọ ể ườ ươ 2+y2-6x -
1987
2
= 0
hay: (x-3)2+y2=
2005
2
0,25
Vib.1 + G i C’ là đi m đi x ng c a C qua đng phân giác góc ọ ể ố ứ ủ ườ DAC.
Khi đó C’(-1 ; -1).
+ Đt A( 1ặ ; a), khi đó tâm hình bình hành
1
(2; )
2
-a
I
là trung đi m AC và thu c đngể ộ ườ
th ng ch a c nh BD nênẳ ứ ạ :
1
2 2. 1 0 2
2
-
- - = =�
aa
Do đó A( 1 ; 2),
1
(2; )
2
I
.
+ Ta suy ra ph ng trình đng th ng AC’ làươ ườ ẳ :3x – 2y +1 =0.
Khi đó t a đ D là nghi m c a h ph ng trìnhọ ộ ệ ủ ệ ươ :
2 1 0
3 2 1 0
￬- - =
￬
￬
￬
￬- + =
￬
￬
x y
x y
Ta đc D( -1ượ ; -1), t đó suy ra B( 5ừ ; 3).
+ V y t a đ các đnh còn l i c a hình bình hành ABCD làậ ọ ộ ỉ ạ ủ : A( 1 ; 2), B( 5 ; 3), D( -1 ;
-1).
0,25
0,25
0,25
0,25