zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Tài Liệu Phổ Thông

» Ôn thi ĐH-CĐ

Đề thi thử ĐH lần 1 Toán khối A, A1, B, D (2013-2014) – THPT Lục Ngạn số 1

Chia sẻ: Nguyen Phuoc Vinh | Ngày: | Loại File: PDF | Số trang:7

Báo xấu

67
lượt xem 3
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Với nội dung: Khảo sát sự biến thiên và vẽ đồ thị hàm số, tìm giá trị lớn nhất và nhỏ nhất, trọng tâm của tam giác...đề thi thử Đại học lần 1 môn Toán khối A, A1, B, D năm 2013-2014 của trường THPT Lục Ngạn số 1 sẽ giúp các bạn học sinh có cơ hội thử sức của mình với các đề thi trước khi vào đề thi chính thức. Mời các bạn tham khảo.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi thử ĐH lần 1 Toán khối A, A1, B, D (2013-2014) – THPT Lục Ngạn số 1

www.VNMATH.com S GD& T B c Giang THI TH IH CL N1 Tr ng THPT L c Ng n s 1 N M H C 2013 - 2014 Môn: Toán - kh i A, A1, B, D. chính th c Th i gian làm bài 180 phút, không k th i gian phát I. PH N CHUNG CHO T T C THÍ SINH ( 7 i m) Câu 1 (2 i m). Cho hàm s y = 2 x3 − 3(2m + 1) x2 + 6m(m + 1) x + 1 có th (1). a) Kh o sát s bi n thiên và v th c a hàm s (1) khi m = 0. b) Tìm m hàm s (1) ng bi n trên kho ng (2;+∞ ) cos 2 x + cos3 x − 1 Câu 2 (1 i m). Gi i ph ng trình sau: cos 2 x − tan 2 x = cos 2 x Câu 3 (1 i m). Gi i ph ng trình sau: 7 - x 2 + x x + 5 = 3 - 2x - x 2 (x ∈ R) Câu 4 (1 i m). Tìm m h ph ng trình sau có 3 c p nghi m th c phân bi t: 3( x + 1)2 + y = m xy = 1 − x Câu 5 (1 i m). Cho hình chóp t giác S.ABCD có áy là hình ch nh t, SA vuông góc v i áy, G là tr ng tâm tam giác SAC, m t ph ng (ABG) c t SC t i M, c t SD t i N. Tính th tích c a kh i a di n MNABCD bi t SA=AB=a và góc h p b i ng th ng AN và mp(ABCD) b ng 300 . Câu 6 (1 i m) Cho x,y,z tho mãn là các s th c: x 2 - xy + y 2 = 1 .Tìm giá tr l n nh t và giá tr nh nh t c a bi u th c: x 4 + y4 + 1 P= x 2 + y2 + 1 II. PH N RIÊNG (3 i m): Thí sinh ch c làm m t trong hai ph n ( Ph n A ho c ph n B). A. Theo ch ng trình chu n Câu 7a (1 i m). Trong m t ph ng Oxy, cho tam giác ABC v i AB = 5 , C(-1;-1), ng th ng AB có ph ng trình: x + 2y – 3 = 0 và tr ng tâm tam giác ABC thu c ng th ng d: x + y – 2 = 0 . Tìm to !nh A và B. Câu 8a (1 i m). Trong m t ph ng v i h to Oxy, cho ng tròn (C): x 2 + y 2 - 4x - 4y + 4=0 và ng th ng d có ph ng trình: x + y - 2=0 . Ch ng minh r ng d luôn c t (C) tai hai i m phân bi t A và B. Tìm to i m M trên ng tròn (C) sao cho di n tích tam giác MAB l n nh t. Câu 9a (1 i m). Cho khai tri n: (1 + x + x 2 ) = a 0 + a1x + a 2 x 2 +...+a 24 x 24 . Tính a 4 . 12 B. Theo ch ng nâng cao Câu 7b (1 i m). Trong m t ph ng Oxy, cho tam giác ABC bi t B(2;-1), ng cao và phân giác trong qua !nh A và C l"n l t có ph ng trình: 3x – 4y + 27 = 0 và x + 2y – 5 = 0. Vi t ph ng trình các c nh c a tam giác ABC. Câu 8b (1 i m). Trong m t ph ng Oxy, vi t ph ng trình chính t c c a Elíp (E), bi t r ng tâm sai 5 c a (E) b ng và hình ch nh t c s có di n tích b ng 24. 3 Câu 9b (1 i m). M t h p ng 15 viên bi, trong ó có 7 viên bi xanh và 8 viên bi . L y ng#u nhiên 3 viên bi (không k th t ra kh i h p). Tính xác xu t trong 3 viên bi l y ra có ít nh t 1 viên bi . ............H t........... Chú ý: Giáo viên coi thi không gi i thích gì thêm. H và tên thí sinh:.......................................................S bao danh:........................
www.VNMATH.com H NG D N CH M VÀ CHO I M Môn: Toán (Thi Th H l n 1 - N m h c 2013 - 2014) Câu N i dung c b n i m Câu 1 Cho hàm s y = 2 x3 − 3(2m + 1) x2 + 6m(m + 1) x + 1 có th (Cm). 2 a) Kh o sát s bi n thiên và v th c a hàm s khi m = 0. b) Tìm m hàm s ng bi n trên kho ng (2;+∞ ) a V i m = 0 ta có: y = 2x – 3x2 + 1 3 (1 ) *TX : R * Gi i h n: lim y = +∞; lim y = −∞ x →+∞ x →−∞ *S bi n thiên: Ta có y’ = 6x2 – 6x =6x(x-1) = 0 x = 0; x= 1 0.5 x -∞ 0 1 +∞ y’ + 0 - 0 + 1 +∞ y -∞ 0 * k t lu n ng bi n, ngh ch bi n và c c tr . 0.25 * Ch! ra to i m u n U(1/2;1/2), Hs có th b qua b c này *V th : 0,25 1 1 O b y = 2 x3 − 3(2m + 1) x2 + 6m(m + 1) x + 1 y ' 6 x 2 − 6(2m + 1) x + 6m(m + 1) = (1 ) 0.5 y’ có ∆ = (2m + 1) 2 − 4(m 2 + m) = 1 > 0 x=m y' 0 ⇔ = x = m +1 0.25
www.VNMATH.com Hàm s ng bi n trên (2;+∞ ) ⇔ y ' 0 ∀x > 2 ⇔ m + 1 ≤ 2 ⇔ m ≤ 1 > m ≤1 0.25 Câu 2 cos 2 x + cos3 x − 1 1 Gi i ph ng trình sau: cos 2 x − tan 2 x = cos 2 x K cosx $ 0, pt c av cos 2 x − tan x = 1 + cos x − (1 + tan 2 x) ⇔ 2cos 2 x − cos x -1 = 0 2 0.5 Gi i ti p c cosx = 1 và cosx = 0,5 r i i chi u k a ra S: 2π 2π 0.5 x = k 2π , x = ± + k 2π ; hay x = k . 3 3 Câu 3 Gi i ph ng trình sau: 7 - x 2 + x x + 5 = 3 - 2x - x 2 (x ∈ R) 1 3 − 2 x − x2 ≥ 0 0.25 PT ⇔ 7 − x2 + x x + 5 = 3 − 2 x − x2 3 − 2 x − x2 ≥ 0 0.25 ⇔ x x + 5 = −2( x + 2) 0.25 −3 ≤ x ≤ 1 −2 ≤ x < 0 ⇔ x≠0 ⇔ ( x + 1) ( x 2 − 16 ) = 0 x+2 x + 5 = −2. x ⇔ x = −1 0.25 V y ph ng trình ã cho có m t nghi m x = - 1. Câu 4 Tìm m h ph ng trình sau có 3 c p nghi m th c phân bi t: 1 3( x + 1) 2 + y = m, (1) xy = 1 − x, (2) x ≤1 1− x ≥ 0 (2) 1 ( do x = 0 không là nghi m) 0,25 xy = (1 − x)2 y= −2+ x x 1 Th vào (1) ta có: 3( x + 1)2 + − 2 + x = m , (3) x 1 0,5 Xét hàm s f(x) = 3( x + 1) 2 + − 2 + x trên ( −∞;1] , l p b ng bi n thiên. x L p lu n c m%i giá tr x trên ( −∞;1] thì có duy nh t 1 giá tr y, nên (3) có 3 nghi m phân bi t 20 0,25 < m ≤ 12 KL: 3 −15 < m < −4 4
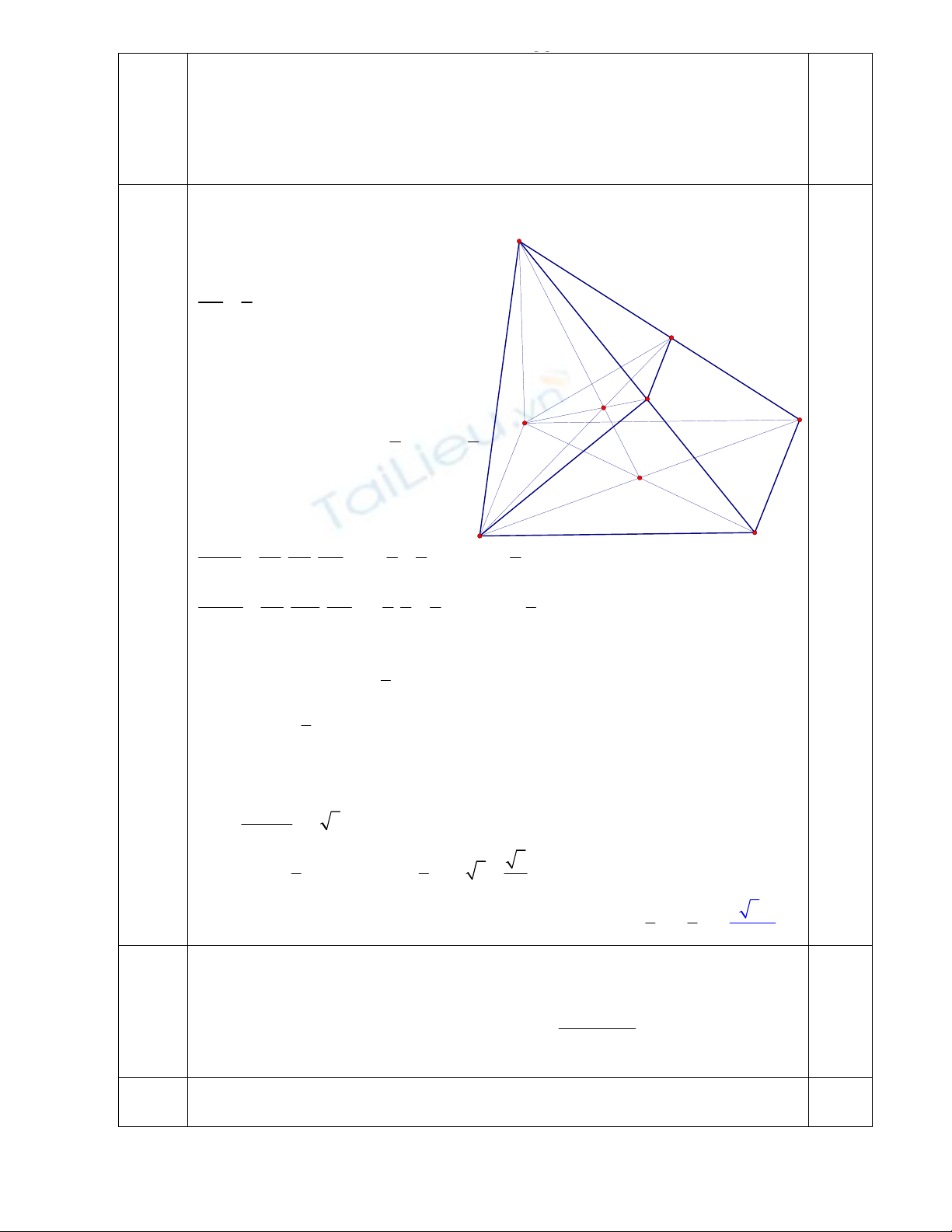
www.VNMATH.com Câu 5 Cho hình chóp S.ABCD có áy là hình vuông c nh b ng a. m t bên SAB là 1 tam giác vuông cân nh S và n m trong m t ph ng vuông góc v i m t ph ng áy. Tính theo a th tích kh i chóp S.ABCD và tính kho ng cách gi a hai ng th ng AB và SD. + Trong mp(SAC) k& AG c t SC t i M, trong mp(SBD) k& BG c t SD t i N. S + Vì G là tr ng tâm tam giác ABC nên d' có SG 2 = suy ra G c(ng là tr ng SO 3 N tâm tam giác SBD. T) ó suy ra M, N l"n l t là trung i m c a M G SC, SD. A D 1 1 + D' có: VS . ABD = VS .BCD = VS . ABCD = V . 2 2 O Theo công th c t* s th tích ta có: B C VS . ABN SA SB SN 1 1 1 = . . = 1.1. = VS . ABN = V VS . ABD SA SB SD 2 2 4 0,5 VS .BMN SB SM SN 1 1 1 1 = . . = 1. . = VS . BMN = V VS .BCD SB SC SD 2 2 4 8 T) ó suy ra: 3 VS . ABMN = VS . ABN + VS . BMN = V . 8 1 + Ta có: V = SA.dt ( ABCD ) ; mà theo gi thi t SA ⊥ ( ABCD) nên góc h p 3 b i AN v i mp(ABCD) chính là góc NAD , l i có N là trung i m c a SC nên tam giác NAD cân t i N, suy ra NAD = NDA = 300. Suy ra: SA AD = =a 3. tan 300 1 1 3 Suy ra: V = SA.dt ( ABCD) = a.a.a 3 = a3 . 3 3 3 3 5 5 3a 3 Suy ra: th tích c"n tìm là: VMNABCD = VS . ABCD − VS . ABMN = V − V = V = . 0,5 8 8 24 Câu 6 Cho x,y,z tho mãn là các s th c: x 2 - xy + y 2 = 1 .Tìm giá tr l n nh t và giá 1 tr nh nh t c a bi u th c: x 4 + y4 + 1 P= x 2 + y2 + 1 0,25
www.VNMATH.com 1 = x 2 − xy + y 2 ≥ 2 xy − xy = xy 1 = ( x + y ) 2 − 3 xy ≥ −3 xy 1 − ≤ xy ≤ 1 3 x 2 − xy + y 2 = 1 ⇔ x 2 + y 2 = 1 + xy x 4 + y 4 = − x 2 y 2 + 2 xy + 1 ! # " $%# $$ & 0,25 − t 2 + 2t + 2 1 P = f (t ) = ;− ≤ t ≤ 1 t+2 3 6 t = 6 −2 ' f 't ) = 0 ⇔ −1 + ( =0⇔ 0,25 (t + 2) 2 t = − 6 − 2(l ) 1 ( " )* + [ − ;1] ,& 3 −1 f( ) % f ( 6 − 2) % f (1) - 3 0,25 1 11 MaxP = f ( 6 − 2) = 6 − 2 6 % min P = f (− ) = 3 15 Câu Trong m t ph ng Oxy, cho tam giác ABC v i AB = 5 , C(-1;-1), ng 7a th ng AB có ph ng trình: x + 2y – 3 = 0 và tr ng tâm tam giác ABC thu c (1 ) ng th ng d: x + y – 2 = 0 . Tìm to nh A và B. * Gi s+ A(3-2a ; a); B(3 - 2b; b) 0,25 * Tính tr ng tâm tam giác G. Vì G thu c d nên ta có: 0,25 * M t khác AB = 5 . 3 1 3 1 0,5 * T) ó gi i h ta c: A 6; − ; B 4; − ho c B 6; − ; A 4; − 2 2 2 2 Câu Trong m t ph ng v i h to Oxy, cho ng tròn (C): 8a x + y - 4x - 4y + 4=0 và 2 2 ng th ng d có ph ng trình: x + y - 2=0 . Ch ng (1 ) minh r ng d luôn c t (C) tai hai i m phân bi t A và B. Tìm to i mM trên ng tròn (C) sao cho di n tích tam giác MAB l n nh t. 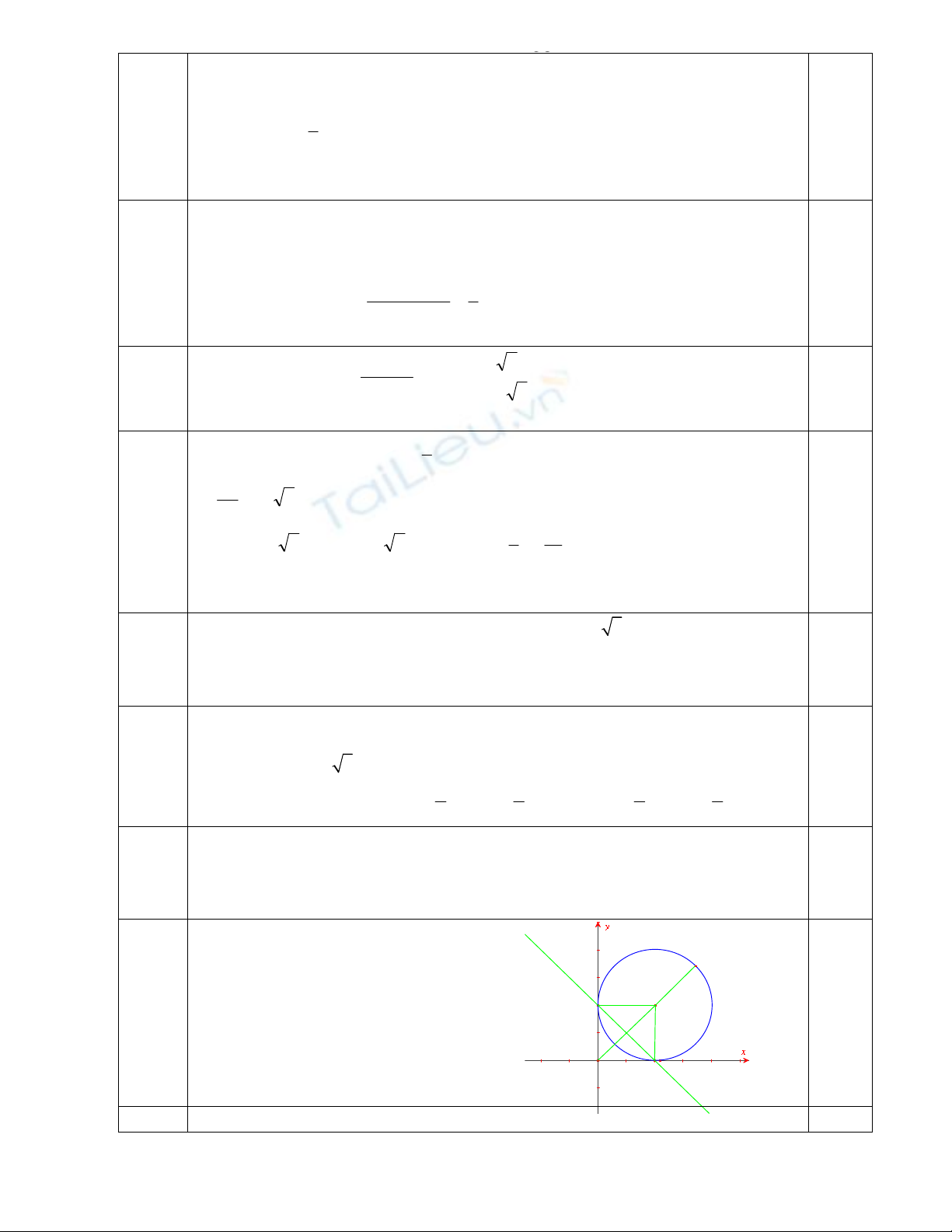0,25 * Ch! ra (C) có tâm I(2;2), R = 2. C *T a giao i m d và (C) là nghi m h : x2 + y 2 − 4 x − 4 y + 4 = 0 I x+ y−2 = 0 1 H Gi i h tìm c A(0;2); B(2;0) 1 Hay d luôn c t (C) t i hai i m phân bi t A và B 0,25
www.VNMATH.com 1 0,25 * Ta có S ∆ABC = AB.CH ( H là hình chi u C trên AB), S ∆ABC max CH max 2 C = ∆ ∩ (C ) D' th y ( ∆ ) có pt: y =x xc > 2 Gi i h tìm ( c C 2 + 2; 2 + 2 ) 0,25 Câu Cho khai tri n: (1 + x + x 2 ) = a 0 + a1x + a 2 x 2 +...+a 24 x 24 . Tính a 4 . 12 9a (1 ) * Xét s h ng t,ng quát c a khai tri n: C12 ( x + x 2 )n . n 0,25 * khai tri n ( x + x 2 ) có s h ng t,ng quát: Cnk x n − k .x 2 k n => s h ng t,ng quát c a khai tri n ã cho có d ng: C12 . Cn x n − k .x 2 k (0 ≤ k ≤ n ≤ 12) . n k * S h ng ch a x4 khi n + k = 4, v i k trên ta tìm c 0,25 ( k , n) ∈ {(0; 4);(1;3);(2; 2)} . 0,25 Thay vào ta c: a4 = 1221 0,25 Câu Trong m t ph ng Oxy, cho tam giác ABC bi t B(2;-1), ng cao và phân 7b giác trong qua nh A và C l n l t có ph ng trình: 3x – 4y + 27 = 0 và (1 ) x + 2y – 5 = 0. Vi t ph ng trình các c nh c a tam giác ABC. * Ph ng trình c nh BC: 4x+3y-5=0 4x + 3y − 5 = 0 *T a C là nghi m h : =>C(-1;3) x + 2y −5 = 0 * G i B' i m i x ng c a B qua CD => B' AC là ∈ 0,5 * Tìm c B' ph ng trình AC: y = 3. => A * Tìm c A(-5;3) * Vi t c pt AB: 4x+7y-1=0. D 0,25 KL: 0,25 H C B Câu Trong m t ph ng Oxy, vi t ph ng trình chính t c c a Elíp (E), bi t r ng 8b 5 (1 ) tâm sai c a (E) b ng và hình ch nh t c s có di n tích b ng 24 3 x2 y 2 Gi s+ ptct (E): + = 1, (a > b > 0) a 2 b2 c a 2 − b2 5 0,5 T) gi thi t ta có e = = = 2a=3b, (1) a a 3 M t khác hình ch nh t c s có chi u dài b ng 2a, chi u r ng 2b nên ta có: 2a.2b= 24 a.b = 6, (2) 0,25 Gi i h (1) và (2) tìm c a = 3, b= 2. x2 y2 0,25 KL: + =1 9 4 Câu M t h p ng 15 viên bi, trong ó có 7 viên bi xanh và 8 viên bi . L y 9b ng u nhiên 3 viên bi (không k th t ra kh i h p). Tính xác xu t trong 3 (1 ) viên bi l y ra có ít nh t 1 viên bi .
www.VNMATH.com * S ph"n t+ không gian m#u: n ( Ω ) = C15 = 455 3 0,25 * Xét A là bi n c "c 3 viên c ch n màu xanh": => n(A) = C73 =35 35 1 0,25 * Xác su t c a bi n c A: P( A) = = 455 13 * Xét B là bi n c "có ít nh t 1 bi c ch n" 0,5 12 P(B) = 1- P(A) = 13 KL: Chú ý: - Trên ây ch là áp án v n t t và h ng d n cho i m. H c sinh ph i l p lu n ch t ch m i cho i m t i a. - H c sinh gi i cách khác úng v n cho i m t i a theo thang i m.

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.