THPT CHUYÊN HÀ NỘI – AMSTERDAM.
KỲ THI TUYỂN SINH ĐẠI HỌC, CAO ĐẲNG NĂM 2013
Môn thi: TOÁN, khối A
Thời gian làm bài 180 phút, không kể thời gian phát đề.
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm):
1. Câu I (2 điểm) :
Cho hàm số
)1()1()1(
22
−+= xxy
, cã ®å thÞ
)( C
.
1) Khảo sát sự biến thiên và vẽ đồ thị
)( C
của hàm số (1) .
2) Lập phương trình đường thẳng
)(d
đi qua điểm cực đại của đồ thị
)( C
sao cho tổng các
khoảng cách, từ hai điểm cực tiểu của đồ thị
)( C
đến đường thẳng
)(d
đạt giá trị lớn nhất.
2. Câu II (2 điểm) :
1) Giải phương trình :
xxx
2
cos8cot2tan =+
.
2) Giải hệ phương trình :
−=−
−=−
3223
2
3
335
yyxx
xyxyx
.
3. Câu III (1 điểm) :
Tính diện tích hình phẳng
)( H
giới hạn bởi các đường
xyP 4:)(
2
=
và
042:)( =−−∆ yx
.
4. Câu IV (1 điểm) :
Cho hình lăng trụ đứng
CBAABC ′′′
.
có đáy (ABC) là tam giác cân với
aACAB ==
,
góc
0
120=∠BAC
, cạnh bên
aBB =
′
, gọi I là trung điểm của
CC ′
. Tính góc giữa hai mặt
phẳng
)(ABC
và
)( IBA ′
5. Câu V (1 điểm) :
Cho hàm số
2
7
12
2
11
)( x
x
xxfy +++==
với
0>x
.Tìm giá trị nhỏ nhất của hàm số .
II. PH
PHPH
PHẦN RI£NG
N RI£NG N RI£NG
N RI£NG (3,0 điểm):Thí sinh chỉ được chọn một trong hai phần riêng (Phần A hoặc phần B)
A.
Theo chương trình chuẩn
:
1. Câu VI.a (1 điểm): Trong mặt phẳng tọa độ 0xy cho tam giác ABC với các đường cao AD, BE, CF.
Biết tọa độ các điểm )2;1( −−D,)2;2(E,)2;1(−F. Viết phương trình các đường thẳng chứa các
cạnh của tam giác ABC.
2. Câu VII.a (1 điểm): Tính tổng :
2013
2013
3
2013
2
2013
1
2013
0
2013
.2014.4.3.2.1 CCCCCS +++++= ⋯
.
3. Câu VIII.a (1 điểm):Trong không gian tọa độ 0xyz cho mặt phẳng
0222:)( =++− zyxP
và các
điểm)3;1;4(A, )1;3;2( −−B. Tìm tọa độ của điểm M nằm trên mặt phẳng (P) sao cho tổng
22
MBMA +
đạt giá trị nhỏ nhất.
B. Theo chương trình nâng cao :
1. Câu VI.b (1 điểm): Trong mặt phẳng tọa độ 0xy cho đường thẳng
024:)( =−− yxd
và tam giác
ABC có điểm A thuộc đường thẳng
)(d
, đường thẳng BC song song với đường thẳng
)(d
, đường
cao BH có phương trình
03 =++ yx
, điểm )1;1(Mlà trung điểm AC.Tính tọa độ các điểm A, B, C.
2. Câu VII.b (1 điểm): Biết rằng
1024
12
12
5
12
3
12
1
12
=++++
+
++++
n
nnnn
CCCC
⋯
. Tìm hệ số của số hạng chứa
7
x
trong khai triển của nhị thức
n
x)43( −.
3. Câu VIII.b (1 điểm):Trong không gian tọa độ 0xyz cho mặt phẳng
0922:)( =+−− zyxP
và mặt
cầu
100)1()2()3(:)(
222
=−+++− zyxS
. Tìm tọa độ của điểm M nằm trên mặt cầu (S) sao cho khoảng
cách từ M đến mặt phẳng (P) đạt giá trị lớn nhất.
……………..…………… Hết .…………………………..
ĐỀ THI THỬ ĐỢT MỘT.
Cảm ơn(hotboy@gmail.com)gửitới www.laisac.page.tl
1
Trường THPT Chuyên Hà nội – Amsterdam
HƯỚNG DẪN CHẤM THI THỬ ĐH-CĐ 2013
Câu Nội dung
ð
i
ểm
C©u I:
C©u I:C©u I:
C©u I:
(
((
(
1.0 ®iÓm
1.0 ®iÓm
1.0 ®iÓm
1.0 ®iÓm
)
) )
) :
: :
:
•
12)1()1(
2422
+−=+−= xxxxy
có TXĐ R
0,25®iÓm
Câu I:
(1.0 ®
(1.0 ®
(1.0 ®
(1.0 ®iÓm
iÓmiÓm
iÓm)
))
)
⇒
0)1(444
23
=−=−=
′xxxy
tại x=0(y=1) và (
1±=x
,y=0)
• (
0412
2
=−=
′′ xy
tại
)
9
4
(,
3
1=±= yx
)
• Đồ thị hàm số không có tiệm cận.
•
+∞==
−∞→+∞→
yy
xx
limlim
• Bảng biến thiên
x
∞−
-1 0 1
∞+
y’ - 0 + 0 - 0 +
y
∞+
∞+
1
0 0
0,25®iÓm
0,25 ®iÓm
0,25®iÓm
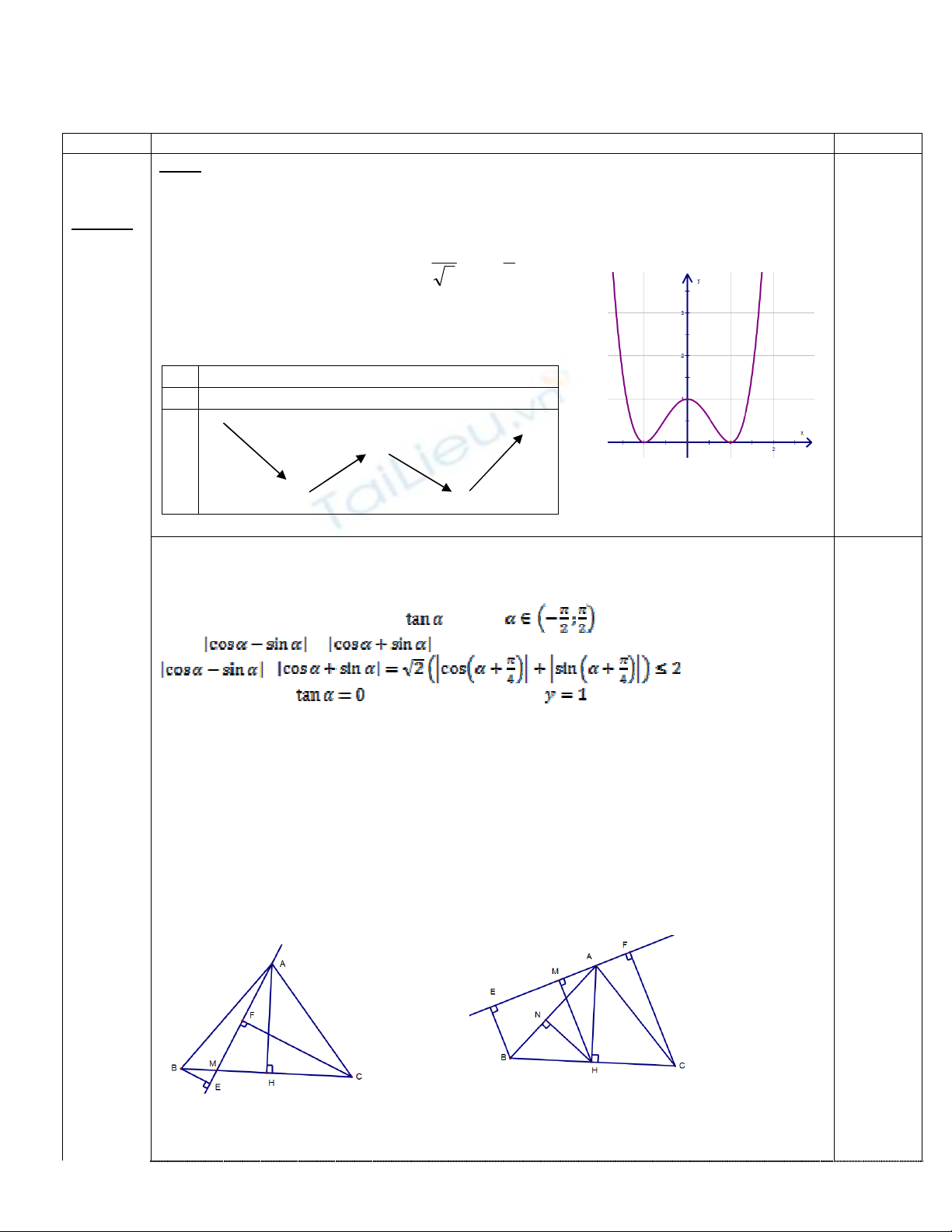
2. Điểm cực đại A(0;1), hai điểm cực tiểu B(-1;0) và C(1;0) tạo thành tam giác cân tại A. Gọi
(d) là đường thẳng qua A
Oyd ≡thì tổng các khoảng cách từ B và C đến (d) bằng BC=2
Oyd ≠thì phương trình (d) là y= .x+1 với . Các khoảng cách từ B và C đến
(d) là: và . Tổng các khoảng cách trên là:
+
Dấu đẳng thức khi nên phương trình (d) là
Vậy có hai đường thẳng thỏa mãn là Oy và y=1
*) Chú ý: Với hàm số trùng phương
cbxaxy ++=
24
khi đồ thị có đủ các điểm cực đại và
cực tiểu thì ba điểm này tạo thành tam giác cân. Ta có bài toán hình học: Cho tam giác ABC
cân ở A, xác định vị trí đường thẳng (d) qua điểm A sao cho tổng các khoảng cách từ hai
đỉnh B và C đến (d) đạt giá trị nhỏ nhất, lớn nhất.
TH1: (d) cắt cạnh BC tại điểm M (lúc đó hai điểm B, C khác phía nhau qua (d)). Ta có:
2(BE+CF).AM=2.S (với S là diện tích tam giác ABC, S không đổi)
*)BE+CF đạt giá trị nhỏ nhất
AM⇔
đạt giá trị lớn nhất
BM ≡⇔
hoặc
CM ≡
, lúc đó
ABd ≡)( hoặc ACd ≡)( . Giá trị nhỏ nhất bằng độ dài đường cao kẻ từ B hoặc C.
*) BE+CF đạt giá trị lớn nhất
AM⇔
đạt giá trị nhỏ nhất
HM ≡⇔
, lúc đó )(dlà đường
cao đỉnh A và giá trị lớn nhất bằng BC
TH2: (d) không cắt cạnh BC (lúc đó B, C nằm cùng phía với (d)). Ta có: BE+CF=2HM là
đường trung bình hình thang. Chú ý:
HAHMHN ≤≤
.
Giá trị nhỏ nhất đạt khi
HNHM ≡
tức là ABd ≡)( hoặc ACd ≡)( . Giá trị nhỏ nhất bằng độ
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
2
dài đường cao kẻ từ B hoặc C (bằng 2HN)
Giá trị lớn nhất đạt khi
HAHM ≡
lúc đó (d)//BC và giá trị lớn nhất bằng 2AH
Kết luận:
o Giá trị nhỏ nhất đạt khi
ABd ≡
)( hoặc
ACd ≡
)(
o Với giá trị lớn nhất thì:
• Tam giác ABC có góc BAC>90
0
thì 2AH<BC. Giá trị lớn nhất là BC đạt khi
AHd ≡
• Tam giác ABC có góc BAC<90
0
thì 2AH>BC. Giá trị lớn nhất là 2AH đạt khi
BCd //
• Tam giác ABC có góc BAC=90
0
thì 2AH=BC. Giá trị lớn nhất là 2AH=BC đạt khi
BCd //
hoặc
AHd ≡
Câu II
(2®iÓm)
(2®iÓm)(2®iÓm)
(2®iÓm)
Câu II:
1) Giải phương trình:
xxx
2
cos8cot2tan
=+
Điều kiện xác định: 0sin,02cos
≠≠ xx
2
1
4sin,0coscos.4sin2cos2cos.cossin8cos
cos8
sin.2cos
cos
cos8
sin
cos
2cos
2sin
cos8cot2tan
2
222
==⇔=⇔=⇔
=⇔=+⇔=+
xxxxxxxxx
x
xx
x
x
x
x
x
x
xxx
Nghiệm
0cos =x
cho
01sin ≠±=x
và 011cos22cos
2
≠−=−= xx
nên thỏa mãn điều
kiện xác định. Ta có nghiệm
π
π
kx += 2
(
Ζ
∈k
).
Nghiệm
2
1
4sin =x
cho
0
2
1
2cos.cos.sin4 ≠=xxx
cũng thỏa mãn điều kiện xác định.
Ta có:
π
π
π
π
2
6
5
4,2
6
4kxkx +=+= Ζ∈+=+=⇔ k
k
x
k
x,
224
5
,
224
π
π
π
π
Chú ý: Nếu biến đổi theo biến
x
ttan=
ta được phương trình:
01828
234
=+−++ tttt
.
Tuy giải được phương trình này nghiệm biểu diễn phức tạp và khó đối chiếu với điều kiện
xác định.
0,25 ®iÓm
0,25 ®iÓm
0,25 ®iÓm
0,25 ®iÓm
C©u
C©u C©u
C©u
I
II
I
I/
2) Giải hệ phương trình:
+=+
+=+
⇔
−=−
−=−
2233
2
3223
2
3
335
3
335
yxyx
yxxyx
yyxx
xyxyx
TH1:
03 =+ yx
cho
.3yx −=
Thay vào hệ có:
0== yx
TH2:
0
22
=+ yx
cho
0== yx
và thỏa mãn hệ
TH3:
≠+
≠+
0
03
22
yx
yx
ta có:
0)94)((
0954)3)(3())(35(
2222
422433222
=+−⇔
=−+⇔++=++
yxyx
yyxxyxyxyxxyx
Trường hợp:
0)94(
22
=+ yx
cho
0== yx
. Nghiệm bị loại vì
0
22
≠+ yx
Trường hợp:
22
yx =
cho
2/1== yx
và
1,1 =−= yx
thỏa mãn điều kiện
Trả lời: Nghiệm
)1,1(),2/1;2/1(),0;0();( −=yx
0,25 ®iÓm
0,25 ®iÓm
0,25 ®iÓm
0,25 ®iÓm
3
Câu III
(2 ®iÓm)
(2 ®iÓm) (2 ®iÓm)
(2 ®iÓm)
C©u
C©u
C©u
C©u
III /
III /III /
III /
Cách 1:
xyP 4:)(
2
=
cắt
042:)( =−−∆ yx
ở
)2;1( −A
và
)4;4(B
,
Từ đồ thị suy ra diện tích cần tìm là:
9.)]42(2[.22
4
1
1
0
=−−+=
∫∫
dxxxdxxS
(đvdt)
Cách 2: Lấy đối xứng qua phân giác góc 1 thì (P):
xy 4
2
=
thành
(P’):
yx 4
2
=
hay
4
2
x
y=
;
042:)( =−−∆ yx
thành
042:)'( =−−∆ xy
hay
2
2+= x
y
(P’) cắt
)'(∆
ở A’(-2;1) và B’(4;4). Từ đồ thị suy ra diện tích
cần tìm là:
9
4
2
2
4
2
2
=
−+=
∫
−
dx
xx
S
(đvdt)
0,5 ®iÓm
0,5 ®iÓm
0,5 ®iÓm
0,5 ®iÓm
Câu IV
(1 điểm)
1/ Có thể đạt hình lăng trụ đứng đã cho vào không gian tọa độ Oxyz với A(0;0;0) trùng gốc
tọa độ O, B(a;0;0),
)0;
2
3
;
2
(aa
C−
, A’(0;0;a),
B’(a;0;a),
−a
aa
C;
2
3
;
2
'
.
Lúc đó
−
2
;
2
3
;
2
aaa
I
.
Mp(ABC) là mặt phẳng xOy có vtpt
1),1;0;0( =kk
' ( ;0; ) (1;0;1)AB a a a= =
,
( )
1;3;1
22
;
2
3
;
2−−
−
=
−aaaa
AI
( )
', 3; 2; 3AB AI u
= − =
là vtpt của mp(AB’I),
10=u
3. −=uk
,
10
3
),cos( −=uk
. Vậy góc nhọn
α
giữa hai mặt phẳng cần tìm có
10
3
cos =
α
0,5 ®iÓm
0,5 ®iÓm
4
Câu V
Cách 1: Theo BĐT Bunhiacopxki cho (1,
x
7
) và
)7,3(
. Ta có:
( )
xxxxxx 2
7
2
37
1.2
7
3
7
14
7
379
7
1
22
2
2
+≥+⇒+≥+⇒
+≥+
+
Từ đó:
2
15
2
39
.2
2
39
2
7
2
3
2
11 =+≥++=+++≥ x
x
x
x
xx
xA
Dấu đẳng thức đạt trong cả hai lần xét BĐT khi x=3, giá trị nhỏ nhất của biểu thức
2
15
=A
Cách 2:
x
x
x
x
xx
xxf 7
.2
2
117
12
2
11
)(
2
2
+
++=+++=
với miền xác định x>0
Có:
()
()
0
7.2
2178247
7.
7
.2
2
11
1)('
22
222
2
2
2
2
≥
+
+++−+
=
+−
+
+−=
xx
xxx
x
xx
x
x
x
xf
347
2
≥⇔≥+⇔ xx
. Vậy GTNN
2
15
)3()( == fxf
khi
3=x
Chú ý: Để xét dấu f’(x) có thể đổi biến
7
2
+= xt
0,25 ®iÓm
0,25 ®iÓm
0,25 ®iÓm
0,25 ®iÓm
0,25 ®iÓm
0,5 ®iÓm
0,25 ®iÓm
VIa Nhận xét với tam giác ABC không vuông có các đường cao AD, BE, CF thì ta có tam giác DEF.
Với tam giác ABC thì AB, BC, CA là các cạnh, còn với tam giác DEF thì AB, BC, CA là các
đường phân giác ngoài (hoặc có hai cạnh là đường phân giác trong, cạnh còn lại là phân giác
ngoài của đỉnh còn lại).
Phương trình đường thẳng DE: ; EF: y – 2 = 0 ; FD: x + 1 = 0.
Phương trình các phân giác trong và ngoài của tam giác DEF đi qua các đỉnh D, E, F lần lượt là
d
1
: 3x – y + 1 = 0 ; d’
1
: x + 3y + 7 = 0 ;
d
2
: x – 2y + 2 = 0 ; d’
2
: ;
d
3
: x + y – 1 = 0 ; d’
3
: x – y + 3 = 0 ;
Trong đó d
1
; d
2
; d
3
là các đường phân giác trong lần lượt tại D, E, F.
d’
1
; d’
2
; d’
3
: là các đường phân giác ngoài lần lượt tại D, E, F.
Đáp số :
Phương trình AB, BC, CA lần lượt là (d’
1
; d’
2
; d’
3
) ; (d
1
; d
2
; d’
3
) ; (d
1
; d’
2
; d
3
) ; (d’
1
; d
2
; d
3
).
H
FE
D
C
B
A
H
BC
D
F
E
A
0,25
0,25
0,25
0,25
VII.a Xét
Ta có
Khi đó S =
0,25
0,25
0,5
VIII.a Lấy E là trung điểm của AB thì E(3 ; -1 ; 1)
Ta có MA
2
+ MB
2
= 2ME
2
+ ; với AB
2
là đại lượng không đổi. Do đó MA
2
+ MB
2
đạt giá trị
nhỏ nhất khi ME nhỏ nhất M là hình chiếu của E trên (P).
Mp(P) có vectơ pháp tuyến (1 ; - 2 ; 2) nên đường thẳng EM đi qua E và vuông góc với (P)
có phương trình tham số . Điểm M ứng với t thoả mãn phương trình mặt
phẳng (P)
(3 + t) – 2( - 1- 2t) + 2(1 + 2t) + 2 = 0 9t + 9 = 0 t = - 1.
0,5
0,5