www.MATHVN.com – Toán học Việt Nam
Dethithudaihoc.com
SỞ GIÁO DỤC & ĐÀO TẠO BÌNH PHƯỚC
TRƯỜNG THPT HÙNG VƯƠNG
ĐỀ THI THỬ ĐẠI HỌC LẦN 3 NĂM 2014
Môn thi: TOÁN – Khối A, A
1
, B
Thời gian làm bài: 180 phút
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)
Câu 1 (2,0 điểm). Cho hàm số
(
)
3
3 2
y x x C
= − +
a) Khảo sát sự biến thiên và vẽ đồ thị
(
)
C
của hàm số đã cho;
b) Tìm tất cả các giá trị
m
để đường thẳng
( ) : 2 4
= − +
cắt đồ thị
(
)
C
tại ba điểm phân
biệt
(
)
2, 4
A,
,
B C
sao cho tam giác
OBC
cân tại
O
, với
O
là gốc tọa độ.
Câu 2 (2,0 điểm). Giải các phương trình, hệ phương trình
a)
sin 2 cos 2 2 2 cos 1
x x x
− = +
b)
( )
2
2
2
2 2
2
0
1,
2 1 3
y
x y
x x x y
xx y
y
+ + =
+ + ∈
+ + + =
R
Câu 3 (1,0 điểm). Tính tích phân
( )
2
2
0
sin sin
I x x x dx
π
= +
∫
Câu 4 (1,0 điểm). Cho lăng trụ
. ' ' '
ABC A B C
có tam giác
ABC
vuông tại
B
,
, 2
AB a BC a
= =
. Hình
chiếu của
'
A
trên mặt phẳng
( )
ABC
là trung điểm
H
của
BC
, cạnh bên
'
A A
hợp với đáy góc
45
o
.
Tính thể tích khối lăng trụ
. ' ' '
ABC A B C
và khoảng cách từ
C
đến mặt phẳng
(
)
' '
AA B B
.
Câu 5 (1,0 điểm). Tìm
m
để phương trình sau có nghiệm duy nhất trên
1
;1
2
−
2 3 2
3 1 2 2 1
x x x m
− − + + =
II. PHẦN RIÊNG (3,0 điểm) Thí sinh chỉ được làm một trong hai phần ( A hoặc B)
A. Theo chương trình Chuẩn
Câu 6.a (1,0 điểm). Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
có trung tuyến
: 2 0
AI x y
+ − =
, đường cao
: 2 4 0
AH x y
− + =
và trọng tâm
G
thuộc trục hoành. Tìm tọa độ của
B
và
C
; biết
(
)
5; 1
E
−
thuộc đường cao qua
C
.
Câu 7.a (1,0 điểm). Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
(
)
(
)
1;1;2 , 1;3; 2
A B
− −
và đường
thẳng
1 2
:
1 2 1
x y z
d
− +
= =
− −
. Tìm điểm
I
trên
d
sao cho tam giác
IAB
cân tại
I
, viết phương trình
mặt cầu đi qua hai điểm
,
A B
và có tâm thuộc đường thẳng d.
Câu 8.a (1,0 điểm). Tìm số phức
z
thỏa mãn
(
)
2
3 4 1 5 7
z z z i
− − + = +
B. Theo chương trình Nâng cao
Câu 6.b (1,0 điểm). Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác ABC có
(
)
1;6
A
, trực tâm
(
)
1;2
H
,
tâm đường tròn ngoại tiếp
(
)
2; 3
I
. Tìm tọa độ
,
B C
; biết B có hoành độ dương.
Câu 7.b (1,0 điểm). Trong không gian
Oxyz
cho mặt cầu
(
)
2 2 2
: 2 4 6 0
S x y z x y z
+ + − + − =
và
đường thẳng
2 1 1
:
1 1 1
x y z
− − −
∆ = =
−
. Tìm tọa độ giao điểm của
∆
và
(
)
S
, viết phương trình mặt phẳng
(
)
P
chứa đường thẳng
∆
và tiếp xúc với mặt cầu
(
)
S
.
www.MATHVN.com – Toán học Việt Nam
Dethithudaihoc.com
Câu 8.b (1,0 điểm). Cho số phức
z
thỏa
(
)
1
i z z i
+ + =
. Tìm môđun của số phức
1
i z
ω
= + +
.
. . . . Hết . . . .
www.MATHVN.com – Toán học Việt Nam
Dethithudaihoc.com
SỞ GIÁO DỤC & ĐÀO TẠO BÌNH PHƯỚC
Trường THPT Hùng Vương ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
ĐỀ THI THỬ ĐẠI HỌC LẦN 3 NĂM 2014
Môn thi: Toán; Khối: A, A
1
, B
Đáp án Điểm
Câu 1.a. Cho hàm số
3
3 2
y x x
= − +
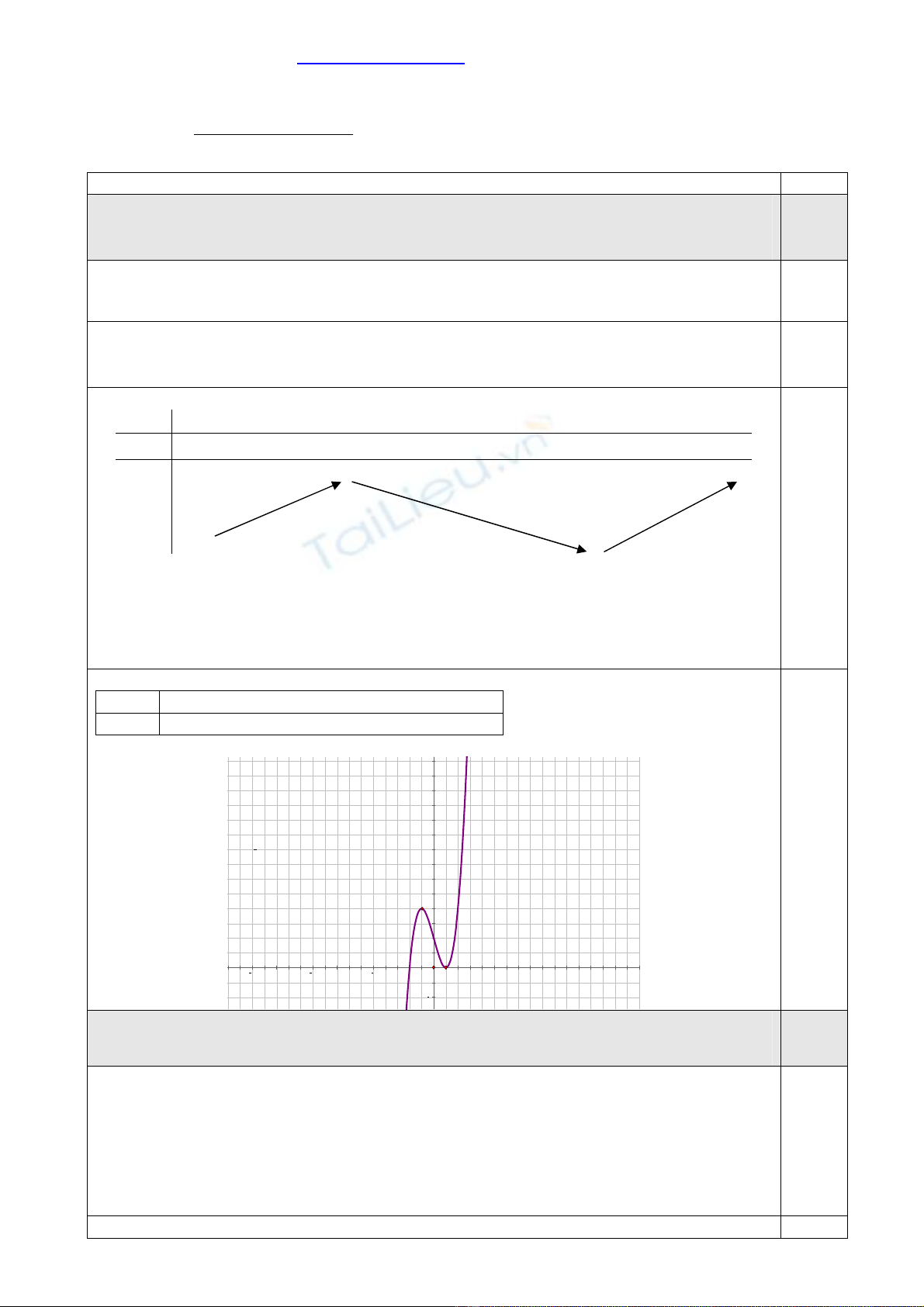
Khảo sát sự biến thiên và vẽ đồ thị
(
)
C
hàm số đã cho;
Tập xác định D = R .
+ Giới hạn:
lim ; lim
x x
y y
→−∞ →+∞
= −∞ = +∞
+
2
' 3 3
y x
= −
;
1
' 0
1
x
yx
=
= ⇔
= −
+ Bảng biến thiên
x
−∞
1
−
1
+∞
'
y
+
0
−
0
+
y
−∞
4
0
+∞
Hàm số đồng biến trên các khoảng
( ; 1)
−∞ −
và
(1; )
+∞
Hàm số nghịch biến trên khoảng
( 1;1)
−
;
Hàm số đạt cực đại tại điểm x =
1
−
, y = 4.
Hàm số đạt cực tiểu tại điểm điểm
1
x
=
, y = 0.
Đồ thị hàm số đi qua các điểm đặc biệt:
x
2
−
1
−
0 1 2
y 0 4 2 0 4
14
12
10
8
6
4
2
2
15 10 5 5 10 15
f x
( )
= x
3
3·x + 2
Câu 1.b. Tìm m để đường thẳng
( ) : 2 4
= − +
cắt
(
)
C
tại ba điểm phân biệt A,
B, C sao cho A cố định và tam giác OBC cân tại O, với O là gốc tọa độ.
Ta có
( ) : 2 4
= − +
Phương trình hoành độ giao điểm của (d) và ( C) là:
3
3 2 2 4
x x mx m
− + = − +
(
)
(
)
2
2
2 2 1 0
2
( ) 2 1 0 (1)
x x x m
x
f x x x m
⇔ − + + − =
=
⇔= + + − =
(d) cắt ( C) tại ba điểm phân biệt khi và chỉ khi phương trình (1) có ba nghiệm phân biệt
www.MATHVN.com – Toán học Việt Nam
Dethithudaihoc.com
khác 2
' 0 0
(2) 0 9
m
f m
∆ > >
⇔
≠ ≠
Ta có
(
)
2; 4
A
, gọi
(
)
(
)
1 1 2 2
; 2 4 , ; 2 4
B x mx m C x mx m
− + − +
theo Vi-et ta có
1 2
1 2
2
. 1
x x
x x m
+ = −
= −
Tam giác OBC cân tại O
( ) ( )
( )
( )
2 2
2 2
2 2
1 1 2 2
2
1 2
2
2 4 2 4
3 4 1 0
1
3 4 1 0 1
3
OB OC
x mx m x mx m
x x m m
m
m m m
⇔ =
⇔ + − + = + − +
⇔ − − + =
=
⇔ − + = ⇔ =
Câu 2.1. Giải phương trình:
sin 2 cos 2 2 2 cos 1
x x x
− = +
( )
2
sin 2 cos 2 2 2 cos 1
2 sin cos 2 cos 2 2 cos 0
2 cos sin cos 2 0
cos 0
cos 0
sin 1
sin cos 2 4
2
32
4
x x x
x x x x
x x x
x
x
x
x x
x k
x k
π
ππ
ππ
− = +
⇔ − − =
⇔ − − =
=
=
⇔ ⇔
− =
− −
= +
⇔
= +
Câu 2.b Giải hệ phương trình:
2
2
2
2 2
2
0
1
2 1 3
y
x y
x x
xx y
y
+ + =
+ +
+ + + =
Điều kiện:
0
y
≠
Ta có hệ :
2 2
2
2 2
2
( 1 ) 0
2 1 3
x y x x y
xx y
y
+ + − + =
+ + + =
2
2
2 2
2
1 0 (*)
2 1 3 (**)
xy x x
y
xx y
y
+ + + − =
⇔
+ + + =
Trừ vế theo vế phương trình (**) cho 2 lần phương trình (*) ta có:
2 2
2 2
2 2
2 2
2 2 3 2 2 3
x x x x
y y x x y y
y y
y y
⇔ − + − + = ⇔ + + − − =
2
2 3 0
x x
y y
y y
⇔ + − + − =
1
3
xy
y
xy
y
+ = −
⇔+ =
www.MATHVN.com – Toán học Việt Nam
Dethithudaihoc.com
Trường hợp 1:
1
x
y
y
+ = −
, thay vào (*) ta có
2
1 1 0
x x
− + + − =
2
1 1 0
x x x
⇔ + = + ⇔ =
, với x = 0 ta có y = 1.
Trường hợp 2:
3
x
y
y
+ =
ta có hệ phương trình:
22
33
1 0
1 3
xx
yy
yy
xy x x x x
y
+ =
+ =
⇔
+ + + − =
+ = −
(vô nghiệm).
Kết luận: Hệ phương trình có một nghiệm là:
(
)
0; 1
−
.
Câu 3 (1,0 điểm). Tính tích phân
( )
2
2
0
sin sin
I x x x dx
π
= +
∫
.
2 2
3
0 0
sin sin
I x x dx x dx
π π
= +
∫ ∫
• Xét
2
0
sin
M x x dx
π
=
∫
, đặt
sin cos
u x du dx
dv xdx v x
= =
⇒
= = −
2
2 2
0 0
0
cos cos 0 sin 1
M x x x dx x
π
π π
= − + = + =
∫
•
( ) ( )
2 2 2 32
3 2 2
0 0 0
0
cos 2
sin 1 cos sin cos 1 (cos ) cos
3 3
x
N x dx x x dx x d x x
π π π π
= = − = − = − =
∫ ∫ ∫
Vậy
2 5
1
3 3
I M N
= + = + =
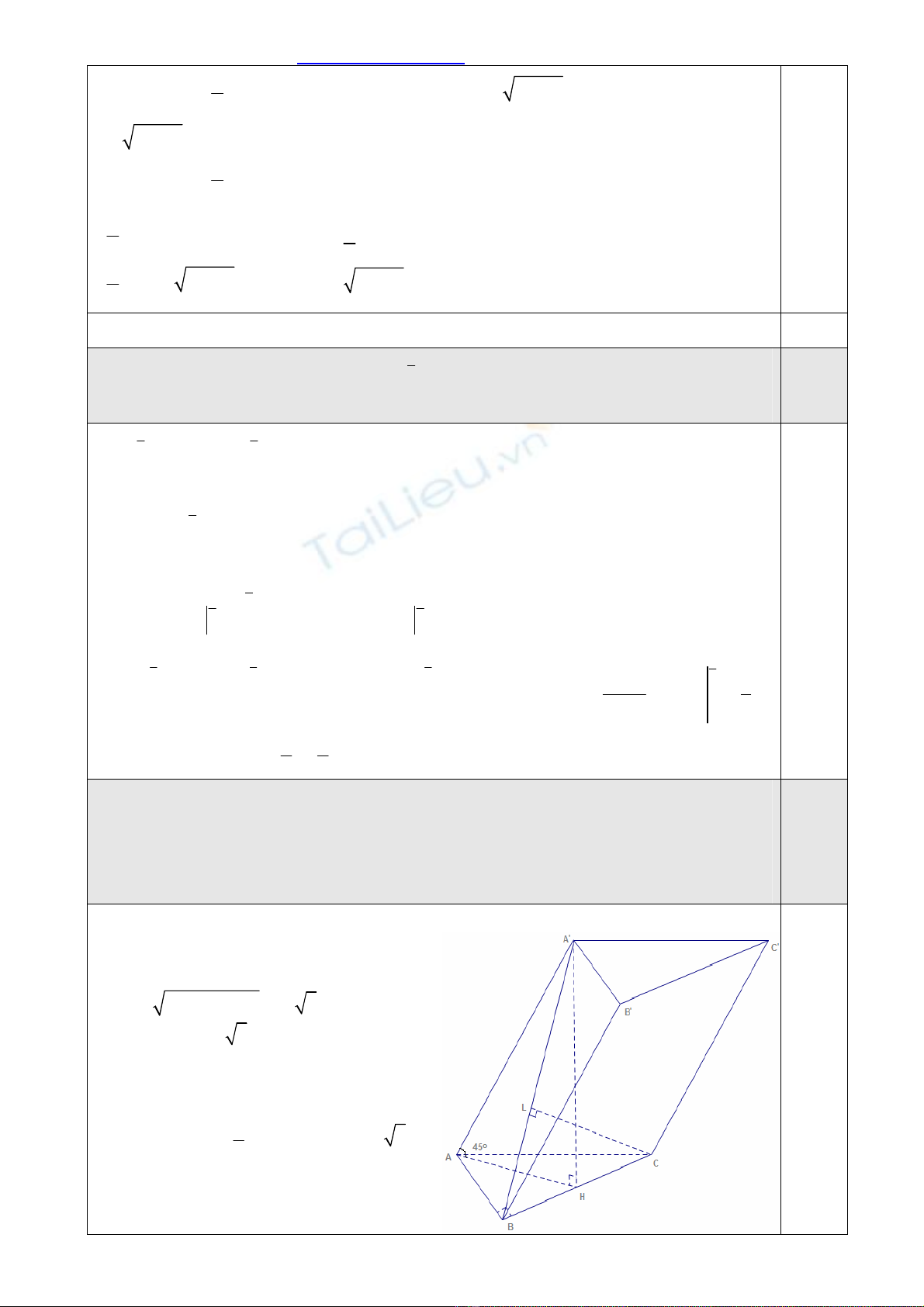
Câu 4 (1,0 điểm). Cho lăng trụ
'''
.
ABC ABC
có tam giác
ABC
vuông tại
B
,
, 2
AB a BC a
= =
. Hình chiếu của
'
A
trên mặt phẳng
( )
ABC
là trung điểm
H
của BC,
cạnh bên hợp với đáy góc
45
o
. Tính thể tích của lăng trụ
'''
.
ABC ABC
và khoảng cách từ
C
đến mặt phẳng
(
)
' '
AAB B
.
Ta có:
(
)
' '
45
o
AH ABC AAH⊥ ⇒ =
BH a
=
,
2 2
2
AH AB BH a
= + =
•
'
2
AH AH a
= =
• Thể tích lăng trụ
' ' 3
1
. . . 2
2
ABC
V S A H AB BC A H a
= = =
(đvtt)
• Gọi L là hình chiếu của C trên