1
SỞ GD&ĐT NGHỆ AN
TRƯỜNG THPT PHAN ĐĂNG LƯU ĐỀ THI THỬ ĐẠI HỌC LẦN I NĂM HỌC 2012−
−−
−2013
MÔN: TOÁN − KHỐI A, B
Thời gian làm bài: 180 phút.
I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)
Câu 1 (2 điểm). Cho hàm số
3 2
1
3
y x x
= − .
1)
Kh
ả
o sát và v
ẽ
đồ
th
ị
(C) c
ủ
a hàm s
ố
;
2)
Vi
ế
t ph
ươ
ng trình ti
ế
p tuy
ế
n c
ủ
a (C) bi
ế
t ti
ế
p tuy
ế
n
đ
ó c
ắ
t các tr
ụ
c Ox, Oy t
ươ
ng
ứ
ng t
ạ
i A, B
phân bi
ệ
t th
ỏ
a mãn OB = 3OA.
Câu 2
(1
đ
i
ể
m). Gi
ả
i ph
ươ
ng trình:
0
cos
6
)
sin2
(tan
tan
3
=
+
+
−
x
x
x
x
Câu 3 (1 điểm). Giải hệ phương trình:
2 2
1 2 2
1 2 3 3
y x
x y
x
y x x x
+ = +
+ = + +
Câu 4 (1 điểm). Tính tích phân
2
2
sin cos
3 sin 2
x x
I dx
x
π
π
−
+
=+
∫
.
Câu 5 (1 điểm). Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, mặt bên SAB là tam giác
đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm SC. Tính thể tích khối chóp
S.ABM và khoảng cách giữa hai đường thẳng SA, BC.
Câu 6 (1 điểm). Cho a,b, c là các số thực không âm thỏa mãn a
2
+ b
2
+ c
2
= 1. Chứng minh:
1
1 1 1
a b c
bc ca ab
+ + ≥
+ + + .
II. PHẦN RIÊNG (3,0 điểm): Thí sinh chỉ được làm một trong hai phần (phần A hoặc phần B).
A. Theo chương trình Chuẩn
Câu 7a (1 điểm). Trong mặt phẳng Oxy cho ∆ABC vuông tại B, AC = 2. Đường phân giác trong của
góc A có phương trình (d): 3 0
x y
− = . Tìm toạ độ các đỉnh A, C biết rằng khoảng cách từ C đến
(d) bằng hai lần khoảng cách từ B đến (d); C nằm trên trục tung và A có hoành độ dương.
Câu 8a (1 điểm). Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:
3
6 5
2
x
y t
z t
= −
= − +
= −
, mặt phẳng
(P): x + 2y − 2z + 4 = 0 và điểm A(−3; −1; 2). Viết phương trình mặt phẳng (α) đi qua A, vuông góc
với (P) và cắt d tại điểm M thỏa mãn: khoảng cách từ M đến (P) bằng MA.
Câu 9a (1 điểm). Tìm hệ số của x
6
trong khai triển (x
2
+ x – 2)
n
, biết n là số nguyên dương thỏa mãn:
2 3
0 1 2 3
2 2 2 121
...
3 4 1 1
nn
n n n n n
C C C C C
n n
+ + + + + =
+ + .
B. Theo chương trình Nâng cao
Câu 7b (1 điểm). Trong mặt phẳng Oxy cho elip (E):
22
1
4
xy
+ = và 2 điểm ( 3;0), ( 3;0)
A B
−.
Tìm điểm M thuộc (E) sao cho
0
60
AMB =.
Câu 8b (1 điểm). Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: 1 2
2 1 1
x y z
+ −
= = , mặt
phẳng (P): x + y − 2z + 5 = 0 và điểm A(1; −1; 2). Viết phương trình đường thẳng ∆ đi qua A song
song với mặt phẳng (P), đồng thời vuông góc với d.
Câu 9b (1 điểm).
Gi¶i ph−¬ng tr×nh:
( ) ( )
2
2 2
log log
3 1 . 3 1 1
x x
+ + − = +
.
Cảmơnlovemath@gmail.comgửitới www.laisac.page.tl
2
…………………………. Hết …………………………
ĐÁP ÁN ĐỀ THI THỬ ĐẠI HỌC LẦN 1. NĂM HỌC 2012 −
−−
− 2013
Câu Nội dung Điểm
1
(2 điểm)
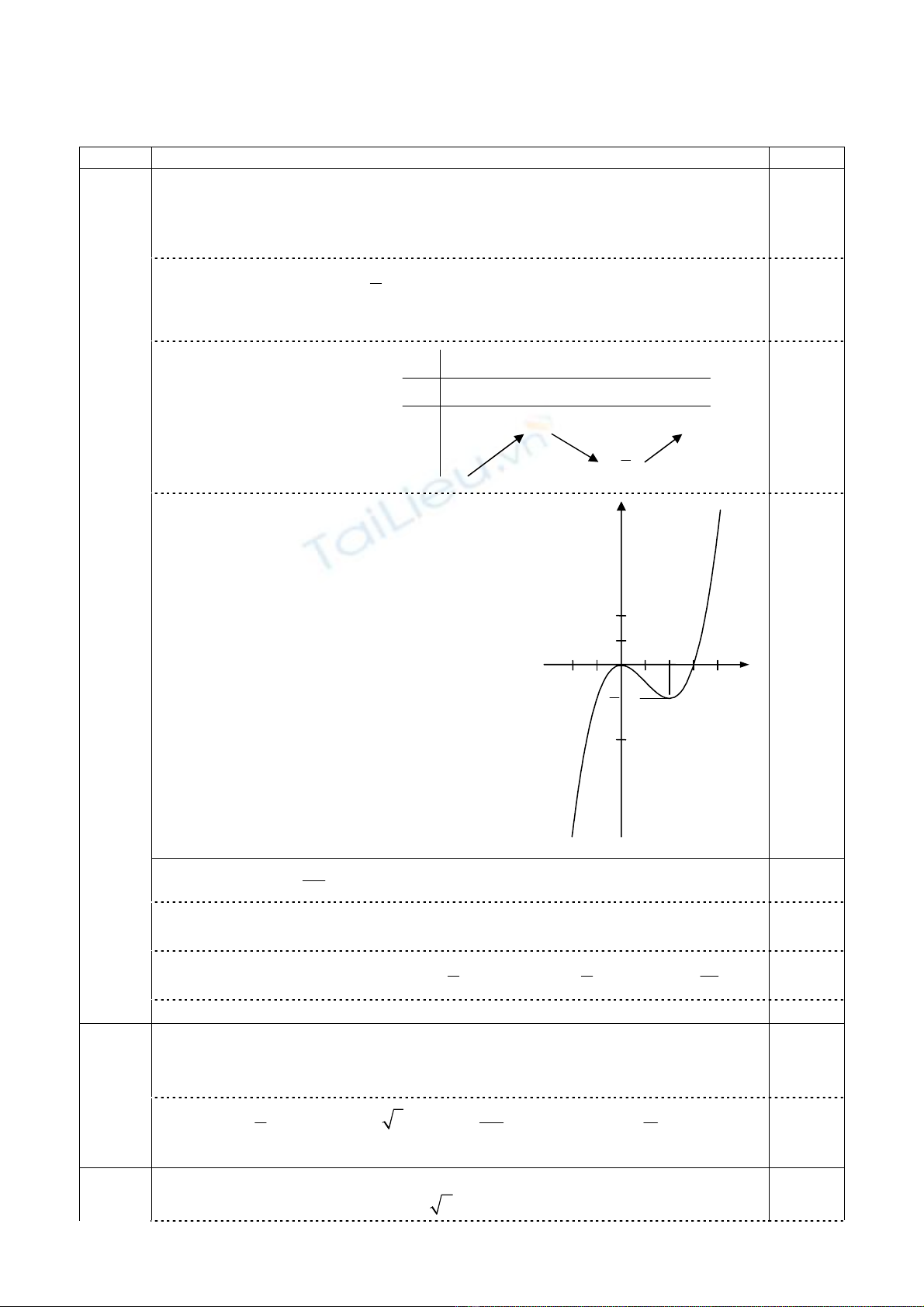
1) • TXĐ:
ℝ
.
• SBT:
− CBT: y’ = x
2
− 2x = 0 ⇔ x = 0 hoặc x = 2
Hàm số ĐB trên (−∞; 0) và (2; +∞); hàm số NB trên (0; 2).
0,25
− Cực trị: CĐ(0;0); CT(
4
2; 3
−
).
− Gi
ớ
i h
ạ
n:
lim
x
y
→−∞
= −∞
, lim
x
y
→+∞
= +∞ .
0,25
− BBT:
0,25
•
Đồ
th
ị
0,25
2) Ta có:
tan 3
OB
OAB OA
= =
⇒
h
ệ
s
ố
góc c
ủ
a ti
ế
p tuy
ế
n là ±3.
0,25
G
ọ
i x0 là hoành
độ
ti
ế
p
đ
i
ể
m thì
y’(x0) = ±3 ⇔ 2
0 0
2 3
x x
− = ±
⇔ x0 = −1 ho
ặ
c x0 = 3.
0,25
• PT ti
ế
p tuy
ế
n c
ủ
a (C) t
ạ
i
đ
i
ể
m ( 4
1; 3
− − ): 4
3( 1) 3
y x
= + + hay 13
33
y x
= + .
0,25
• PT ti
ế
p tuy
ế
n c
ủ
a (C) t
ạ
i
đ
i
ể
m (3; 0): y = 3(x − 3) hay y = 3x − 9.
0,25
2
(1
đ
i
ể
m)
Đ
K: cosx ≠ 0.
⇔
2
3(1 2cosx) tan x(1 2cos x) 0
+ − + =
⇔ (1 + 2cosx)(3 − tan2x) = 0
0,5
⇔ 1
cos 2
x
= − ho
ặ
c tan 3
x
= ± ⇔ 22
3
x k
π
π
= ± + ho
ặ
c 3
x k
π
π
= ± + .
Đố
i chi
ế
u
Đ
K, ph
ươ
ng trình có các nghi
ệ
m trên.
0,5
3
(1
đ
i
ể
m)
Đ
KX
Đ
: x > 0, y ≠ 0.
PT
đầ
u c
ủ
a h
ệ
⇔ y = 2x ho
ặ
c
y x= −
.
0,25
1
2
3
4
3
−
O
x
y
−
3
x
y’
y
−
∞
+
∞
0
2
0
0
+
−
+
0
4
3
−
−
∞
+
∞
3
• Với y = 2x, ta có:
2 2
2 1 2 3 3
x x x x
+ = + +
(*) ⇔
2
1 3
12
1
x
x
= +
+.
0,25
Dễ thấy hàm số
2
1 3
( ) 2
1
f x
x
x
= +
+ nghịch biến trên (0; +∞).
Mặt khác ( 3) 1
f=
Vậy (*) có nghiệm dy nhất 3x= ⇒ 2 3y=.
0,25
• Với y x= − ta có:
2 2
1 2 3 3
x x x x
− + = + +
: PT này vô nghiệm vì vế trái
không dương, vế phải dương.
Tóm lại hệ có nghiệm duy nhất 3x=; 2 3y=.
0,25
4
(1 điểm)
2 2
2
2 2
sin cos sin cos
3 sin 2 4 (sin cos )
x x x x
I dx dx
x x x
π π
π π
− −
+ +
= =
+ − −
∫ ∫
0,25
Đặt sinx − cosx = t, ta có:
1 1
2
1 1
1 1 1
4 4 2 2
dt
I dt
t t t
− −
= = +
− + −
∫ ∫
0,5
=
1
1
1(ln | 2 | ln | 2 |)
4t t
−
+ − − = 1ln3
2.
0,25
5
(1
đ
i
ể
m)
• Do M là trung
đ
i
ể
m SC nên
1
( ,( )) ( ,( ))
2
d M SAB d C SAB
=
⇒
1
2
SABM SABC
V V
=.
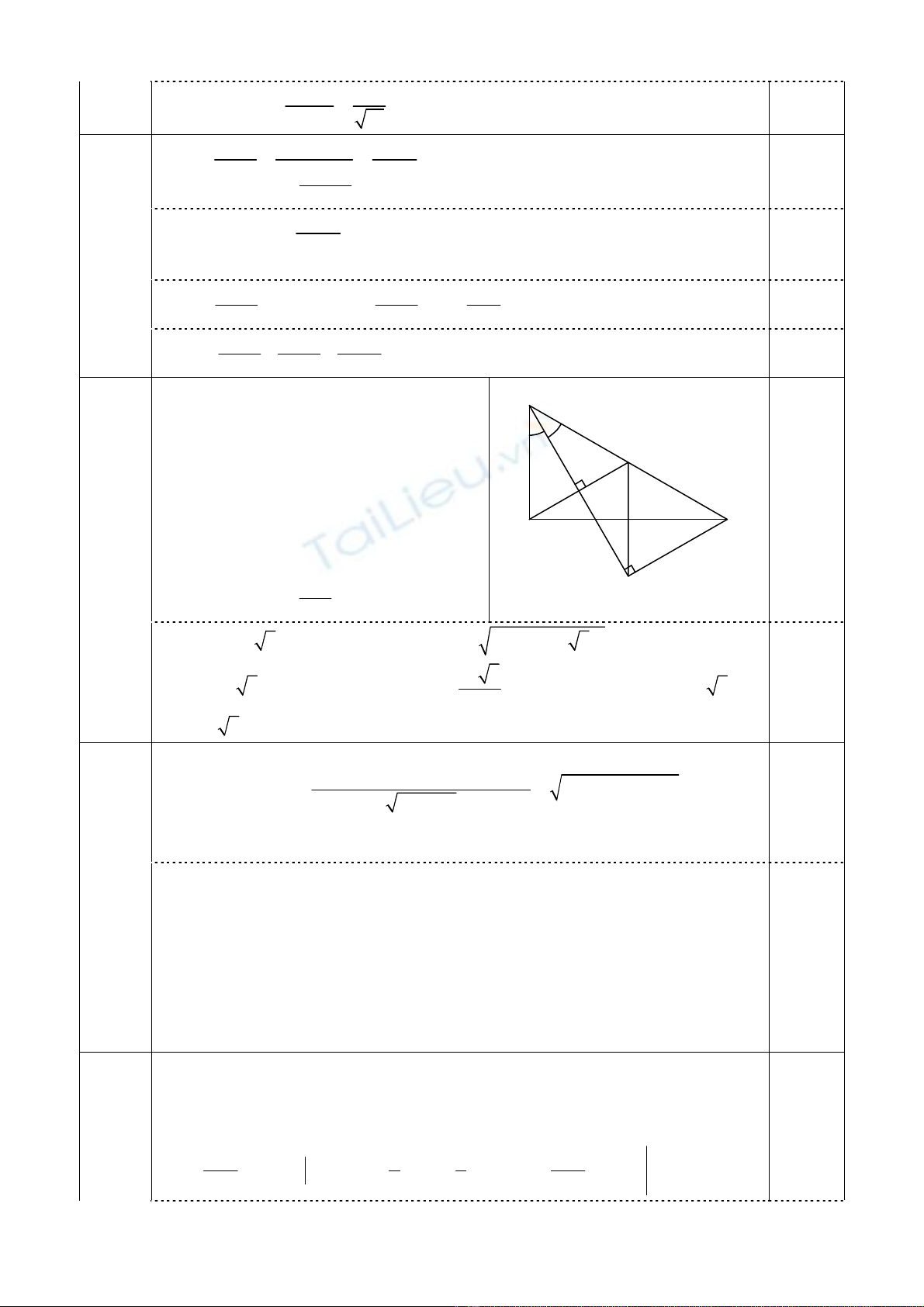
Vì (SAB) ⊥ (ABC) nên g
ọ
i SH là
đườ
ng
cao c
ủ
a ∆SAB thì SH ⊥ (ABC)
∆SAB
đề
u c
ạ
nh a
⇒
3
2
a
SH =.
0,25
2 3
1 1 3 3
.
3 3 2 4 8
SABC ABC
a a a
V SH S
= = =
V
ậ
y
3
16
SABM
a
V=
.
0,25
• G
ọ
i D là
đ
i
ể
m sao cho ACBD là hình bình hành
⇒
(SAD) ch
ứ
a SA và song
song BC
⇒
d(SA, BC) = d(BC, (SAD)) = d(B, (SAD))= 3
SABD
SAD
V
S.
Ta có:
3
8
SABD SABC
a
V V
= =
.
∆SHC vuông cân t
ạ
i H
⇒
6
22
a
SC SH= = .
BM là
đườ
ng cao tam giác cân SBC
⇒
BM =
2
2 2 2
6 10
4 4
a a
SA SM a
− = − =
.
0,25
2
1 1 10 6 15
. . .
2 2 4 2 8
SAD SBC
a a a
S S BM SC
= = = =
0,25
S
D
A
H
B
C
M
4
⇒ d(SA, BC) =
33
15
SABD
SAD
Va
S=.
6
(1
đ
i
ể
m)
Ta có:
2 2 2
2
1 3
12
a a a
b c
bc a
≥ =
+
+ −
+
.
0,25
M
ặ
t khác d
ễ
th
ấ
y
2
2
2
3
aa
a≥
− (*).
Th
ậ
t v
ậ
y (*)
⇔
a(a
−
1)
2
(a + 2)
≥
0 luôn
đ
úng.
0,25
Suy ra
2
1
aa
bc
≥
+
, t
ươ
ng t
ự
2
1
bb
ca
≥
+
,
2
1
cc
b
≥
+
.
0,25
Do
đ
ó:
2 2 2
1
1 1 1
a b c a b c
bc ca ab
+ + ≥ + + =
+ + +
(
đ
pcm).
0,25
7a
(1
đ
i
ể
m)
G
ọ
i M là
đ
i
ể
m
đố
i x
ứ
ng c
ủ
a B qua d
⇒
M
∈
AC.
G
ọ
i H, K l
ầ
n l
ượ
t là hình chi
ế
u c
ủ
a C, B
trên d.
Vì CH = 2BK nên CH = BM = 2KM
⇒
M
là trung
đ
i
ể
m AC.
Vì các tam giác ABC, AHC vuông c
ạ
nh
huy
ề
n AC nên MH = MB = MC = HC = 1.
Gi
ả
s
ử
C(0; y
0
)
⇒
CH = d(C,d) =
0
| | 1
2
y
=
⇔
y
0
= ±2.
0,5
Gi
ả
s
ử
( ; 3)
A t t ∈ d (t > 0). Ta có:
2 2
0
( 3) 2AC t y t
= + − =
⇔
20
4 2 3 0
t y t
− =
(do
2
0
4y=) ⇔
0
3
2
y
t=. Vì t > 0 nên y
0
= 2 và 3t=.
Vậy ( 3;3)A, C(0; 2).
0,5
8a
(1 điểm)
Giả sử M(−3; −6 + 5t; 2 − t) ∈ d. ta có:
d(M, (P)) = MA ⇔
2 2
| 3 2( 6 5 ) 2(2 ) 4 | 0 (5 5)
1 4 4
t t t t
− + − + − − + = + − +
+ +
⇔ (4t − 5)
2
= 26t
2
− 50t + 25 ⇔ 10t
2
+ 10t = 0 ⇔ t = 1 hoặc t = 0.
⇒ M(−3; −1; 1) hoặc M(−3; − 6; 2).
0,5
Mặt phẳng (α) cần tìm đi qua M, A và vuông góc với (P) nên có 1 vec tơ pháp
tuyến là [ , ]
p
n MA n
α
=
, với
p
n
là 1 vec tơ pháp tuyến của (P).
• M(−3; −1; 1): Ta có (0;0;1)
MA =
, (1;2; 2)
p
n= −
⇒ ( 2;1;0)
n
α
= −
Phương trình mp (α): −2x + y − 5 = 0.
• M(−3; − 6; 2): (0;5;0)
MA =
, (1;2; 2)
p
n= −
⇒ ( 10;0; 5)
n
α
= − −
⇒ (α): 2x + z + 4 = 0.
Vậy có 2 mặt phẳng thỏa mãn là (α): −2x + y − 5 = 0 và (α): 2x + z + 4 = 0.
0,5
9a
(1 điểm)
Từ khai triển
0 1 2 2
(1 ) ...
nn n
n n n n
x C C x C x C x
+ = + + + + ta có:
2 2 0 1 2 2
0 0
(1 ) ( ... )
n n n
n n n n
x dx C C x C x C x dx
+ = + + + +
∫ ∫
Hay:
2
2
1 0 1 2 2 3 1
00
1 1 1 1
(1 ) ...
1 2 3 1
nn n
n n n n
x C x C x C x C x
nn
++
+ = + + + +
++
0,5
B
H
C
M
K
A
5
⇔
1 2 3 1
0 1 2
3 1 2 2 2
2 ...
1 2 3 1
nnn
n n n n
C C C C
n n
++
−= + + + +
+ +
Kết hợp giả thiết suy ra:
1
3 1 242
1 1
n
n n
+
−=
+ + ⇔ 3
n + 1
= 243 = 3
5
⇔ n = 4.
Ta có (x
2
+ x – 2)
4
= (x − 1)
4
(x + 2)
4
=
0 1 2 2 3 3 4 4 0 1 2 2 3 3 4 4
4 4 4 4 4 4 4 4 4 4
( )( .2 .4 .8 .16 )
C C x C x C x C x C C x C x C x C x
− + − + + + + +
Vậy hệ số x
6
là:
2 4 3 3 4 2
4 4 4 4 4 4
. .16 . .8 . .4 8
C C C C C C
− + = − .
0,5
7b
(1 điểm)
Vì A, B chính là các tiêu điểm (E) nên ta có:
2 2 2 0 2
1
2 . .cos60 ( ) 2 . 2 . .2
AB MA MB MA MB MA MB MA MB MA MB
= + − = + − −
=
2 2
4 3 . 4 3( )( )
a MA MB a a ex a ex
− = − + − =
2 2 2
3
a e x
+
⇒
2
2 2 2
2
4 3 c
c a x
a
= + ⇔
2 2 2
2
2
(4 ) (4.3 4).4 32
3 3.3 9
c a a
xc
− −
= = =
⇒
4 2
3
x= ± .
0,5
Vì M ∈ (E)
⇒
2
2
8 1 1
1 1
4 9 9 3
x
y y
= − = − =
⇒
= ± .
V
ậ
y có 4
đ
i
ể
m th
ỏ
a mãn v
ớ
i t
ọ
a
độ
là
4 2 1
;
3 3
± ±
.
0,5
8b
(1
đ
i
ể
m)
Véc t
ơ
ch
ỉ
ph
ươ
ng và véc t
ơ
pháp tuy
ế
n c
ủ
a d và (P) t
ươ
ng
ứ
ng là
(2;1;1), (1;1; 2)
d p
u n
= = −
.
0,25
G
ọ
i
u∆
là vec t
ơ
ch
ỉ
ph
ươ
ng c
ủ
a ∆, t
ừ
gi
ả
i thi
ế
t suy ra
u∆
vuông góc v
ớ
i các
véc t
ơ
,
d p
u n
⇒ có th
ể
ch
ọ
n [ , ] ( 3;5;1)
d p
u u n
∆
= = −
.
0,5
V
ậ
y ph
ươ
ng trình ∆ là: x = 1 − 3t; y = −1 + 5t; z = 2 + t.
0,25
9b
(1
đ
i
ể
m)
ĐKXĐ: x > 0.
Đặ
t
22
log log
( 3 1) 0,( 3 1) 0
x x
u v
+ = ≥ − = ≥
⇒ u.v = x.
Ta có ph
ươ
ng trình:
u + uv2 = 1 + u2v2 ⇔ (u − 1)( 1 − uv2) = 0 ⇔ u = 1 ho
ặ
c uv2 = 1.
0,5
• u = 1 ⇒ log2x = 0 ⇔ x = 1 (th
ỏ
a mãn PT).
• uv2 = 1 ⇒
2
log
(2 3 2) 1
x
− = ⇔ log2x = 0 ⇔ x = 1 (th
ỏ
a mãn PT).
V
ậ
y PT có nghi
ệ
m duy nh
ấ
t x = 1.
0,5
Lưu ý
:
H
ướ
ng d
ẫ
n này ch
ỉ
trình bày m
ộ
t cách gi
ả
i, n
ế
u h
ọ
c sinh gi
ả
i cách khác mà v
ẫ
n
đ
úng thì cho
đ
i
ể
m t
ố
i
đ
a dành cho ph
ầ
n
đ
ó (ho
ặ
c ý
đ
ó).
Cảmơnlovemath@gmail.comgửitới www.laisac.page.tl