Trang 1/6 - Mã đề thi 132
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2018 LẦN 2
Môn: TOÁN Lớp 12;
(Thời gian 90 phút, không kể thời gian giao đề)
Họ, tên thí sinh: ..................................................................... SBD: …………………… Phòng: .........….
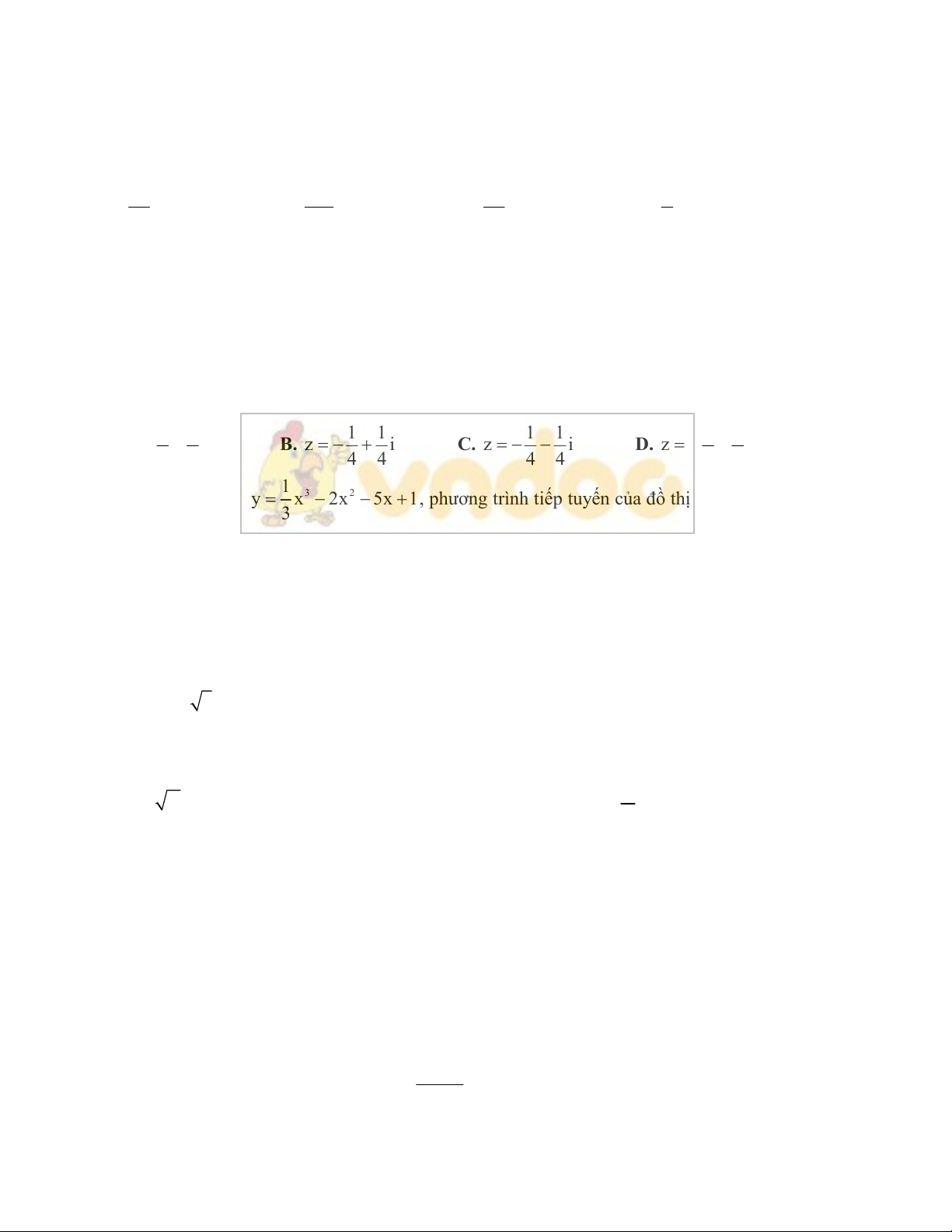
Câu 1: Cho (H) là hình phẳng giới hạn bởi parabol
2
x
y9
và đường thẳng 2x 3y 0 . Tính thể
tích khối tròn xoay khi quay hình phẳng (H) (Phần tô đậm) quanh trục hoành.
A. 4B. 96
5
C. 64
5
D. 625
81
Câu 2: Cho hàm số

yfx có bảng biến thiên như sau
Hàm số

yfx đồng biến trên khoảng nào dưới đây?
A.

0;2 B. (;2) C.

2;0D.

0;
Câu 3: Hiện nay (năm 2018) Huyện Cam Lâm có tổng dân số là 105759 người. Biết tỉ lệ tăng dân số
bình quân hàng năm là 1,2%. Hỏi sau 5 năm, tổng dân số của Huyện Cam Lâm sẽ đạt bao nhiêu người
(kết quả làm tròn đến hàng trăm)?
A. 112000 B. 112300 C. 112260 D. 112259
Câu 4: Cho hình chóp .S ABC có đáy
A
BC là tam giác vuông tại
A
, 2
B
Ca,
0
30ACB ; biết
3SA SB SC a
. Tính thể tích hình chóp.
A. 3
26aB. 36aC.
36
2
a
D.
36
3
a
Câu 5: Tổng giá trị tất cả các nghiệm nguyên dương của bất phương trình
 
31
3
log2lo 2 3g4x 23x bằng
A. 6B. 4C. 5D. 3
Câu 6: Trong không gian Oxyz viết phương trình mặt phẳng (P) chứa trục Oy và đi qua điểm
(1; 2; 3)M.
A. 360
x
z B. 30
x
z C. 310
x
z D. 3100
x
z
Câu 7: Tập xác định của hàm số 23
yx

là
A. RB. (0; ) C.
R\ 0 D. [0; )
x –-2 0 2 +∞
y' –0 + 0 –0 +
y
+∞
2
6
2
+∞
THPT TRẦN BÌNH TRỌNG
----------------
Trang 2/6 - Mã đề thi 132
Câu 8: Cho hàm số 42 2
ymx (m 9)x 8. Với giá trị nào của tham số m hàm số đã cho có ba cực
trị?
A. m3 B. 0m3
C. m3
0m3


D. m3
Câu 9: Tính diện tích hình phẳng (H) giới hạn bởi các đường 2
yx 4x và y x
A. 25
3 B. 125
6 C. 25
2 D. 9
2
Câu 10: Trong một bài thi trắc nghiệm khách quan gồm 50 câu. Mỗi câu có 4 phương án trả lời, trong
đó chỉ có một phương án đúng. Một học sinh chuẩn bị bài không tốt nên làm bài bằng cách với mỗi câu
đều chọn ngẫu nhiên một phương án trả lời. Tính xác suất để học sinh đó trả lời không đúng cả 50 câu.
A. 50
(0,25) B. 50
(0,75) C. 50
(0,8) D. 50
(0,2)
Câu 11: Hàm số nào dưới đây thỏa mãn hệ thức 2
y2y 20
?
A. ysin2x B. ytan2x C. ycos2x D. ycot2x
Câu 12: Số phức nào dưới đây thỏa mãn phương trình

1 2i z 3z 2i
A. 11
zi
22
 B. 11
zi
44
 C. 11
zi
44
 D. 11
zi
22
Câu 13: Cho hàm số 32
1
yx2x5x1
3
, phương trình tiếp tuyến của đồ thị hàm số tại điểm có tọa
độ (0;1) là
A. y5x1 B. y5x1 C. y5x1 D. y5x1
Câu 14: Trong không gian Oxyz viết phương trình tham số đường thẳng (d) đi qua điểm (3;4;1)A và
song song với trục Oz
A.
3
4
13
x
y
zt


B.
3
4
t
yt
zt

C.
3
4
1
x
t
y
z

D.
3
4
1
x
yt
z


Câu 15: Với ,
là hai số thực dương bất kì, mệnh đề nào dưới đây sai?
A. log log log

B. log log log( )

C. 100
log log D. log log log

Câu 16: Họ nguyên hàm của hàm số

fx 2x sinx là
A. xCcos x B. 2
xco Csx
C. xCcos x
D. 2
xco Csx
Câu 17: Cho
7
1
f(x)dx 10
, tích phân
4
1
f(2x 1)dx
bằng
A. 7 B. 14 C. 5 D. 17
Câu 18: Cho hàm số x
f(x) 5. Biểu thức

fx 3 25 fx 2 được rút gọn là
A. f(x) B. 126f (x) C. 25f (x) D. 5f (x)
Câu 19: Số tiệm cận của đồ thị hàm số 2
2x
y4x
bằng
A. 3 B. 1 C. 4 D. 2
Trang 3/6 - Mã đề thi 132
Câu 20: Biết


1
2
0
ln x 1 x dx ln a b 2 c
với a,b,c là các số thực dương. Tính Tabc
A. T3 2 B. T3 2 C. T1 2 D. T1 2
Câu 21: Cho hình nón, biết độ dài đường sinh bằng l, bán kính đường tròn đáy bằng r. Tính diện tích
xung quanh của hình nón.
A.
2
1
3rl
B.
1
2rl
C. 2rl
D. rl
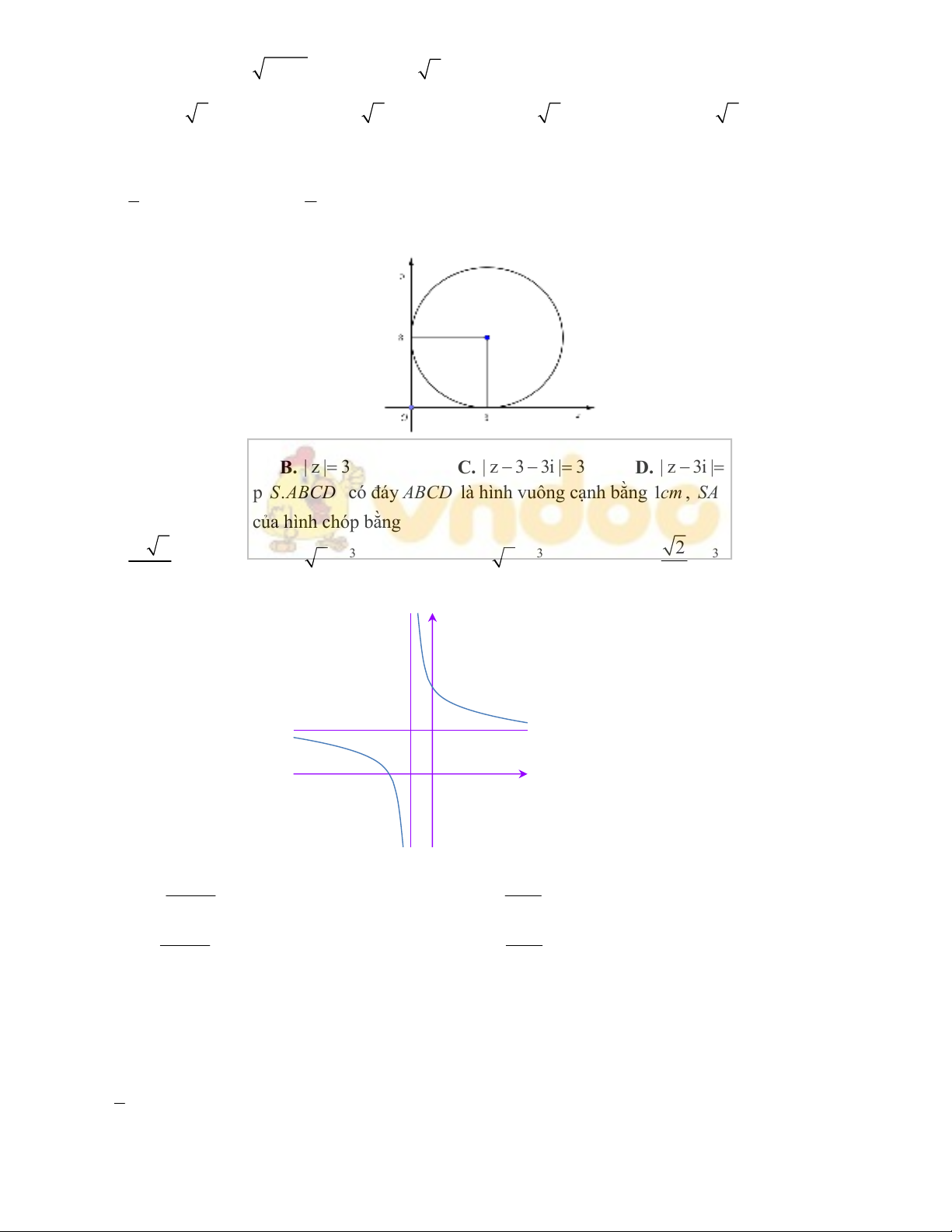
Câu 22: Đường tròn bên dưới là tập hợp điểm biểu diễn cho số phức z thỏa mãn đẳng thức
A. |z 3| 3
B. |z| 3 C. |z 3 3i| 3 D. |z 3i| 3
Câu 23: Cho hình chóp .SABCD
có đáy
A
BCD là hình vuông cạnh bằng 1cm , ()SA ABCD và
SA AC. Thể tích của hình chóp bằng
A.
3
3
a2
cm
3 B. 3
2cm C. 3
32cm D.
3
2
3cm
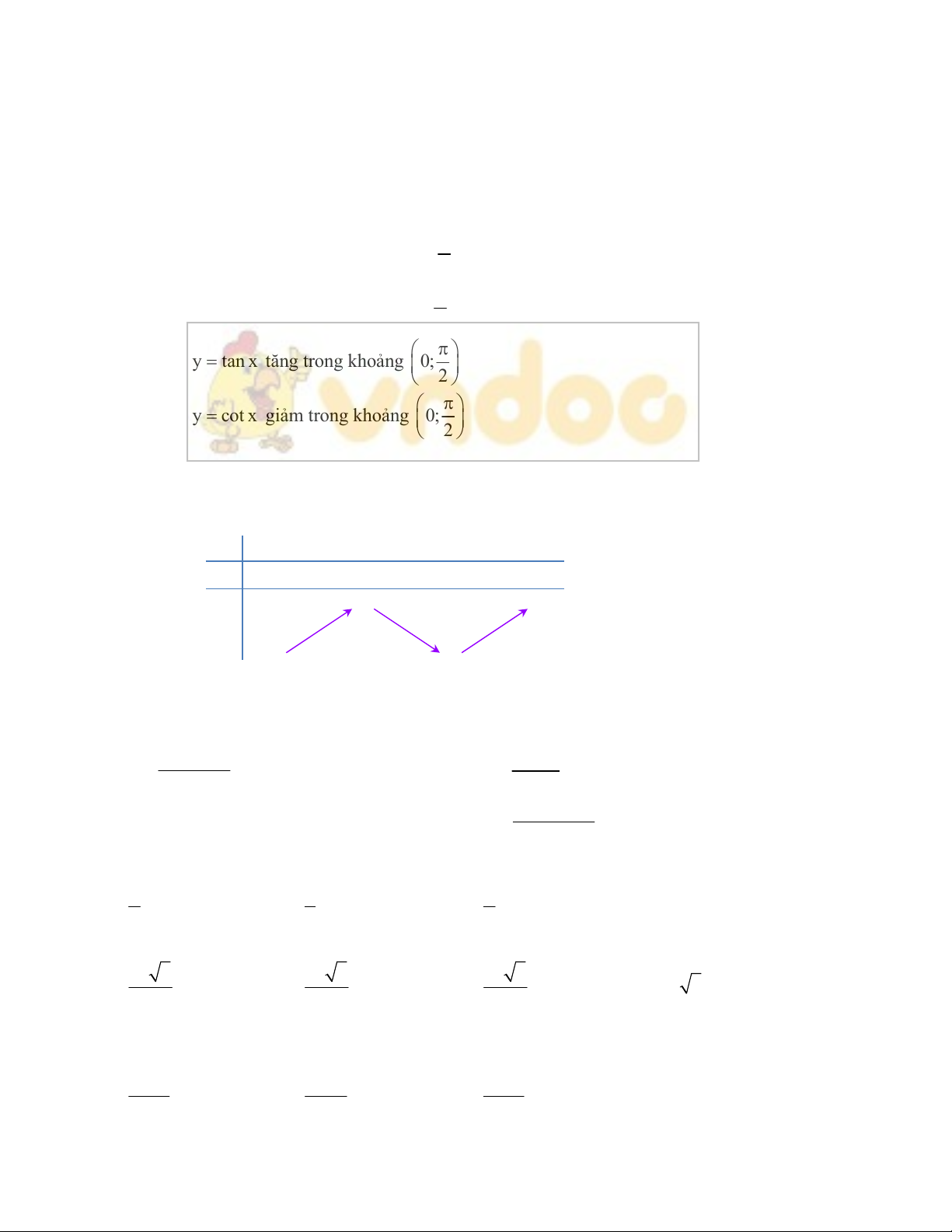
Câu 24: Đường cong trong hình bên dưới là đồ thị của hàm số nào dưới đây?
A. 2x 4
yx1
B.
2x
yx1
C. 2x 4
yx1
D. 2
yx1
Câu 25: Trên tập hợp các số phức, gọi 123
z,z,z là ba nghiệm của phương trình
32
z8z37z500 . Tính giá trị biểu thức 123
P|z| |z| |z|
A. P10 B. P9 C. P11 D. P12
Câu 26: Có bao nhiêu giá trị nguyên dương của tham số k để hàm số

32 2
1
yxk1xk3x8k
3
 đồng biến trên khoảng

0;3 ?
A. 1 B. 2 C. 3 D. 0 không
y
x
O
Trang 4/6 - Mã đề thi 132
Câu 27: Cho hai hàm số f(x), g(x) liên tục trên đoạn [a;b] và số thực k tùy ý. Trong các khẳng định
sau, khẳng định nào sai?
A.
bb
aa
kf (x)dx k f (x)dx

B.
bb
aa
xf (x)dx x f (x)dx

C.

bbb
aaa
f(x) g(x) dx f(x)dx g(x)dx

D.
ba
ab
f(x)dx f(x)dx

Câu 28: Mệnh đề nào sau đây sai?
A. Hàm số ycosx tăng trong khoảng 0; 2



B. Hàm số ysinx tăng trong khoảng 0; 2



C. Hàm số ytanx tăng trong khoảng 0; 2



D. Hàm số ycotx giảm trong khoảng 0; 2



Câu 29: Tập nghiệm của phương trình 39
log 2 log 3x(x6)
là
A. {9} B. {} C. {3} D. {9, 3}
Câu 30: Cho hàm số

yfx có bảng biến thiên như sau
Hàm số

yfx đạt cực tiểu tại điểm
A. x0 B. x3 C. x1 D. x2
Câu 31: Hàm số nào dưới đây gián đoạn tại điểm x1?
A. 2
x1
yxx1

B.
2
x2
yx1
C. 2
y(x1)(x x1) D.
2
x2x1
yx1

Câu 32: Hàm số nào dưới đây là nguyên hàm của hàm số

2x 3
fx (3x 2)e
 ?
A.

2x 3
13x 1 e
2
B.

2x 3
12x 3 e
3
C.

2x 3
16x 1 e
4
D. 2x 3
(3x 1)e
Câu 33: Tính thể tích khối lăng trụ có đáy là tam giác đều cạnh a và chiều cao bằng 2a.
A.
33
4
a B.
33
2
a C.
33
6
a D. 33a
Câu 34: Cho hình thang
A
BCD vuông tại B và C, biết ,3
A
BBCa CD a
. Tính thể tích khối
tròn xoay được sinh ra khi quay hình thang quanh đường thẳng
A
B.
A.
3
5
3
a
B.
3
7
3
a
C.
3
8
3
a
D. 3
2a
x – ∞ 0 2 + ∞
y' + 0 – 0 +
y
– ∞
1
-3
+ ∞
Trang 5/6 - Mã đề thi 132
Câu 35: Giá trị nhỏ nhất của hàm số của hàm số: 42
15
yx2x
44

trên đoạn

0;3 bằng
A. 9
2 B. 7
2 C. 1 D. 11
4
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SC, N thuộc
cạnh SD sao cho SN = 3ND. Mặt phẳng (AMN) cắt hình chóp thành hai phần, gọi thể tích phần chứa
đỉnh S là v, thể tích hình chóp S.ABCD là u. Tính tỷ số v
u.
A.
27
80 B.
1
3 C.
27
53 D.
29
80
Câu 37: Trong mặt phẳng Oxy viết phương trình đường thẳng (d') là ảnh của đường thẳng (d) có
phương trình: 3240
x
y qua phép tịnh tiến theo véc tơ (2;3)u
.
A. 3240
x
y B. 3220
x
y C. 2310
x
y D. 3240
x
y
Câu 38: Tính thể tích khối trụ, biết bán kính đáy bằng a và độ dài đường sinh bằng 3a.
A. 33a
B.
33
3
a
C. 3
3a
D. 23a
Câu 39: Cho hình chóp .SABC
có đáy
A
BC là tam giác vuông tại B; ()SA ABC. Cho
,3,2AB a BC a SA a . Mặt phẳng (P) qua A và vuông góc với SC . Tính diện tích thiết diện của
hình chóp cắt bởi (P).
A.
23
3
a B.
26
4
a C.
26
3
a D.
26
5
a
Câu 40: Trong không gian Oxyz cho mặt phẳng (P): 2340
x
yz, biết (1; ; )ubc
là một véc tơ
pháp tuyến của (P). Tính 2bc.
A. 5 B. 7 C. 10 D. 9
Câu 41: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hàm số x
y3 nghịch biến trên R
B. Hàm số
x
1
y3



đồng biến trên R
C. Đồ thị hàm số x
y3 và
x
1
y3



đối xứng nhau qua trục tung
D. Đồ thị hàm số x
y3 luôn qua điểm

3;1
Câu 42: Trong không gian Oxyz cho đường thẳng 123
(): 12 1
xy z
d

. Điểm nào sau đây thuộc
()d?
A. (0;2;-4) B. (-1;2;0) C. (-2;0;-2) D. (1;6;3)
Câu 43: Biết rằng số phức z thỏa mãn (z 3 i)(z 1 3i) là số thực. Giá trị nhỏ nhất của |z| bằng
A. 2 B. 32
C. 4 D. 22
Câu 44: Cho hình hộp .'' ' '
A
BCD A B C D . Đặt ,,'AB a AD b AA c
   . Biểu thị 'AC
 theo
,,abc

.
A. 'AC abc

B. 'AC a b c

C. 'AC a b c

D. 'AC a b c
