KHOA KHOA HỌC TỰ NHIÊN ĐỀ THI THỬ THPT QUỐC GIA NĂM 2018
ĐỀ CHÍNH THỨC Môn thi: Toán
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Mã đề thi 123
Câu 1. Giá trị pq của khối đa diện lồi, đều loại
;pq không thể bằng
A. 0. B. 2. C.1. D.3.
Lời giải
Chọn D.
Có
5 loại khối đa diện lồi, đều là
3; 3 ,
3; 4 ,
4;3 ,
3; 5 ,
5;3 . Vậy ta chọn D.
Câu 2. Cho khối tứ giác đều .S ABCD có tất cả các cạnh bằng 2a. Tính theo a thể tích của khối chóp
.SABCD.
A.
3
4
3
a. B. 33a. C.
315
3
a. D.
332
3
a.
Lời giải
Chọn D.
2a
2a
O
D
A
C
B
S
Gọi O là tâm hình vuông ABCD . Khi đó SO là đường cao của hình chóp.
12
2
AO AC a
22
42 2SO a a a
2
4
ABCD
Sa
Suy ra 23
.
14
.2.4 2
33
S ABCD
Vaaa
332
3
a
.
Câu 3. Cho

dx 2
b
a
fx 
và

dx 3
b
a
gx
. Tính
 
23dx
b
a
Ifxgx


.
A. 13I . B. 13I. C. 5I . D. 5I.
Lời giải
Chọn A.
 
23dx
b
a
Ifxgx

 
2f dx 3 dx
bb
aa
xgx


2. 2 3.3 13 .
Câu 4. Cho 237
log 3 ,log 5 ,log 2abc. Tính 140
log 63 theo , ,abc.
A. 21
2
ac
a abc b

. B. 21
21
bc
c abc

. C. 21
21
ac
c abc

. D. 31
2
ab
a abc b

.
Lời giải
Chọn C.
2
222
140 (2 .5.7)
22
2log 3 log 7
log 63 log (3 .7) 2 log 5 log 7

 và 223
log 5 log 3.log 5 ab
140
1
221
log 63 121
2
aac
c
c abc
ab c



.
Câu 5. Cho bảng biến thiên của hàm số ( )
y
fx như hình vẽ bên dưới. Đồ thị hàm số đã cho có tổng số bao
nhiêu đường tiệm cận đứng và tiệm cận ngang ?
x -∞ 2 +∞
y 6 +∞
2 3
A. 1. B. 2. C. 0. D.3.
Lời giải
Chọn D.
TXĐ của hàm số là
\2D.
• Ta thấy chỉ có 1 giá trị 0
x
mà
0
()
lim
xx
y
hoặc
0
()
lim
xx
bằng  hoặc  ( (2)
lim
x
y
)
Đồ thị có 1 tiệm cận đứng là đường 2x.
• lim 6, lim 3
xx
yy
 
 Đồ thị có 2 tiệm cận ngang là đường 6y và 3y.
Vậy có tất cả 3 tiệm cận đứng và ngang.
Câu 6. Tính tổng 123 10
10 10 10 10
2 3 ... 10TC C C C .
A. 2048T. B. 5120T. C. 1024T. D. 512T.
Lời giải
Chọn B.
Ta có:

10 0 1 2 2 3 3 10 10
10 10 10 10 10
1 ...
x
CxCxCxC xC
Lấy đạo hàm 2 vế:

91223 910
10 10 10 10
10 1 2 3 ... 10
x
CxCxC xC
Cho 123 10 9
10 10 10 10
1 2 3 ... 10 10.2 5120xCCC C .
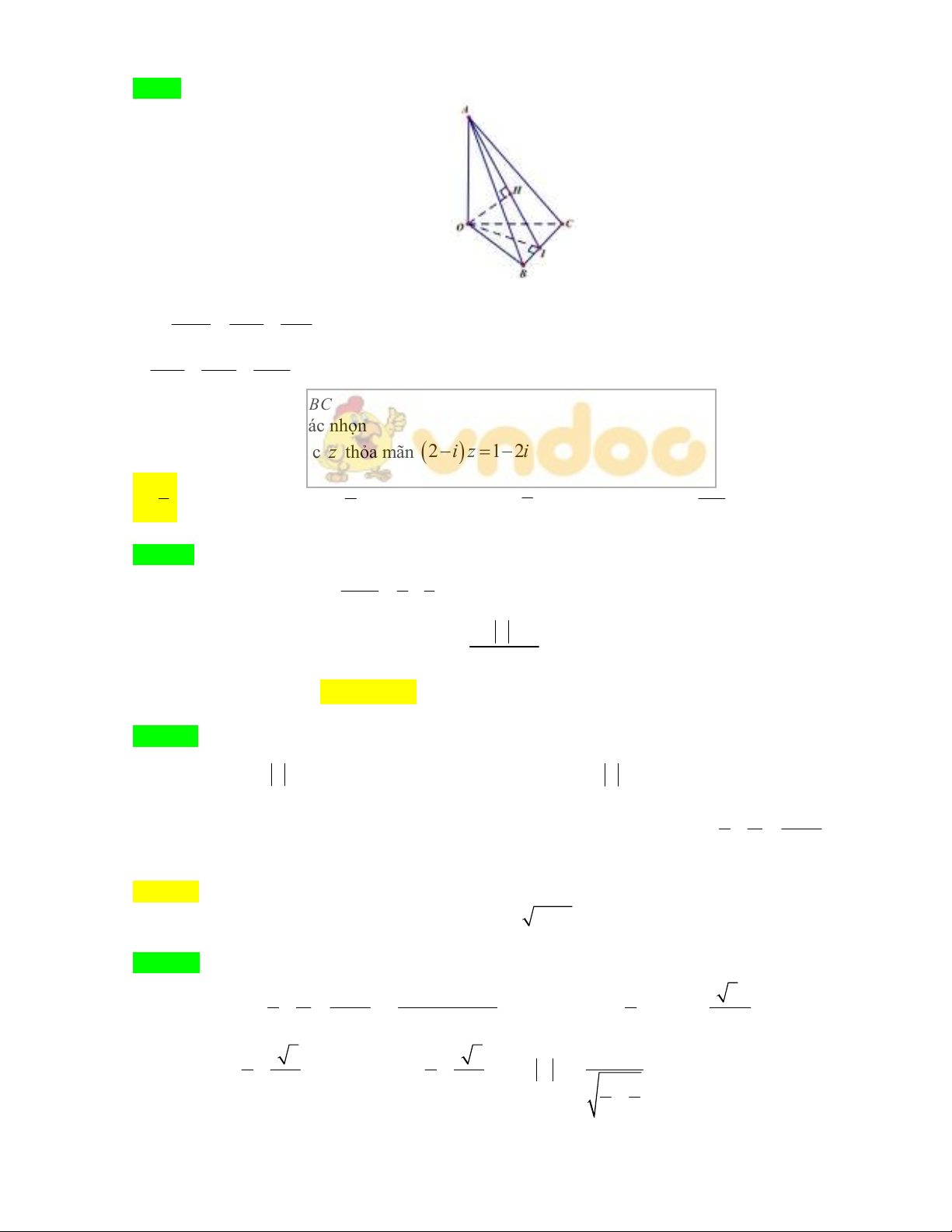
Câu 7. Cho hình chóp tam giác .O ABC có đôi một vuông góc với nhau.Gọi H là hình chiếu của O lên mặt
phẳng
A
BC .Kí hiệu 1
S, 2
S, 3
S và S
lần lượt là diện tích các tam giác
OAB , OAC , OBC và ABC . Xét các khẳng định sau:
1) 2222
1111
OH OA OB OC

3) H
là trọng tâm tam giác ABC .
2) Tam giác ABC là tam giác nhọn
4) 2 222
123
SSSS
Số khẳng định sai trong các khẳng định trên là
A. 3. B. 0. C. 1. D. 2.
Lời giải
Chọn C.
+ Ta dễ dàng chứng minh H
là trực tâm ABC
Nên 222
111
OH OA OI

(
A
HBC tại I
)
22 2
111
OA OB OC

+ Vì H
là trực tâm
A
BC
Suy ra ABC
là tam giác nhọn
Câu 8. Tìm phần ảo của số phức z thỏa mãn

212iz i
A. 3
5. B. 2
i. C. 4
5. D. 3
2
i.
Lời giải
Chọn A.
Ta có

12 4 3
212 255
i
iz i z i
i

.
Câu 9. Cho biết

1
0
d 2018fxx
. Tính tích phân
1
1
d
12018
x
f
xx
A. 2018
I
e. B. 2018I. C. 1009I. D. 2019I.
Lời giải
Chọn B.
Ta có hàm
yfx là hàm số chẵn trên

1;1, nên


11
00
d d 2018Ifxxfxx

Câu 10. Cho số phức z có môđun bằng 2018 và w là số phức thỏa mãn biểu thức 11 1
zwzw

. Môđun
của số phức w bằng
A. 2018 . B. 2019 .
C. 2017 . D. 2019 .
Lời giải
Chọn A.
Từ giả thiết ta có 11 1
zwzw



2
0
zw zw
zw z w


, suy ra
2
2
13
22
iw
zw 







Khi đó 13
22
i
zw





hoặc 13
22
i
zw





2018
13
44
w
2018.
Câu 11. Tính
2
2
1
34
lim 1
x
xx
x

:
A. 5
2
. B. 3
2
.
C. 3
2. D. 5
2.
Lời giải
Chọn B.
2
2
11
34 45
lim lim
112
xx
xx x
xx




.
Câu 12. Trong không gian với hệ tọa độ Oxyz , cho điểm

;;
M
xyz, xét các khẳng định:
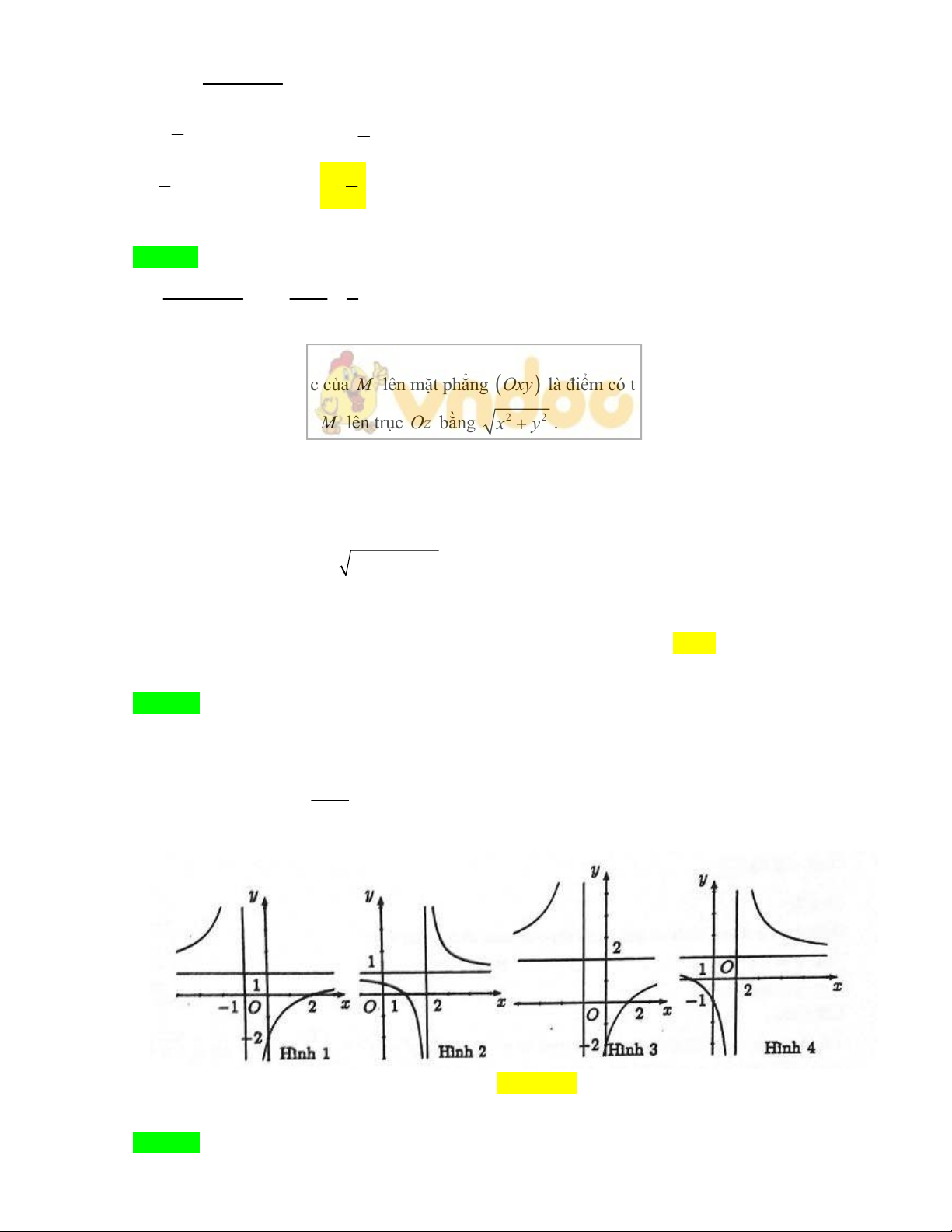
1) Hình chiếu vuông góc của
M
lên mặt phẳng

Oxy là điểm có tọa độ
;;0
x
y.
2) Khoảng cách từ điểm
M
lên trục Oz bằng 22
x
y.
3) Hình chiếu vuông góc của
M
lên trục Oy là điểm có tọa độ
0; ;0y.
4) Điểm đối xứng với điểm
M
qua trục Ox là điểm có tọa độ

;;
x
yz.
5) Điểm đối xứng với điểm
M
qua gốc tọa độ O là điểm có tọa độ
;;
x
yz.
6) Độ dài vecto OM
 bằng 222
x
yz.
Số khẳng định đúng trong các khẳng định trên là:
A. 3. B. 4. C. 1. D. 6.
Lời giải
Chọn D.
Tất cả các khẳng định trên đều đúng.
.
Câu 13. Đồ thị của hàm số 2
1
x
y
x
là một trong bốn đường cong được liệt kê trong bốn hình vẽ dưới đây.
Hỏi đồ thị đó là hình nào?
A. Hình 2. B. Hình 3. C. Hình 1. D. Hình 4.
Lời giải
Chọn C.
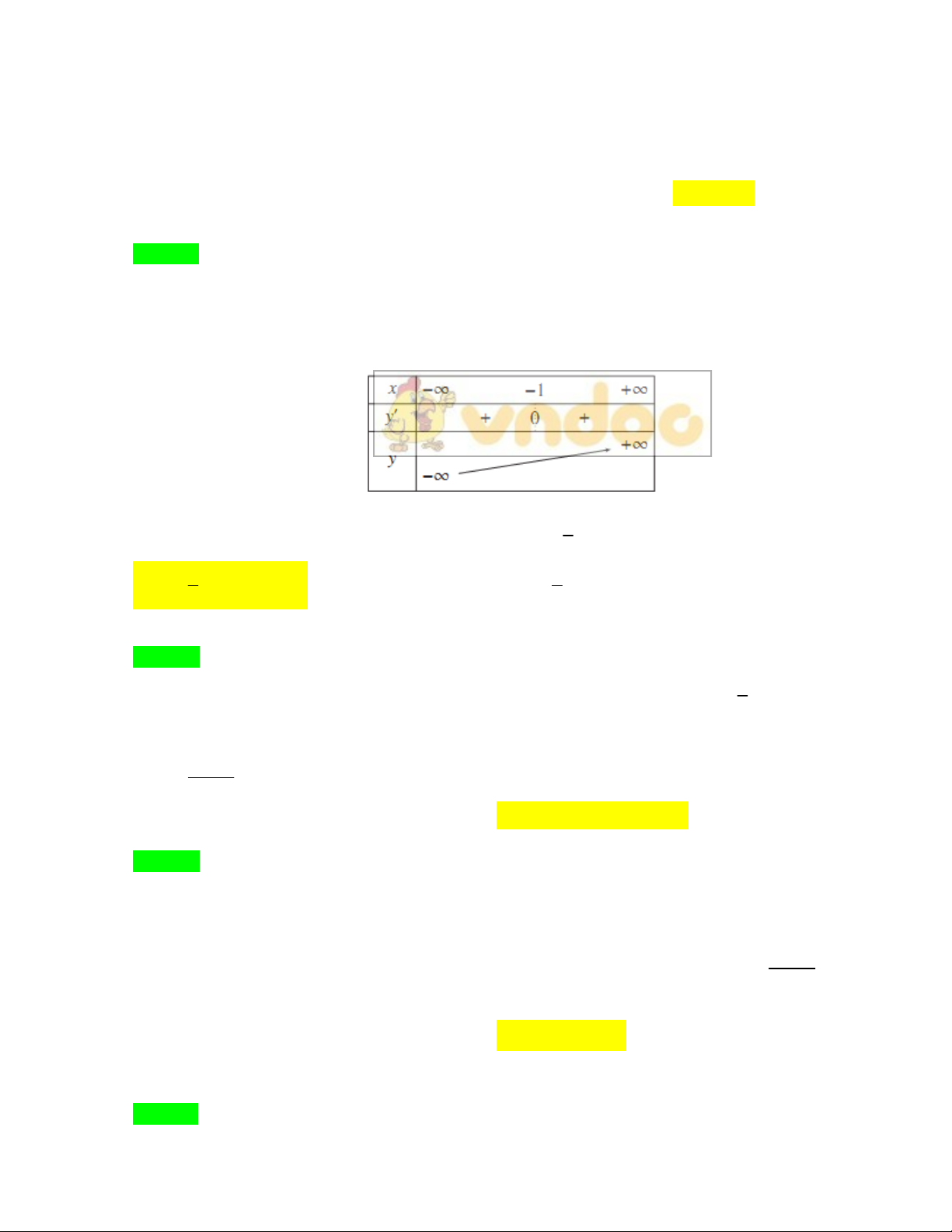
Đồ thị có đường tiệm cận đứng 1x , tiệm cận ngang 1y và đi qua các điểm
0; 2 , 2; 0 nên
chọn hình 1.
Câu 14. Phương trình tiếp tuyến của đồ thị hàm số 42
23yx x tại giao điểm của đồ thị hàm số với trục
tung là:
A. 23yx
. B. 3y. C. 23yx
. D. 3y .
Lời giải
Chọn D.
Tọa độ giai điểm của đồ thị hàm số với trục tung là

0; 3. 3
44
y
xx

,

00y. Vậy phương
trình tiếp tuyến là 3y .
Câu 15. Bảng biến thiên trong hình bên là bảng biến thiên của hàm số nào dưới đây?
A. 42
22yx x . B. 32
11
3
yxxx .
C. 32
11
3
yxxx
. D. 32
11
3
yxxx
.
Lời giải
Chọn C.
Đồ thị hàm bậc ba không có cực trị và có hệ số 0a tương ứng với hàm số 32
11
3
yxxx
Câu 16. Hàm số nào trong các hàm số sau đồng biến trên tập xác định
A. 23
15
x
y
x
. B. 42
318yx x.
C. 32
271xyx
x
. D. 32
3920xyx x.
Lời giải
Chọn D.
Xét hàm số 32
3920xyx x có tập xác định là .
29036xyx
với mọi x nên hàm số 32
3920xyx x đồng biến trên tập xác định.
Câu 17. Cho các đường cong

32
13:4Cyx x,

42
2:3Cy xx và

3
52
:1
x
Cyx
. Hỏi các
đường cong nào có tâm đối xứng?
A.

1
C,

2
C và

3
C. B.

1
C và

3
C.
C.

2
C và

3
C. D.

1
C và

2
C.
Lời giải
Chọn B.

1
C có hoành độ tâm đối xứng là nghệm của 0y và

3
Ccó tâm đối xứng là giao hai tiệm cận.