S GD&ĐT NGH ANỞ Ệ KỲ THI TUY N SINH VÀO L P 10 Ể Ớ
TR NG THPT CHUYÊN PHAN B I CHÂUƯỜ Ộ
NĂM H C 2010 - 2011Ọ
Môn thi: V T LÝẬ
Th i gian: ờ150 phút (không k th i gian giao để ờ ề)
Câu 1 (4,0 đi m)ể: Có hai bình cách nhi t đ ng cùng m t ch t l ng. M t h c sinh l n l t múc t ngệ ự ộ ấ ỏ ộ ọ ầ ượ ừ
ca ch t l ng bình 1 đ vào bình 2 và ghi l i nhi t đ khi cân b ng sau m i l n đ là: tấ ỏ ở ổ ạ ệ ộ ằ ỗ ầ ổ 1=100C,
t2=17,50C, t3 (b sót không ghi), tỏ4 = 250C. Hãy tìm nhi t đ tệ ộ 3 và nhi t đ tệ ộ 01 c a ch t l ng bình 1.ủ ấ ỏ ở
Coi nhi t đ và kh i l ng mà m i ca ch t l ng l y t bình 1 là nh nhau. B qua s trao đ i nhi tệ ộ ố ượ ỗ ấ ỏ ấ ừ ư ỏ ự ổ ệ
gi a ch t l ng v i bình, ca và môi tr ng bên ngoài.ữ ấ ỏ ớ ườ
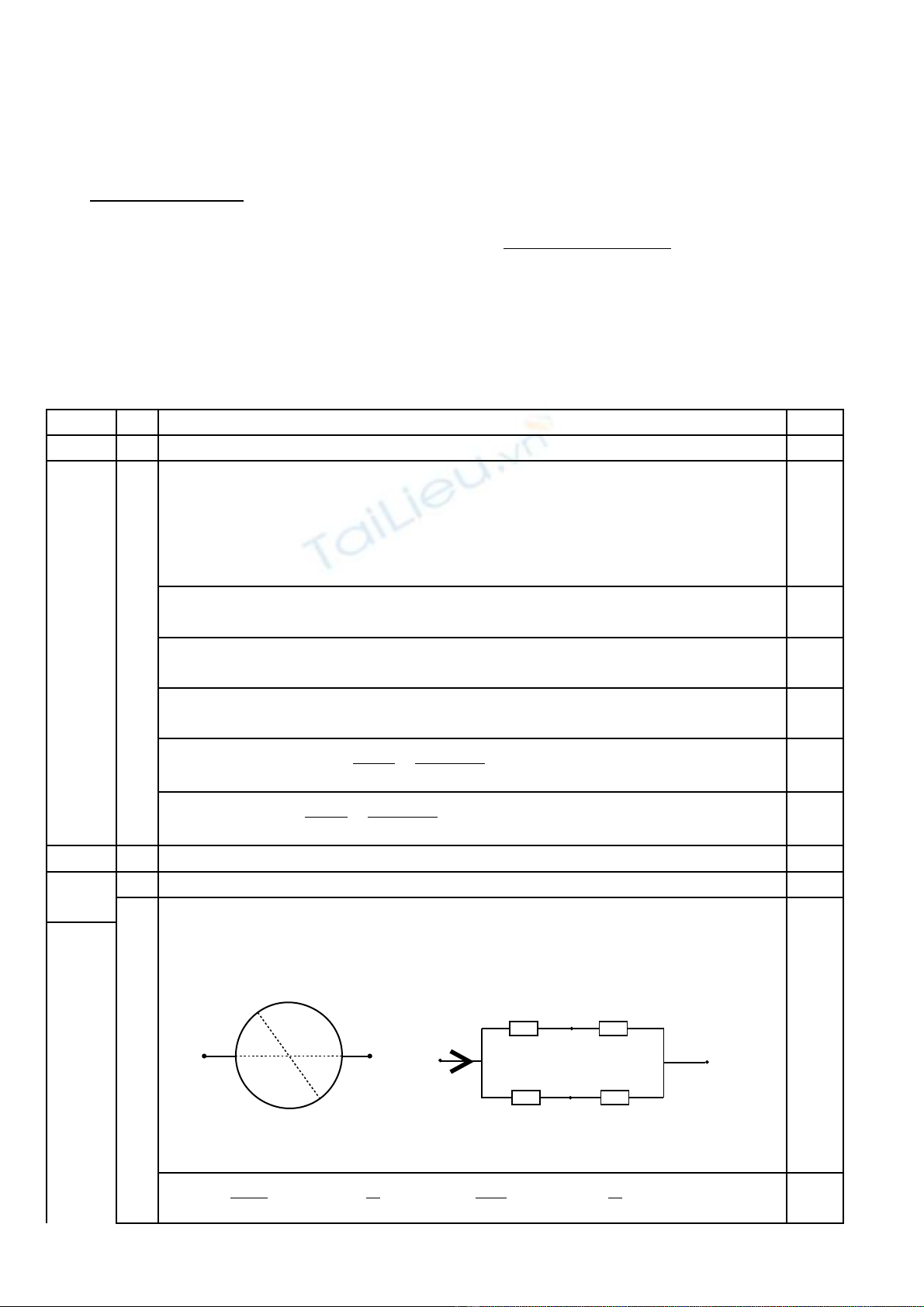
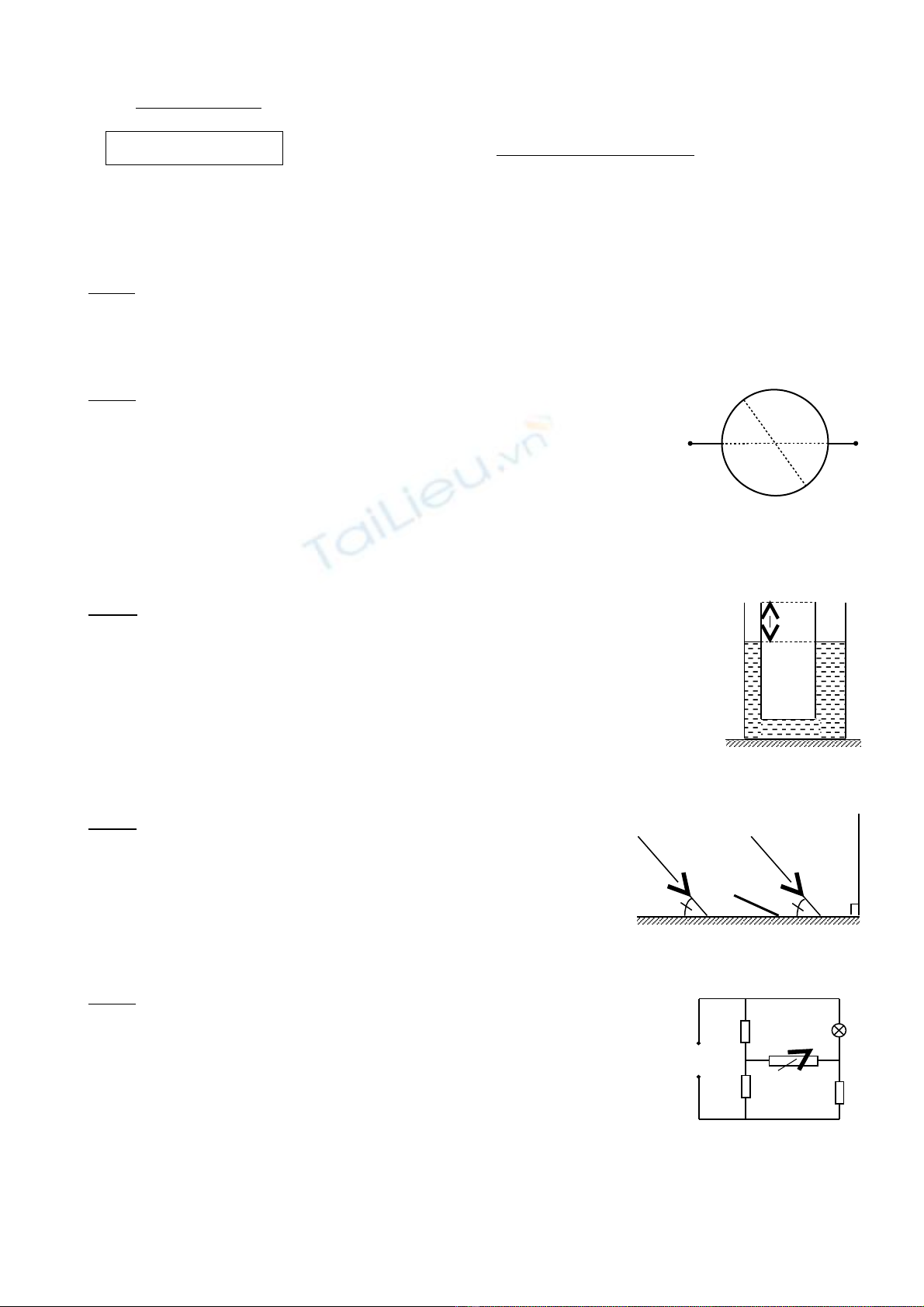
Câu 2 (4,0 đi m)ể: Hai s i dây d n đi n đ ng ch t ti t di n đ u, có cùngợ ẫ ệ ồ ấ ế ệ ề
chi u dài L, có đi n tr l n l t là Rề ệ ở ầ ượ 1 và R2 (R1 ≠ R2). Hai dây đ c u nượ ố
thành hai n a vòng tròn r i n i v i nhau t i A và B t o thành đ ng trònử ồ ố ớ ạ ạ ườ
tâm O. Đ t vào Aặ1, B1 m t hi u đi n th không đ i U, v i đ dài cácộ ệ ệ ế ổ ớ ộ
cung A1A và B1B đ u b ng x (Hình v 1). B qua đi n tr c a các dâyề ằ ẽ ỏ ệ ở ủ
n i t ngu n đ n Aố ừ ồ ế 1 và B1.
1. Tính c ng đ dòng đi n trong m ch chính theo x, L, Rườ ộ ệ ạ 1 và R2.
2. Xác đ nh x theo L, đ cho c ng đ dòng đi n m ch chính đ t:ị ể ườ ộ ệ ạ ạ
a) C c ti u.ự ể
b) C c đ i. ự ạ
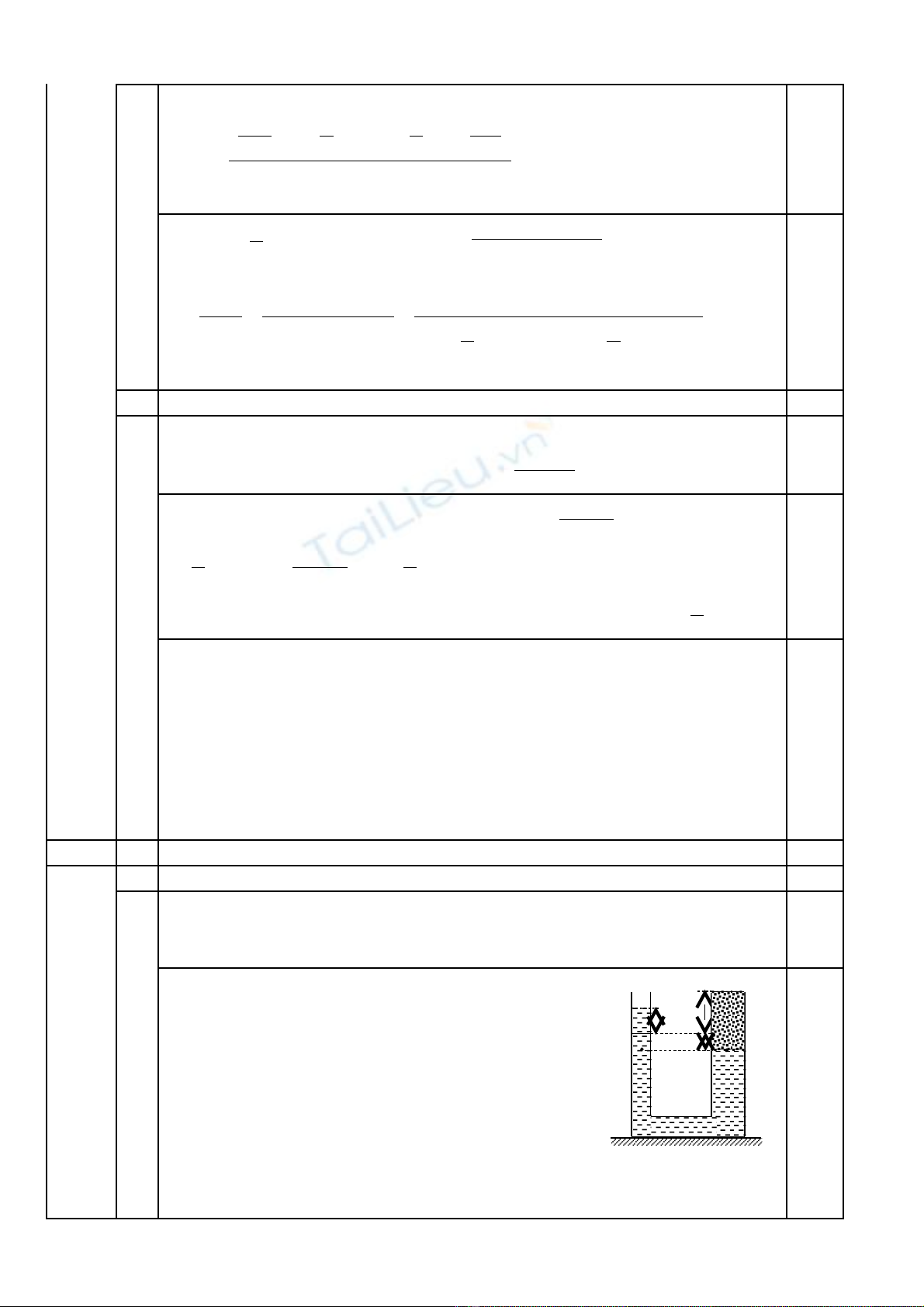
Câu 3 (4,5 đi m)ể: Cho bình thông nhau có hai nhánh A và B là hình tr , ti tụ ế
di n l n l t là Sệ ầ ượ 1 = 100cm2 và S2 = 200cm2 (Hình v 2). Hai mi ng n m trênẽ ệ ằ
cùng m t m t ph ng ngang. Lúc đ u ch a n c có đ cao đ l n, m t thoángộ ặ ẳ ầ ứ ướ ộ ủ ớ ặ
cách mi ng m i nhánh là h = 20cm, ng i ta đ t t d u vào nhánh B cho t iệ ỗ ườ ổ ừ ừ ầ ớ
lúc đ y. Cho kh i l ng riêng c a n c và d u l n l t là Dầ ố ượ ủ ướ ầ ầ ượ 1 = 1000kg/m3, D2
= 750kg/m3.
1. Tính kh i l ng d u đã đ vào nhánh B.ố ượ ầ ổ
2. Sau khi đ đ y d u vào nhánh B, ng i ta th nh nhàng m t v t hình trổ ầ ầ ườ ả ẹ ộ ậ ụ
đ c, đ ng ch t, ti t di n Sặ ồ ấ ế ệ 3 = 60cm2, cao h3 = 10cm, kh i l ng riêng Dố ượ 3 =
600kg/m3 vào nhánh A. Hãy tính kh i l ng d u tràn ra ngoài.ố ượ ầ
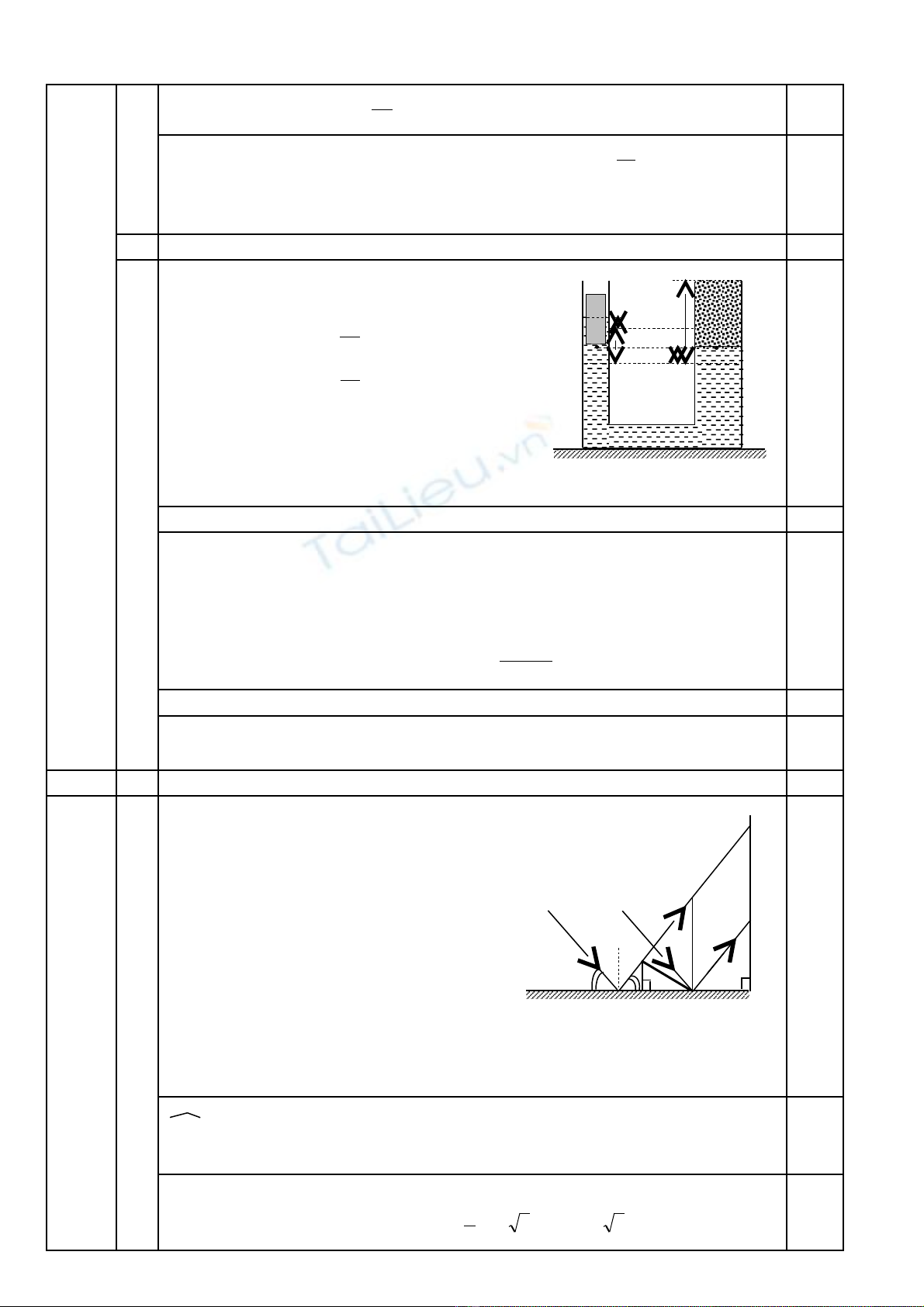
Câu 4 (3,0 đi m)ể: M t g ng ph ng G r ng đ t ng a, n m ngang,ộ ươ ẳ ộ ặ ử ằ
sát v i chân m t b c t ng cao th ng đ ng. Ng i ta đ t m tớ ộ ứ ườ ẳ ứ ườ ặ ộ
th c th ng MN có chi u dài l = 20cm nghiêng v i m t g ng m tướ ẳ ề ớ ặ ươ ộ
góc α = 300. M t chùm ánh sáng song song r ng, h p v i ph ngộ ộ ợ ớ ươ
ngang m t góc ộβ=450 chi u vào g ng. Bi t m t ph ng ch a th cế ươ ế ặ ẳ ứ ướ
và các tia sáng g p nó là m t ph ng th ng đ ng vuông góc v iặ ặ ẳ ẳ ứ ớ
t ng (Hình v 3)ườ ẽ
Xác đ nh chi u dài bóng c a th c thu đ c trên t ng.ị ề ủ ướ ượ ườ
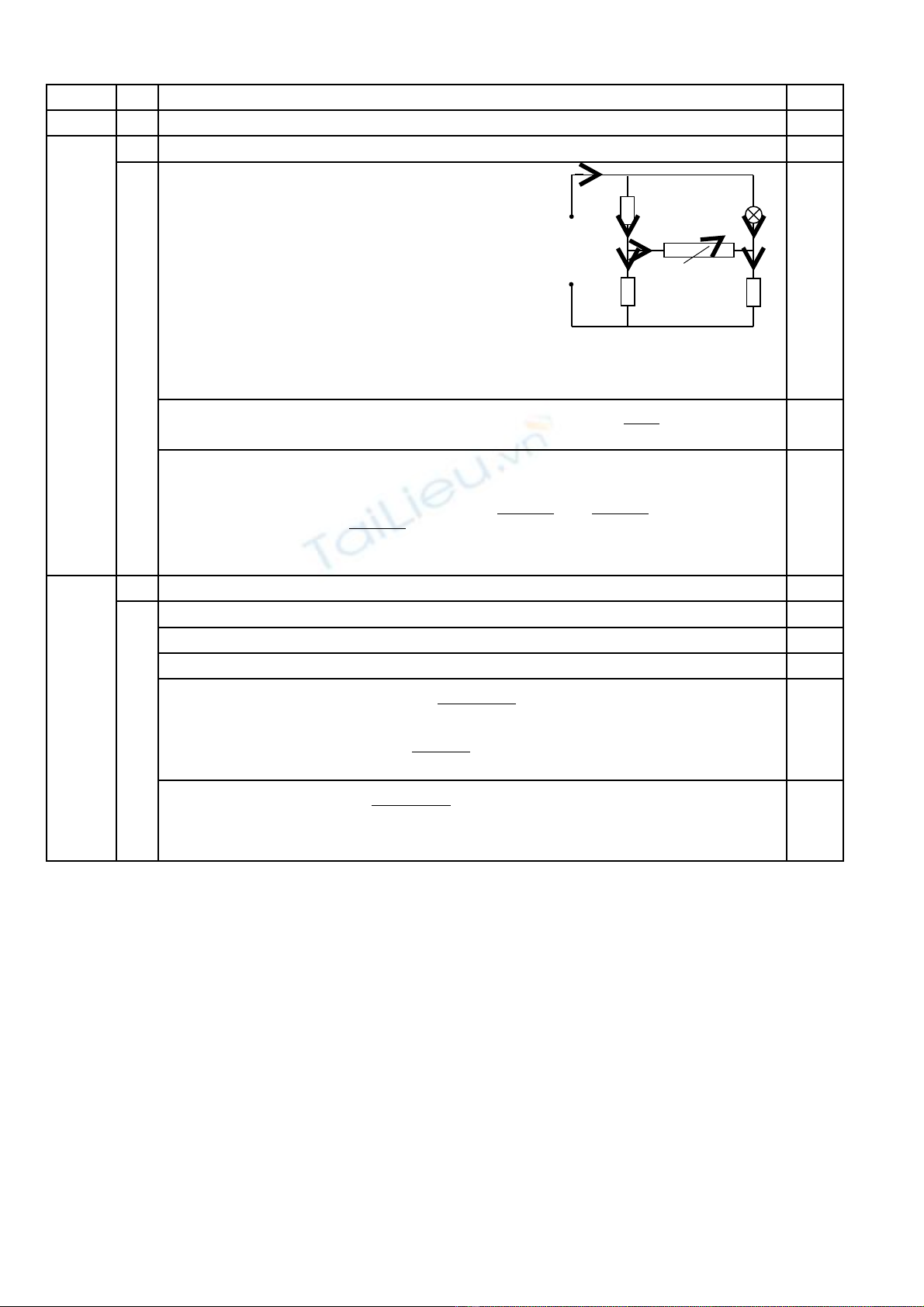
Câu 5 (4,5 đi m)ể: Cho m ch đi n nh hình v 4: Bi t Rạ ệ ư ẽ ế 1=R2=R3=R, đèn
Đ
có đi n tr Rệ ở đ = kR v i k là h ng s d ng. Rớ ằ ố ươ x là m t bi n tr , v i m iộ ế ở ớ ọ
Rx đèn luôn sáng. Ngu n đi n có hi u đi n th U không đ i đ t vào A vàồ ệ ệ ệ ế ổ ặ
B.
B qua đi n tr các dây n i.ỏ ệ ở ố
1. Đi u ch nh Rề ỉ x đ công su t tiêu th trên đèn b ng 9W. Tìm công su tể ấ ụ ằ ấ
trên R2 theo k.
2. Cho U=16V, R=8Ω, k=3, xác đ nh Rịx đ công su t trên Rể ấ x b ng 0,4W.ằ
Đ
R1
R2
Rx
A
+
U
R3
Hình 4
B
-
CD
Hình 2
A
B
h
B1
A
A1
x
Hình 1
+-
Hình 3
β
N
M
G
α
β
Đ thi chínhề
--------------------------- H tế ----------------------------
H và tên thí sinhọ:.................................................................. S báo danhố:.......................
S GD&ĐT NGH ANỞ Ệ KÌ THI TUY N SINH VÀO L P 10Ể Ớ
TR NG THPT CHUYÊN PHAN B I CHÂUƯỜ Ộ
NĂM H C 2010-2011Ọ
H NG D N VÀ BI U ĐI M CH M Đ CHÍNH TH CƯỚ Ẫ Ể Ể Ấ Ề Ứ
Môn: V T LÝẬ
(H ng d n và bi u đi m ch m g m 04 trang)ướ ẫ ể ể ấ ồ
----------------------------------
Câu ý N i dung - yêu c uộ ầ Đi mể
Câu 1 4,0
G i kh i l ng c a m i ca ch t l ng trong bình 1 là mọ ố ượ ủ ỗ ấ ỏ 0, kh iố
l ng c a ch t l ng trong bình 2 là m, nhi t dung riêng c a ch tượ ủ ấ ỏ ệ ủ ấ
l ng là Cỏ
Sau khi đ l n th nh t kh i l ng ch t l ng trong bình 2 là (mổ ầ ứ ấ ố ượ ấ ỏ
+ m0) có nhi t đ tệ ộ 1 = 100C.
0,5
Sau khi đ l n 2 ph ng trình cân b ng nhi t là:ổ ầ ươ ằ ệ
C(m + m0)(t2 - t1) = Cm0(t01 - t2) (1) 0,5
Sau khi đ l n 3 [Coi hai ca to cho (mổ ầ ả + m0) thu]
C(m + m0)(t3 - t1) = 2Cm0(t01 - t3) (2) 0,5
Sau khi đ l n 4 [Coi ba ca to cho (mổ ầ ả + m0) thu]
C(m + m0)(t4 - t1) = 3Cm0(t01 - t4) (3) 0,5
T (1) và (3) ta có:ừ
Ct
tt
tt
tt
tt 0
01
401
201
14
12 40
)(3 =⇒
−
−
=
−
−
(4) 1
T (1) và (2) ừ
Ct
tt
tt
tt
tt 0
3
301
201
13
12 22
)(2 =⇒
−
−
=
−
−
(5) 1
Câu 2 4,0
1 2,0
Do tính đ i x ng nên ta có th xem đi n tr dây cung ABố ứ ể ệ ở 1B là R1
và đi n tr dây cung AAệ ở 1B là R2 ta có m ch đi n t ng đ ng nhạ ệ ươ ươ ư
hình 2
0,75
1AmB
1
BxB2nBA
2
xAA R)
L
x
1(R;
L
xR
R;R)
L
x
1(R;
L
R.x
R1111 −==−==
0,25
B1
A
A1
B
x
x
Hình 1
+-
m
n
xAA
R
1
1
AmB
R
nBA
R
1
1
BxB
R
A1
B1
Hình
2
+
-
I
A
B
Khi đó đi n tr toàn m ch Aệ ở ạ 1B1 là:
21
1
21
2
BA RR
L
xR
R)
L
x
1(.R)
L
x
1(
L
xR
R11 +
+−
−+
=
0,5
Đ t ặ
)(
12
RR
L
x
X−=
ta đ c: ượ
21
21 ))((
11 RR
XRXR
RBA +
−+
=
Khi đó c ng đ dòng đi n m ch chính:ườ ộ ệ ạ
I =
−−
−+
+
=
−+
+
=
)RR(
L
x
R.)RR(
L
x
R
)RR.(U
)XR)(XR(
)RR.(U
R
U
122121
21
21
21
BA 11
0,5
2 2,0
Đ I đ t min ta ch c n xét ể ạ ỉ ầ
11 BA
R
, vì R1 + R2 không đ i, áp d ng b tổ ụ ấ
đ ng th c côsi ta có: ẳ ứ
2
21
21 )
2
RR
()XR)(XR( +
≤−+
0,5
Nên
11 BA
R
c c đ i khi Rự ạ 1 + X= R2 - X
2
21 RR
X−
=→
22
)( 21
12
L
x
RR
RR
L
x=→
−
=−→
V y c ng đ dòng đi n m ch chính đ t c c ti u khi x =ậ ườ ộ ệ ạ ạ ự ể
2
L
0,5
Đ I đ t max ta thì ph i có (Rể ạ ả 1+ X)(R2-X) đ t min khi 0 ≤ x ≤ Lạ
Ta th y f(X) = (Rấ1+ X)(R2-X) = -X2 + (R2 - R1)X + R1.R2
Vì f(X) là hàm s b c 2 có h s A = -1< 0 nên đ th là m t ph nố ậ ệ ố ồ ị ộ ầ
parabol quay b l m xu ng d i.ề ỏ ố ướ
Xét hai c n x = 0 và x = L thì t ng ng X = 0 và X = Rở ậ ươ ứ 2 - R1 khi
đó f(X) đ u b ng nhau, đ t c c ti u và b ng f(X) min = Rề ằ ạ ự ể ằ 1R2
V y I max khi x =0 ho c khi x = L nghĩa là khi Aậ ặ 1 trùng A; B1 trùng
B ho c Aặ1 trùng B; B1 trùng A
0,5
0,5
Câu 3 4,5
1 2,5
G i x đ dâng m c n c nhánh A, y là đ h xu ng c a m cọ ộ ự ướ ở ộ ạ ố ủ ự
n c nhánh B khi d u đ y.ướ ở ầ ầ
Ta có:
21 SyxS =
⇒
x=2y (1) 0,5
G i M, N là hai đi m cùng n m ngang v i m t ph ngọ ể ằ ớ ặ ẳ
phân cách gi a d u và n c A và B (hình v 3)ữ ầ ướ ẽ
Ta có: PM = PN => (x+y)d1 = (h+y)d2
⇒
x+y = (h+y).0,75 (2)
0,5
0,5
Hình
3
A
B
h
xy
MN
T (1) và (2) ta có: ừ
cmy 3
20
=
.0,5
Th tích d u đã đ vào nhánh B là: V = Sể ầ ổ 2(h+y) =
33
10.
3
16 m
−
Kh i l ng d u đã đ vào nhánh B là: m = V.Dố ượ ầ ổ 2 = 4kg 0,5
2 2,0
Khi kh i tr cân b ng n c dâng lên ố ụ ằ ướ ở
các nhánh A, B l n l t là a, bầ ượ
V i: ớ
=+≤≤
=−≤≤
cm
3
80
yhb0
cm
3
20
xha0
G i th tích chi m ch c a kh i trọ ể ế ổ ủ ố ụ
trong n c là Vướ 1. Do D3 < D1 nên kh i trố ụ
n i trên n c. Fổ ướ A=P3. T c là: Vứ1d1=V3d3
=> V1=360cm3
0,5
M t khác Vặ1 = a.S1 + bS2 => a + 2b = 3,6 (3) 0,25
G i C, D là hai đi m cùng n m ngang v i m t ph ng phân cáchọ ể ằ ớ ặ ẳ
gi a d u và n c A và B sau khi th kh i tr (hình v 4)ữ ầ ướ ả ố ụ ẽ
PC = PD => ( x + y – b + a)d1 = (h+y-b)d2
(x+y)d1 + (a-b)d1 = (h+y)d2 - b.d2.
Theo câu 1: (x+y)d1 = (h+y)d2 =>
ab
d
dd
ba 4
2
21 =⇒
−
=
(4) 0,5
T (3) và (4) a = 0,4cm, b = 1,6cm th a mãn v i đi u ki n trên.ừ ỏ ớ ề ệ 0,25
V y th tích đã tràn ra kh i bình B là: ậ ể ỏ ∆V = b.S2 = 0,32.10-3m3
Kh i l ng d u tràn ra ngoài là: ố ượ ầ ∆m = ∆V.D2 = 0,24kg 0,5
Câu 4 3,0
Ph n chùm tia sáng ph n x tầ ả ạ ừ
g ng không b MN ch n h t lênươ ị ắ ắ
t ng t o ra vùng sáng trên t ng,ườ ạ ườ
còn ph n b MN ch n s t o bóng c aầ ị ắ ẽ ạ ủ
MN trên t ng. Ph n chùm sáng t iườ ầ ớ
chi u tr c ti p lên th c không ph nế ự ế ướ ả
x trên g ng. Do đó bóng c a th cạ ươ ủ ướ
trên t ng là đo n AB nh hình 5.ườ ạ ư
Phâ
n
tích
cho
0,5đ
Hìn
h
vẽ
cho
1,5đ
T hình v ta th y AB = NK mà theo đ nh lu t ph n x ánh sánh taừ ẽ ấ ị ậ ả ạ
có:
MIN = β = 450 suy ra AB = NK= IN.tanβ = IN
0,5
IN = IH + HN = MH.tanβ + MN.cosα
= MN.sinα.tanβ + MN.cosα =
cm3,27)31(10)31(
2≈+=+
0,5
A
B
β
N
M
G
α
Hình
K
I
H
Hình
A
B
h+y
V1
b
CD
a
V1
x+y
V y chi u dài bóng c a th c trên t ng là: AB = 27,3cmậ ề ủ ướ ườ
Câu 5 4,5
1 2,0
Gi s chi u dòng đi n qua Rả ử ề ệ x có chi uề
nh hình v 6.ư ẽ
T s đ m ch đi n ta có:ừ ơ ồ ạ ệ
+=
+=
+=+
xd
x
III
III
UUUU
3
21
3d21
(1) 0,75
IđRđ+(Iđ+Ix)R=(I2+Ix)R+I2R=> (k+1)Iđ=2I2 =>
2
1k
I2
+
=
Iđ (2) 0,75
K t h p (1) và (2) ta có:ế ợ
W)(9.
k4
)1k(
P
k4
)1k(
P
RI
4
)1k(
P
RkIP
RIP
kRIP 2
d
2
2
2
d
2
2
2
dd
2
22
2
dd +
=
+
=⇒
+
=
=
⇒
=
=
0,5
2 2,5
Khi k=3 theo ý 1=> I2=2Id (3) không ph thu c Rụ ộ x0,5
Theo s đ m ch đi n hình 6 ta có: Uơ ồ ạ ệ đ+U3=U => 4Iđ=2-Ix (4) 0,5
U2=Ux+U3 => I2R=IxRx+(Iđ +Ix)R (5) 0,5
t (3), (5) thay s ta có: Iừ ố đ=
8
)8R(I xx +
(6)
T (4) và (6) suy ra: Iừx=
10R
4
x+
(7) 0,5
Ta l i có: Pạx=Ix2Rx=
0100R20R4,0
)10R(
R16
x
2
x
2
x
x=+−⇒=
+
=> Rx=10Ω0,5
Ghi chú: + T t c các bài toán n u gi i theo cách khác mà đúng đ u cho đi m t i đa.ấ ả ế ả ề ể ố
+ M t l n thi u đ n v tr 0,25đ, còn 2 l n tr lên trong c bài thi tr t i đaộ ầ ế ơ ị ừ ầ ở ả ừ ố
0,5đ.
R1
R2
R3
Đ
Rx
A
+
B
-
C D
UI1
I2
Ix
Iđ
I3
I
Hình