
1
Chương 3 Mô hình không gian tín hiệu
3.1 Mô hình hệ truyền tin số băng thông dải
3.2 Qui trình trực giao hóa Gram-Schmidt
3.3 Ý nghĩa hình học của biểu diễn tín hiệu
3.4 Đáp ứng của dãy các bộ tương quan lối vào
3.5 Tách tín hiệu đồng bộ trong ồn
3.6 Bộ thu tương quan
3.7 Xác suất lỗi
3.8 Tách tín hiệu không biết pha trong ồn
Trong truyền tin số băng cơ sở, dữ liệu chuyển thành các tín hiệu PAM rời rạc truyền
trực tiếp trên kênh thông thấp. Vấn đề chính là tạo dạng xung (do phối hợp cả bộ lọc nơi
phát và nơi thu) để kiểm soát ISI.
Khi xét đến truyền tin số băng thông dải, dòng dữ liệu sẽ được điều chế lên sóng
mang (giá trị tần số sóng mang này tùy theo tính chất kênh). Vấn đề chính ở đây là thiết
kế tối ưu bộ thu để tối thiểu xác suất lỗi ký hiệu khi có ồn. Điều này không có nghĩa là
ồn không ảnh hưởng đến truyền xung băng cơ sở, cũng như không có nghĩa ISI không
ảnh hưởng đến truyền tin số băng thông dải. Đây chỉ là 2 vấn đề nổi bật trong 2 phạm vi
truyền dẫn.
PSK (khóa dịch pha) và FSK (khóa dịch tần) không sợ tính phi tuyến về biên độ của
kênh truyền nên trong truyền tin số băng thông dải chúng hay được sử dụng hơn
ASK(khóa dịch bên độ), thể hiện đặc biệt trong thông tin vệ tinh, hay vi ba. Các vấn đề sẽ
được phân tích kỹ ở đây là: Thiết kế tối ưu bộ thu để có ít lỗi, tính xác suất lỗi ký hiệu
trung bình trong kênh có ồn và xác định tính chất phổ của tín hiệu điều chế. Hai trường
hợp điển hình được xem xét là kỹ thuật đồng bộ (bộ thu bám pha với ký hiệu đến) và kỹ
thuật không đồng bộ (tức là không có đồng bộ pha giữa bộ thu và ký huệy đến). Để chuẩn
bị cho việc phân tích và đánh giá các kỹ thuật nói trên ta nêu ra trước hết lý thuyết tổng
quát về không gian tín hiệu.
3.1 Mô hình hệ truyền tin số băng thông dải
Giả sử mi là một ký hiệu thuộc tập M ký hiệu của bản tin. mi sẽ được truyền trong
thời gian T và có xác suất xuất hiện giả sử là pi=P(mi)=1/M (xác suất trước hay còn gọi
là xác suất tiền nghiệm).
Để tạo ra tín hiệu truyền, mi được đưa vào bộ tạo véc tơ (mã hóa ký hiệu truyền) ứng
với véc to N chiều: si=(si1,si2,…siN) với N≤M. Tức là tín hiệu truyền được coi là một véc
to trong không gian có hệ cơ sở N chiều
Các thành phần của vecto được đưa vào bộ điều chế tạo nên tín hiệu si(t) (i=1,2,..M)
có độ dài T giây. Tín hiệu này có năng lượng hữu hạn:
∫
=
T
ii dttsE
0
2)( i=1,2..,M (3.1)
Và si(t) còn gọi là điểm tín hiệu trong không gian M tín hiệu
Kênh truyền giả sử có 2 tính chất:
1) Tuyến tính, độ rông băng đủ lớn để không làm méo si(t).
2
2) Kênh có ồn Gauss cộng tính trung bình zero và dừng (AWGN) (Giả thiết này ứng
với kênh điển hình trên thực tế)
Tín hiệu sau khi qua kênh sẽ là
x(t)=si(t)+w(t) 0≤t≤T
Bộ thu quan sát x(t) trong thời gian T giây để ước lượng tốt nhất si(t) tương ứng với mi .
Nhiệm vụ này được chia làm 2 bước.
- Bước đầu là bộ tách (còn gọi là giải điều chế): tách được các thành phần của véc tơ
x(t). Do quá trình ngẫu nhiên của ồn nên x(t) cũng là véc to của biến ngẫu nhiên X.
- Bước 2 gọi là giải mã tín hiệu truyền tạo nên một ước lượng m
ˆi khi quan sát vecto
nhận được x (coi rằng đã biết dạng điều chế cùng với xác suất tiền nghiệm ở bên phát
pi=P(mi))
Do ồn có tính thống kê nên việc quyết định cũng có bản chất thống kê (thỉnh thoảng
có lỗi). Yêu cầu thiết kế bộ thu phải làm sao tối thiểu xác suất trung bình của lỗi
∑
=
≠= M
i
iie mPmmPP
1
)()
ˆ
( (3.2)
Ngoài ra bộ thu nói chung còn được phân loại thành thu đồng bộ và không đồng bộ
3.2 Qui trình trực giao hóa Gram-schmidt
Nhiệm vụ chuyển bản tin mi (i=1,2,..M) thành tín hiệu được điều chế (tín hiệu mang
thông tin) si(t) gồm 2 phép toán thời gian rời rạc và phép toán thời gian liên tục.
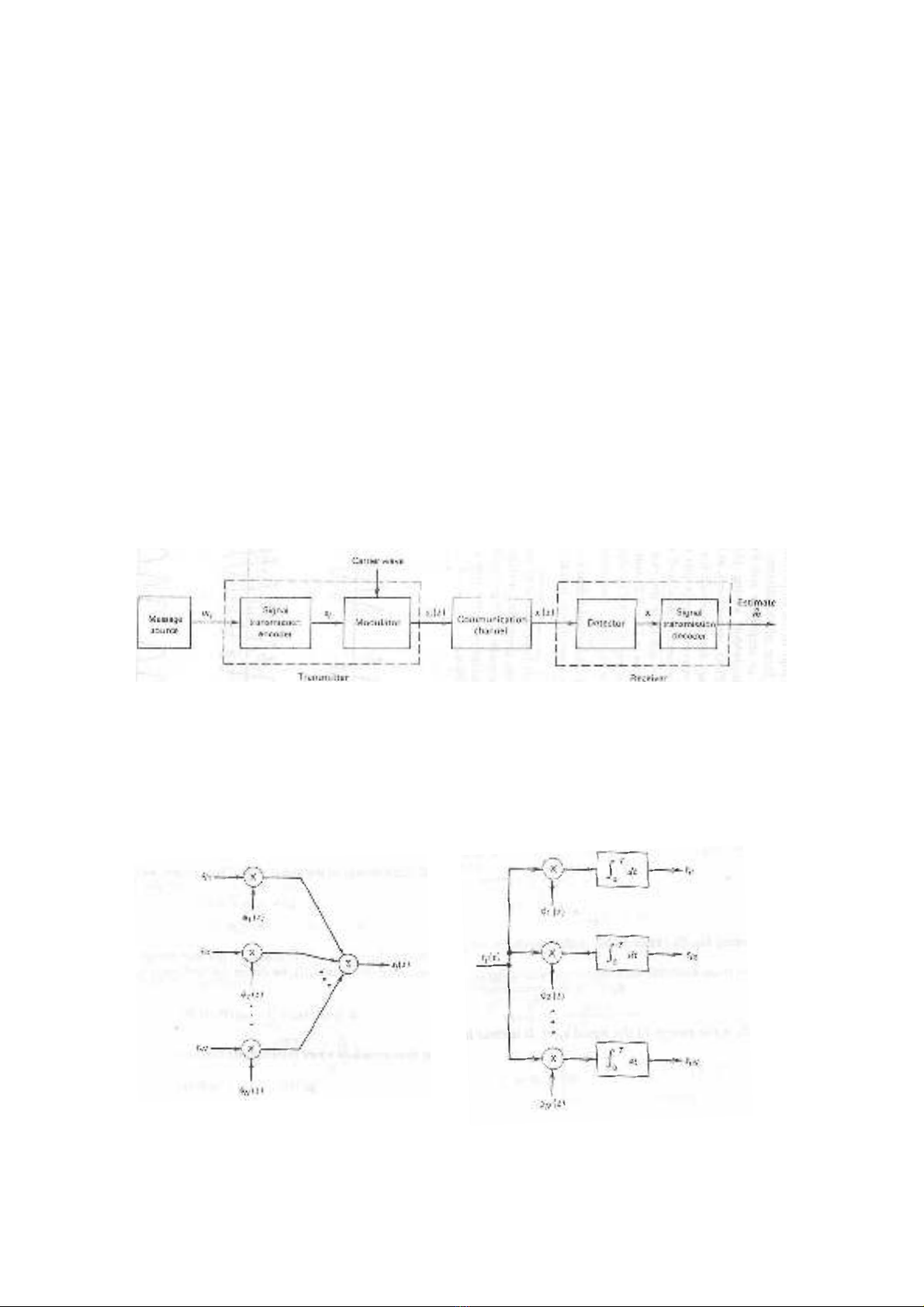
Hình 3.1 Mô hình hệ truyền tin số băng cơ sở
Hình 3.2 a) Sơ đồ phát tín hiệu si(t), b) Sơ đồ phát tập các hệ
số{si}

3
Hai phép toán này cho phép biểu diễn một tập M tín hiệu năng lượng {si(t)} như một tổ
hợp tuyến tính của N hàm trực giao có sở
∑
=
=N
j
jiji tsts
1
)()(
φ
0≤t≤T i=1,2,..M (phép toán rời rạc) (3.3)
Với ⎩
⎨
⎧
≠
=
=
∫jineu
jineu
dttt
T
ji _0
_1
)()(
0
φφ
(điều kiện chuẩn hóa và trực giao) (3.4)
Ta sẽ có ∫
=
T
jiij dtttss
0
)()(
φ
(phép toán liên tục) (3.5)
Các hệ số sij đươc coi như tọa độ của véc tơ N chiều si(t). Khi cho các tọa độ này ở lối
vào bộ tạo tín hiệu có thể tạo nên tín hiệu si(t). Sơ đồ trên hình 3.2 a có thể coi như bộ
điều chế bên phát.
Ngược lại khi cho tín hiệu si(t) (i=1,2,..M) đi vào một dãy các bộ nhân và tích phân
(còn gọi là bộ tương quan) có thể tính được các hệ số sij theo sơ đồ (hình 3.2 b). Sơ đồ
này được gọi là bộ tách hay giải điều chế bên thu
Như vậy việc điều chế và giải điều chế có thể coi như việc tổng hợp phân tích tín
hiệu thông qua các hàm cơ sở. Vấn đề là cốt lõi là xác định các hàm cơ sở từ tập M tín
hiệu định sử dụng, đây cũng chính là cơ sở cho việc thiêt kế bộ thu và phát. Quá trình tìm
các hàm cơ sở này đã được Gram-smidth nêu ra như là quá trình trực giao hóa như sau:
Trước hết ta định nghĩa hàm cơ sở thứ nhất (từ tín hiệu thứ nhất) là
1
1
1
)(
)( E
ts
t=
φ
(3.6)
Ở đó E1 là năng lượng của s1(t).
Khi đó: )()()( 111111 tstEts
φφ
== . (3.7)
Tiếp đó ta định nghĩa:
∫
=
T
dtttss
0
1221 )()(
φ
(3.8)
và đưa ra hàm trung gian )()()( 12122 tststg
φ
−
= (3.9)
hàm này trực giao với )(
1t
φ
trên khoảng 0≤t≤T. Bây giờ ta định nghĩa hàm cơ sở thứ 2:
∫
=T
dttg
tg
t
0
2
2
2
2
)(
)(
)(
φ
(3.10)
Thay vào các phương trình trên và rút gọn ta có:
2
212
1212
2
)()(
)(
sE
tsts
t−
−
=
φ
φ
(3.11)
Ở đó E2 là năng lượng của s2(t) và rõ ràng là:
1)(
0
2
2=
∫
T
dtt
φ
và 0)()(
0
21 =
∫
T
dttt
φφ
(3.12)
Tiếp tục qui trình này có thể định nghĩa:
4
∑
−
=
−= 1
1
)()()(
i
j
jijii tststg
φ
Ở đó ∫
=
T
jiij dtttss
0
)()(
φ
j=1,2,..i-1 (3.13)
Khi đó có thể định nghĩa tập hàm cơ sở:
∫
=T
i
i
i
dttg
tg
t
0
2)(
)(
)(
φ
i=1,2,..N (3.14)
Theo qui trình trực giao hóa nói trên có thể thấy
- Khi si(t) là tập M tín hiệu độc lập tuyến tính thì N=M
- Khi si(t) là tập M tín hiệu không độc lập tuyến tính thì N<M và các hàm trung
gian gi(t)=0 khi i>N
Chú ý rằng khai triển chuỗi Fourier theo các tín hiệu tuần hoàn hay biểu diễn một tín
hiệu băng giới hạn theo các mẫu của nó tại tốc độ Nyquist là những trường hợp riêng của
qui trình trên, tuy nhiên có 2 khác biệt quan trọng cần nói rõ:
- dạng các hàm cơ sở )(t
i
φ
i=1,2,..N ở qui trình trên là không xác định tức là ta
không hạn chế qui trình trực giao theo hàm sin hay hàm sinc
- Khai triển tín hiệu si(t) theo qui trình trên gồm một số hữu hạn các số hạng không
phải là một xấp xỉ mà là một biểu diễn chính xác
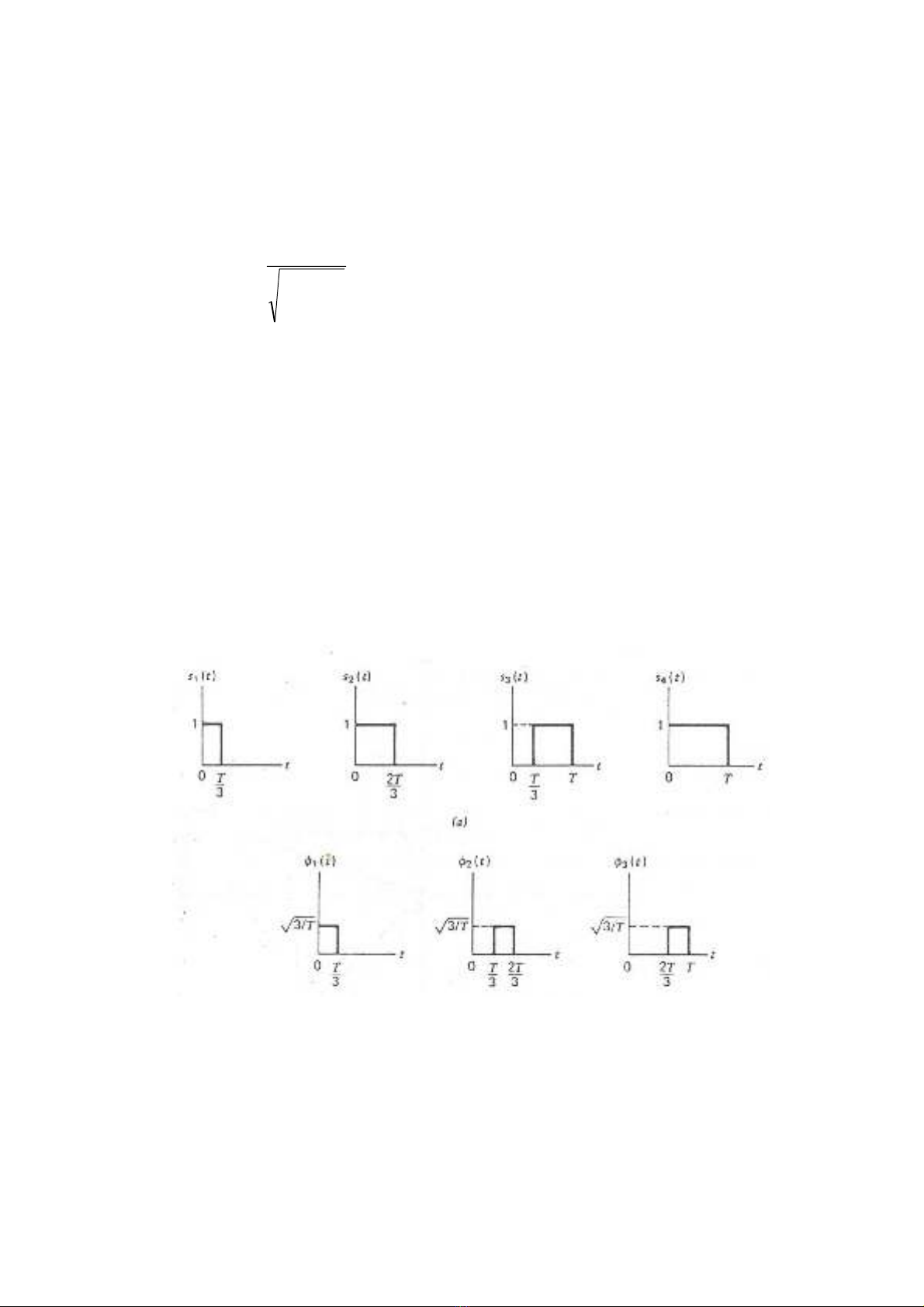
Ví dụ: Cho các tín hiệu s1(t),s2(t),s3(t),s4(t) trên hình. Dùng thủ tục Gam-Schmidt để tìm
các hàm trực giao cơ sở của các tín hiệu này
Bước 1. Năng lượng của s1(t) là:
Hình 3.3 a) Tập các tín hiệu sẽ được trực giao hóa, b) Kết quả các
hàm trực giao

5
3/)1()(
3/
0
2
0
2
11 TdtdttsE
TT
=== ∫∫ (3.15)
Hàm cơ sở đầut iên sẽ là: ⎩
⎨
⎧≤≤
== laicon
TtT
E
ts
t_0
3/0/3
)(
)(
1
1
1
φ
(3.16)
Bước 2 3
3
)1()()(
3/
00
1221
T
dt
T
dtttss
TT
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
== ∫∫
φ
(3.17)
Năng lượng của s2(t) là: 3/2)1()(
3/2
0
2
0
2
22 TdtdttsE
TT
=== ∫∫ (3.18)
Hàm cơ sở thứ 2 sẽ được tính:
⎩
⎨
⎧≤≤
=
−
−
=laicon
TtTT
sE
tsts
t_0
3/23//3
)()(
)( 2
212
1212
2
φ
φ
(3.19)
Bước 3 0)()(
0
1331 == ∫
T
dtttss
φ
(3.20)
3
3
)1()()(
3/2
3/0
2332
T
dt
T
dtttss
T
T
T
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
== ∫∫
φ
(3.21)
Vì vậy ⎩
⎨
⎧≤≤
=−−= laicon
TtTT
tstststg _0
3/2/3
)()()()( 23213133
φφ
(3.22)
Hàm cơ sở thứ 3 sẽ la: ⎩
⎨
⎧≤≤
==
∫laicon
TtTT
dttg
tg
tT_0
3/2/3
)(
)(
)(
0
2
3
3
3
φ
(3.23)
Cuối cùng với i=4 ta có g4(t) băng zero , quá trình trực giao kết thúc với M=4, N=3
3.3 Ý nghĩa hình học của tín hiệu
Mỗi tín hiệu trong tập {si(t)} được xác định như một vecto với các tọa độ của nó. Mở
rộng ra: tập M tín hiệu như tập M điểm trong khônggian Euclid N chiều với N trục vuông
góc.
Trong không gian Euclid N chiều có thể biểu diễn độ dài veto và góc giữa chúng
ji
j
T
i
ij ss
ss
=
θ
cos (3.24)
Chú ý: Năng lượng của tín hiệu bằng bình phương độ dài veto biểu diễn chúng. Thật
vậy:
∑∑
∫∑
∫===
=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
== N
j
ij
N
k
kik
TN
j
jij
T
ii sdttstsdttsE
1
2
1
01
0
2)()()(
φφ
(3.25)


























