22
fprintf(fptr,"%e",(float)0.0);
w1[0]=w2[0]=-pi;
dw=pi/16.0;
for(i=1;i<33;i++)
w1[i]=w2[i]=w1[i-1]+dw;
for(i=0;i<33;i++)
fprintf(fptr," %e",w2[i]);
xt=wherex();yt=wherey();
gotoxy(70,25);
textattr(RED+(LIGHTGRAY<<4)+BLINK);
cputs("WAIT");
gotoxy(xt,yt);
for(i=0;i<33;i++)
{
fprintf(fptr,"\n");
for(j=0;j<33;j++)
{
sum=0.0;
for(n1=-NS;n1<=NS;n1++)
for(n2=-NS;n2<=NS;n2++)
sum+=h[n1+NS][n2+NS]*(float)cos((double)(w1[i]*(float)n1+
w2[j]*(float)n2));
z[i]=sum;
}
fprintf(fptr,"%e",w1[i]);
for(j=0;j<33;j++)
fprintf(fptr,"%e",z[j]);
}
fclose(fptr);
}
xt=wherex();yt=wherey();
gotoxy(70,25);
textattr(WHITE+(BLACK<<4));
cputs(" ");
gotoxy(xt,yt);
printf("\n Press any key to exit.");
23
getch();
}
/* Dinh nghia ham cho tich phan */
float f(float x,float y)
{
float H(float,float),a;
a=H(x,y)*(float)cos((double)(x*n1))*cos((double)(y*n2));
return(a);
}
/*********************************************/
/*Chuong trinh con Simpson tinh tich phan kep*/
/*********************************************/
float simpson2( float(*f)(float,float),float xmin,float xmax, float
ymin, float ymax, int M, int N)
/* f la mot ham hai bien dinh nghia boi nguoi dung.
xmin, xmax, va ymin, ymax la gioi han cua hai tich phan.
M,N la so khoang cach tren huong x va y va chi co gia tri chan*/
{
register i,j;
float sum1,sum2,dx,dy,x,y,I;
float *A;
A=(float *) malloc(M*sizeof(float));
dx=(xmax-xmin)/(float) M;
dy=(ymax-ymin)/(float) N;
x=xmin;
for (i=0;i<=M;i++)
{
sum1=sum2=0.0;
y=ymin+dy;
for(j=1;j<N; j++)
{
if((j%2)==0)
24
sum1+=(*f)(x,y);
else
sum2+=(*f)(x,y);
y+=dy;
}
*(A+i)=(*f)(x,ymin)+2.0*sum1+4.0*sum2+(*f)(x,ymax);
x+=dx;
}
sum1=sum2=0.0;
for(i=1;i<M;i++)
{
if((i%2)==0)
sum1+=*(A+i);
else
sum2+=*(A+i);
}
I=*A+2.0*sum1+4.0*sum2+*(A+M);
return(I*dx*dy/9.0);
}
/***************************************
* Dinh nghia ham bo loc H(w1,w2). Ham *
* xac dinh boi nguoi dung *
***************************************/
float H(float w1, float w2)
{
float DO,a,R2;
DO=0.5*pi; // cut-off
R2=w1*w1+w2*w2;
a=0.414*DO*DO/(R2+0.414*DO*DO);
return(a);
}
/***************************************
Vi du ve mot so ham khac
1.Laplacian Operator.
25
a=R2;
2. Phase contrast filters
if(R2<(DO*DO))
a=1.0;
else
a=-1.0;
3. homomorphic filter
float gamah, gamal, k;
gamah=1.0;
gamal=0.5;
if (R2<(DO*DO))
{
k=(1.0)-(gamah-gamal))/(gamah-gamal);
a=(R2/(R2*DO*DO*k))+gamal;
}
else
a=gamah;
4.Low pass filter
a=0.414*DO*DO/(R2+0.414*DO*DO);
5.High pass filter
a=R2/(R2+0.414*DO*DO);
*****************************************/
Trong chương trình 2.1 đáp ứng xung được tính trên cửa sổ kích
thước 11 11 mẫu mà tâm là gốc toạ độ.
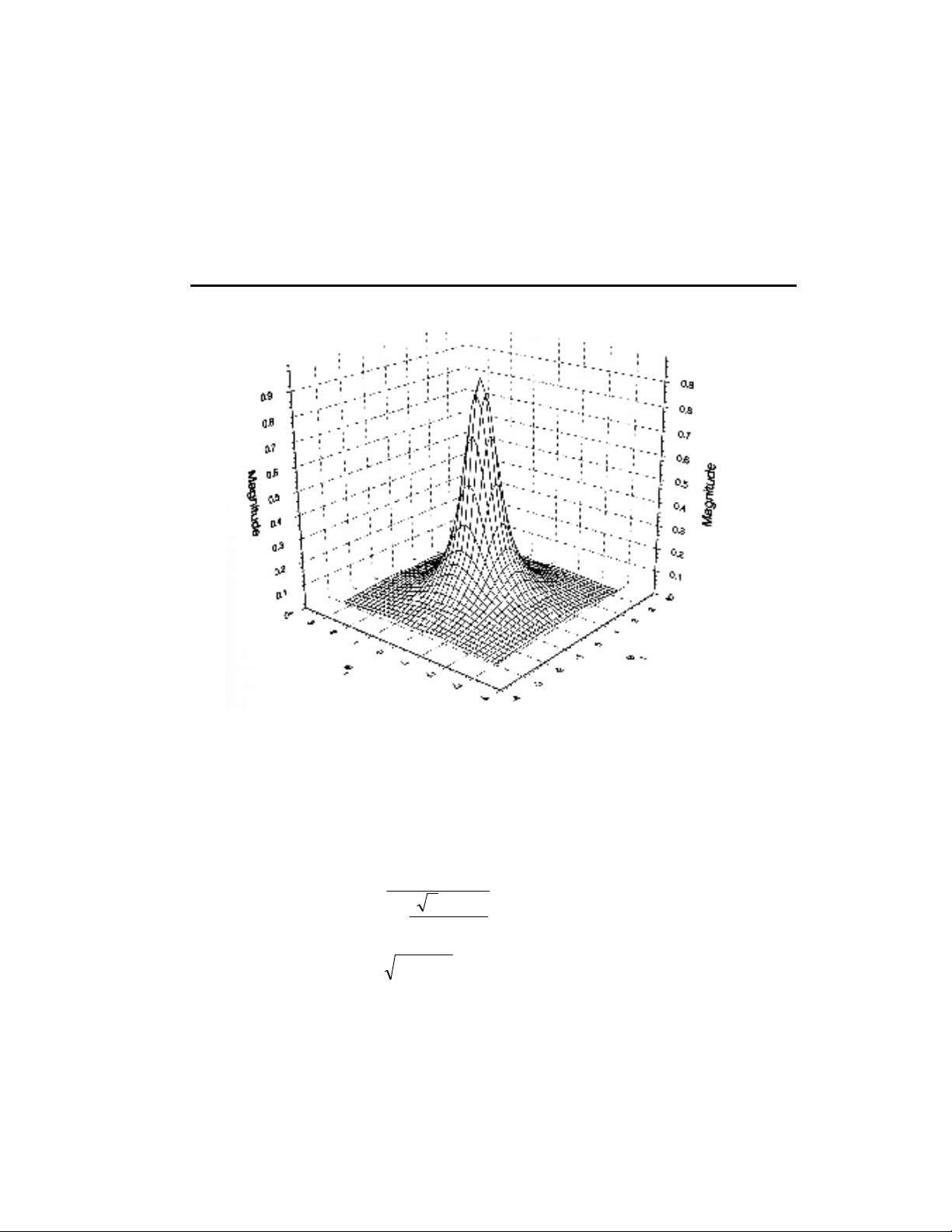
Một ảnh ba chiều của đáp ứng tần số tính từ 11 11 đáp ứng xung
được chỉ trong hình 2.13.
Bảng 2.1 Một phần tư đáp ứng xung của bộ lọc thông thấp D0 =
0.3
0.103591 0.047501 0.017310 0.008810 0.003712
0.002135
0.047501 0.031265 0.014898 0.007494 0.003578
0.001873
0.017310 0.014898 0.009506 0.005306 0.002844
0.001496
26
0.008810 0.007494 0.005306 0.003352 0.001956
0.001102
0.003712 0.003578 0.002844 0.001956 0.001242
0.000743
0.002135 0.001873 0.001496 0.001102 0.000743
0.000473
Hình 2.13 Hình ảnh ba chiều đáp ứng biên độ của bộ lọc thông
thấp.
Ví dụ 2.6 Lặp lại bài toán trước với bộ lọc tuần hoàn đối xứng
Butterworth được cho bởi
),(
)12(
1
1
),(
21
2
0
21
D
D
H
trong đó 2
2
2
121 ),(
D
Giải Thay hàm H(w1,w2) trong chương trình 2.1, như đã giải
thích trong phần cuối của chương trình, chúng ta thu được hệ số
được liệt kê trong bảng 2.2. Đáp ứng tần số được chỉ trong hình