Tuần 8 tiết 16 NS:…………………………ND: ……………………
KIỂM TRA CHƯƠNG I
I. MA TRẬN ĐỀ
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng thấp
Vận dụng
cao
Tổng
TN
TL
TN
TN
TL
TN
TL
1. Hai góc đối đỉnh.
Hai đường thẳng
vuông góc. Góc tạo
bởi 2 đường thẳng
cắt nhau
Nhận biết khái
niệm hai góc đối
đỉnh
Nhận biết khái
niệm đường
trung trực của
đoạn thẳng.
Vẽ được hai
đường thẳng cắt
nhau
Xác định được các
góc đối đỉnh
Vẽ được hình ảnh hai
góc đối đỉnh có số đo.
Số câu
Số điểm
C1, C4c
1đ
C4a
0,5
4
2,5đ
25%
2 . Góc tạo bởi 1
đường thẳng cắt hai
đường thẳng. Hai
đường thẳng s. song.
Tiên đề Ơ-clit.
Định lý. Chứng
minh định lý
Nhận biết được
phát biểu tiên đề
ơ-clit
Nhận biết số đo
góc soletrong
Nhận biết tính
chất hai đường
thẳng song song
-Xác định được định
lý
- Xác định được nội
dung định lý bằng hình
vẽ, GT, KL bằng kí
hiệu
Tính được số đo
góc tạo bởi 1đt cắt
hai thẳng song
song
Chứng minh được
hai đường thẳng
song song, vuông
góc
Giải thích được
hai đường thẳng
vuông góc
Giải thích
được hai
đường
thẳng song
song
Số câu
Số điểm
C2, C3
C 4b
1,5đ
C6
1,5đ
C7, C8b
4đ
C8a
0,5đ
7
7,5đ
75%
Tổng số câu
TS điểm
Tỉ lệ %
5
2,5
25%
3
3,0
30%
2
4,0
40%
1
0,5đ
5%
11
10,0
100%
II. BẢNG MÔ TẢ CHI TIẾT CÁC CÂU HỎI
Câu 1. (NB)Nhận biết được số đo góc đối đỉnh dựa vào tính chất hai góc đối đỉnh
Câu 2. (NB) Nhận biết được cặp góc ở vị trí so le trong khi có một đường thẳng cắt hai đường
thẳng
Câu 3. (NB) Nhận biết đựợc phát biểu của tiên đề Ơ-clit .
Câu 4.a (TH) Xác định được quan hệ từ vuông góc đến song song
Câu 4b (NB) Nhận biết tính chất của hai đường thẳng song song bằng phát biểu
Câu 4c. (NB) Nhận biết khái niệm đường trung trực của đoạn thẳng.
Câu 5. (TH) Vẽ được hình ảnh hai góc đối đỉnh có số đo.
b) (TH) Xác định được các góc bằng nhau dựa trên tính chất của hai góc đối đỉnh.
Câu 6.(VDT) Xác định được hình vẽ, GT, KT của định lý về tính chất hai đường thẳng cùng vuông góc
với một đường thẳng.
Câu 7. (VDT). Tính được số đo góc so le trong, đồng vị, trong cùng phía khi biết1đt cắt hai thẳng
song song và số đo một góc cho trước
Câu 8.a (VDC) Giải thích được hai đường thẳng song song
C8b (VDT) Giải thích được hai đường thẳng vuông góc
III. ĐỀ BÀI
Họ tên ................... ........... Lớp ......
KIỂM TRA 1 TIẾT CHƯƠNG I – HÌNH HỌC 7
I. Trắc nghiệm khách quan (3đ)
ĐỀ 1
Câu 1. Khoanh tròn vào chữ cái đứng trước câu trả lời đúng
Góc xOy có số đo là 1000. Góc đối đỉnh với góc xOy có số đo là:
A. 500. B. 800 . C. 1000 . D. 1200.
Câu 2. Cho hình vẽ sau, Khoanh tròn vào chữ cái đứng trước câu trả lời đúng
Hai góc
22
A và B
ở vị trí là
A. Đồng vị B. So le trong
C. Đối đỉnh D. Trong cùng phía
Câu 3. Điền từ thích hợp vào chỗ trống để được phát biểu đúng về tiên đề Ơ-clit.
“Qua một điểm ở ngoài đường thẳng, ……………. đường thẳng song song với
đường thẳng đó”.
Câu 4. Chọn đúng (Đ), sai (S) cho các nhận định sau
a) Nếu a
b và c
a thì c // b
b) Nếu hai đường thẳng cắt nhau và tạo thành một góc bằng 900 thì hai đường thẳng vuông góc
c) Đường trung trực của đoạn thẳng là đường thẳng vuông góc tại trung điểm của đoạn thẳng đó.
II. Phần tự luận (7 đ)
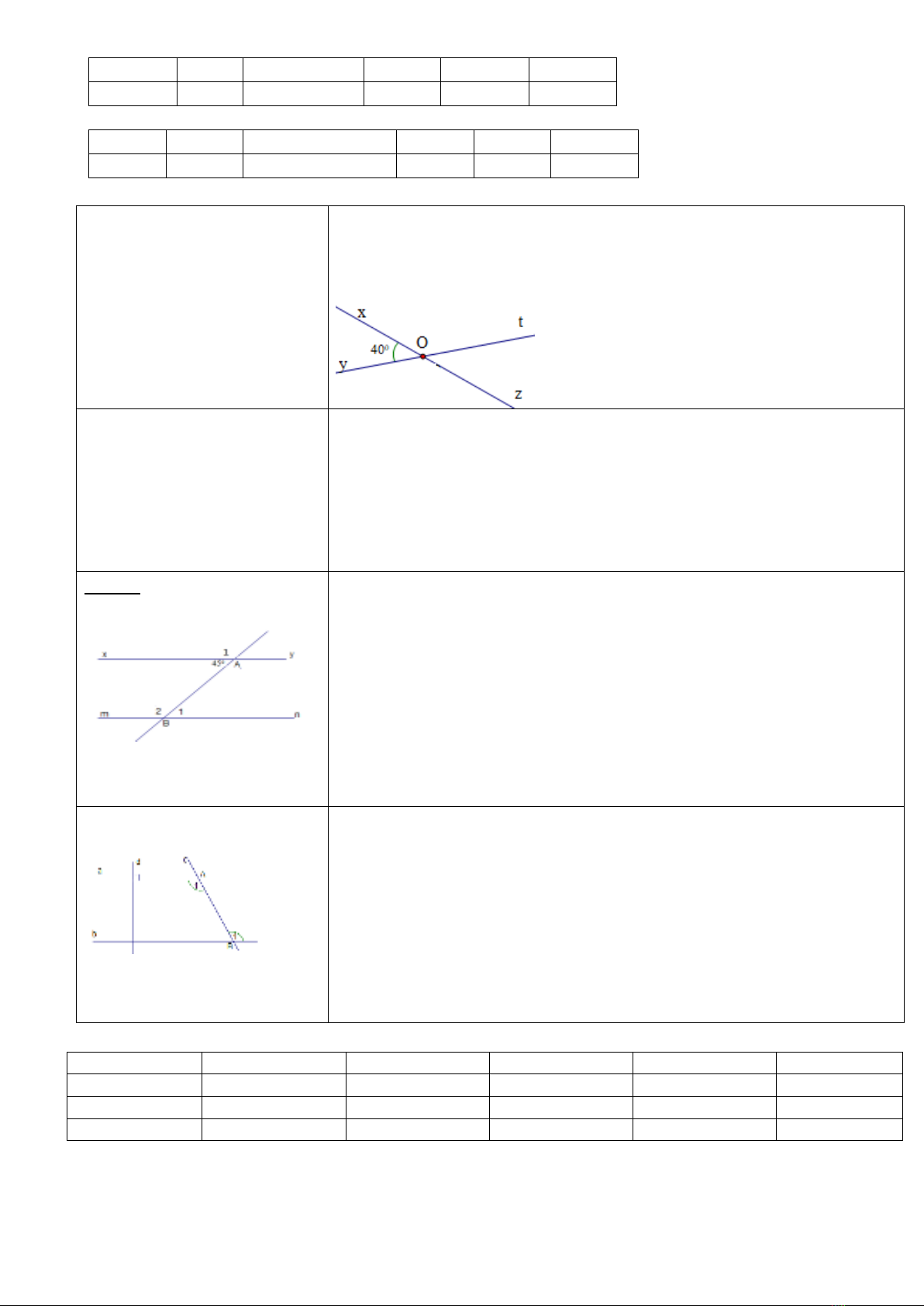
Câu 5 (1đ) Vẽ góc xOy = 400. Vẽ góc tOz đối đỉnh với góc xOy vừa vẽ. Tính số đo góc tOz?
Câu 6. (1,5đ) Hãy vẽ hình, viết giả thiết và kết luận bằng kí hiệu địnhl í: “Nếu hai đường thẳng
phân biệt cùng song song với một đường thẳng thì chúng song song với nhau.”
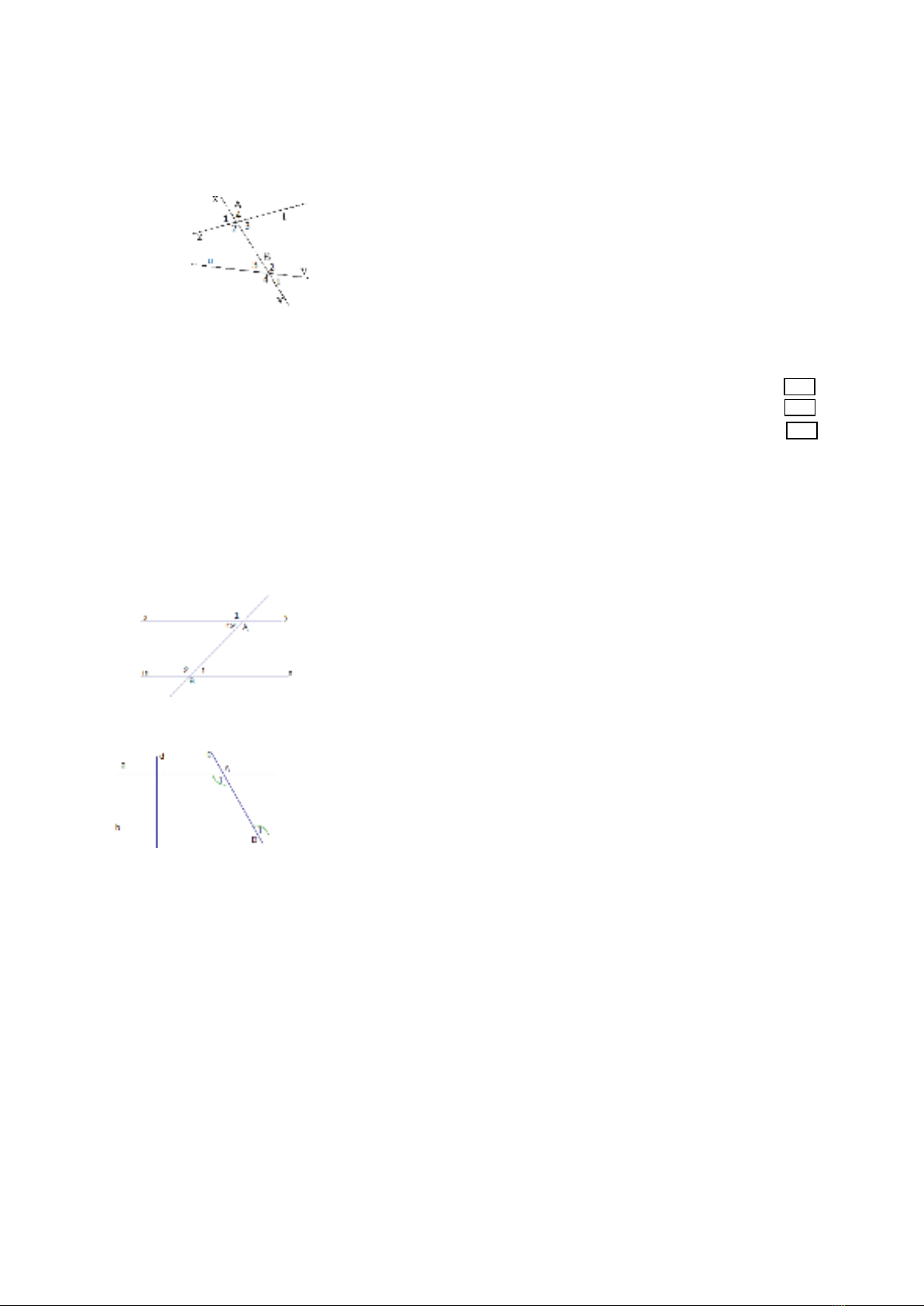
Câu 7.(3đ) Cho hình vẽ sau. Biết xy//mn,
0
xAB 45
Tính số đo các góc
a)
1
B
b)
2
B
c)
1
A
Câu 8. (1,5đ) Cho hình vẽ. Biết
11
AB
.
a) Giải thích vì sao a//b?
b) Đường thảng d và đường thẳng b có vị trí như
thế nào? Vì sao?
Họ tên ................... ........... Lớp ......
KIỂM TRA 1 TIẾT CHƯƠNG I – HÌNH HỌC 7
ĐỀ 2
Câu 1. Khoanh tròn vào chữ cái đứng trước câu trả lời đúng
Góc xOy có số đo là 800. Góc đối đỉnh với góc xOy có số đo là:
A. 500. B. 800 . C. 1000 . D. 1200.
Câu 2. Cho hình vẽ sau, Khoanh tròn vào chữ cái đứng trước câu trả lời đúng
Hai góc
31
A và B
ở vị trí là
A. Đồng vị B. So le trong
C. Đối đỉnh D. Trong cùng phía
Câu 3. Điền từ thích hợp vào chỗ trống để được phát biểu đúng.
“Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng …………….”.
Câu 4. Chọn đúng (Đ), sai (S) cho các nhận định sau
a) Nếu a//b và c
a thì c //b
b) Nếu đường thẳng c cắt hai đường thẳng a//b thì cặp góc so le trong bằng nhau
c) Đường trung trực của đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó.
II. Phần tự luận (7 đ)
Câu 5 (1đ) Vẽ góc xOy = 400. Vẽ góc tOz đối đỉnh với góc xOy vừa vẽ. Tính số đo góc tOz?
Câu 6. (1,5đ) Hãy vẽ hình, viết giả thiết và kết luận bằng kí hiệu địnhl í: “Nếu hai đường thẳng
phân biệt cùng song song với một đường thẳng thì chúng song song với nhau.”
Câu 7.(3đ) Cho hình vẽ sau. Biết xy//mn,
0
xAB 45
Tính số đo các góc
a)
1
B
b)
2
B
c)
1
A
Câu 8. (1,5đ) Cho hình vẽ. Biết
11
AB
.
a) Giải thích vì sao a//b?
b) Đường thảng d và đường thẳng b có vị trí như
thế nào? Vì sao?
IV. ĐÁP ÁN
ĐỀ 1:
Câu 1
Câu 2
Câu 3
Câu 4a
Câu 4b
Câu 4c
C
B
Chỉ có một
Đ
Đ
Đ
ĐỀ 2:
Câu 1
Câu 2
Câu 3
Câu 4a
Câu 4b
Câu 4c
B
A
song song nhau
S
Đ
S
II. TỰ LUẬN
Câu 5 (1đ) Vẽ góc xOy
= 400. Vẽ góc tOz đối đỉnh
với góc xOy vừa vẽ. Tính số
đo góc tOz?
a) Vẽ đúng hình:
- có một góc xOy = 400: 0,25đ
- Vẽ đúng góc đối đỉnh và đặt tên đúng: 0,5đ
- Tính được số đo góc tOx = 400 (đối đỉnh góc xOy) 0,25
Câu 6. (1,5đ) Hãy vẽ
hình, viết giả thiết và kết
luận bằng kí hiệu địnhl í:
“Nếu hai đường thẳng phân
biệt cùng song song với một
đường thẳng thì chúng song
song với nhau.”
Vẽ đúng hình (0,5đ)
Viết đúng GT bằng kí hiệu 0,5đ
Viết đúng kết luận bằng kí hiệu 0,5đ
Câu 7. (3đ) Cho hình vẽ
sau. Biết xy//mn,
0
xAB 45
Tính số đo các góc
a)
1
B
2
b) B
c)
1
A
Vì xy//mn 0,25đ
a)
0
1
B xAB 45
(hai góc so le trong) 0,75đ
b)
0
2
xAB B 180
(hai góc trong cùng phía) 0,5đ
0 0 0 0
2
Suy ra B 180 xAB 180 45 135
0,5đ
b)
0
12
A B 135
(hai góc đồng vị) 1đ
Câu 8. (1,5đ) Cho hình vẽ.
Biết
11
AB
.
a) Giải thích vì sao a//b?
b) Đường thảng d và đường thẳng b có vị trí như thế nào? Vì sao?
ĐA
a) Vì đường thẳng a, b bị cắt bởi c tạo ra cặp góc so le trong
11
AB
nên a//b 0,5đ
b) Vì a//b và
da
nên
db
1đ
Nếu HS chỉ trả lời được vuông góc mà không giải thích được thì
0,5đ
Thống kê điểm
Lớp
G
K
TB
Y
K
Rút kinh nghiệm
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….
…………………………………………………………………………………………………….