8. L ng giác m r ng c a tín hi u ượ ở ộ ủ ệ
8. L ng giác m r ng c a tín hi u ượ ở ộ ủ ệ
M c đích c a ph n này là ch ra làm th nào vesion r i r c c a tín hi u,ụ ủ ầ ỉ ế ờ ạ ủ ệ
chu kỳ T và l y m u kho ng Ts = T/N, có th nhanh chóng t h p tuy n tínhấ ẫ ở ả ể ổ ợ ế
c a hình sin và cosin theo d ng sauủ ạ
x Ah h t
TB h t
T
h
b
N
= − + − −
−
∑( cos( ( ) ) sin( ( ) ) ( )2 1 2 1 1 20
1
π π
Đ i v i t c a Ts chúng ta nhìn th y r ng n u X đánh d u chuy n đ i Fourierố ớ ủ ấ ằ ế ấ ể ổ
c a x, đ ng th nh t (1.17)ủ ẳ ứ ấ
x =
X h
Ncxp i h T
h
N( ) ( ( ) ( )2 1 11 21
1
π
− −
=
∑
S d ng cách Euler, và g i R và I t ng ng ph n th c và ph n o c a X,ử ụ ọ ươ ứ ầ ự ầ ả ủ
đ ng th (1 - 21) s đ c l i nh sau.ẳ ứ ẽ ượ ạ ư
xR
Nht
T
I
Nht
TiR
Nht
T
I
Nht
T
h h
h
N
h h
h
N
= − − − + − − −
= =
∑ ∑
( cos( ( ) ) sin( ( ) )) ( sin( ( ) ) cos( ( ) )2 1 2 1 2 1 2 1
1 1
π π π π
Đ ng nh t th t đúng đ i v i m i x, nh ng có th làm đ n gi n hoá khiồ ấ ậ ố ớ ỗ ư ể ơ ả
x là s th c. Trong tr ng h p đó, chúng ta bi t u tiên là thành ph n o c aố ự ườ ợ ế ư ầ ả ủ
đ ng th c (1.22), ph i tri t tiêu, dùng đ ng nh t th c (1.20) choẳ ứ ả ệ ồ ấ ứ
Ah = Rh / N
Bh = - Ih / N và h ch y t 1 đ n Nạ ừ ế
Bi u th c (1.20) đ c g i là l ng giác m r ng c a xể ứ ượ ọ ượ ở ộ ủ
Ví d 1.6:ụ
Trong ví d sau chúng ta s bi n đ i bi u th c (1.20) cho năm giây vàụ ẽ ế ổ ể ứ
vector ng u nhiên c a 128 nhóm.ẫ ủ
» T = 5 ; % Kho ng th i gian, giâyả ờ
» N = 128; % Chi u dài c a vector ề ủ
» t = linspace (0, T, N + 1);
» t = t (1 : N); % th i gian l y m u ờ ấ ẫ
» x = rand (t); % vector ng u nhiênẫ
» X = stt (x); % DFT c a nó ủ
»A = real (X) / N; % H s cosineệ ố
»B = -imag (X) / N; % H s sinệ ố
»sum cos Zeros (N, N);
»for h = 1 : N
sumcos (h : ) = A (h) * cos (2 * pi * (h - 1) * t/T);
sumsin (h,
= - B (h) * sin (2 * pi * (h - 1) * t/N);
end
» y = sum (sumcos * sumsin);
Bây gi so sánh x và y, đ h a c a chúngờ ồ ọ ủ
» plot (t, x, t, y)
ho c tính sặ ố
» Max (abs (x - y))
Trong version c a chúng ta MATLAB có k t qu là 2.142e - 19ủ ế ả
Ví d 1.7ụ: Phân tích l ng giác c a tín hi u tam giácượ ủ ệ
Bây gi chúng ta mu n phân tích tín hi u tam giác x tính trong ví d 1.5ờ ố ệ ụ
trong thành ph n l ng giác c a nó và ki m tra k t qu . N u ch s N = 512ầ ượ ủ ể ế ả ế ữ ố
xu t hi n trong nhóm ti p theo c a l nh thì r t l n cho b nh c a máy tínhấ ệ ế ủ ệ ấ ớ ộ ớ ủ
c a b n, b n có mu n gi m nó thành s nh , nh 32 ủ ạ ạ ố ả ố ỏ ư
» T = 5;
» N = 512;
» t = linspace (0, T, N + 1); t = (1 : N);
» x1 = 2 * t / T - 1/2 ; x2 = 2 * (T - t) / T - 1/2;
» x = min (x1, x2); % tín hi u tam giác ệ
» plot (t, x)
Chúng ta tính h s c a sines và cosine.ệ ố ủ
» X = fft (x);
» A = real (X) / N; % h s cosineệ ố
» B = - imag (X) / N); % h s sineệ ố
» sumcos = zeros (N, N);
» sumsin = zeros (N, N);
» for h = 1 : N
sumcos (h, : ) = A(h) * cos (2 * pi * (h - 1) * t/T);
sumsin (h, : ) = B (h) * sin (2 * pi * (h - 1) * t/T);
end
» y = sum (sumcos + sumsin);
Chúng ta có th ki m tra các k t qu b ng cách so sánh x và y, đ h a c aể ể ế ả ằ ồ ọ ủ
chúng
» plot (t, x, t, y);
và s ố
»max (abs (x - y))
9. Nh ng tín hi u t n s cao và ký hi u:ữ ệ ầ ố ệ
9. Nh ng tín hi u t n s cao và ký hi u:ữ ệ ầ ố ệ
hình 1.12 đã ch ra s t ng ng gi a công su t c a tín hi u và bi nỞ ỉ ự ươ ứ ữ ấ ủ ệ ế
đ i Fourier c a nó đ i v i các t n s đ n t n s Nyquist. Đi u này trổ ủ ố ớ ầ ố ế ầ ố ề ở
nên thú v đ xem đi u ị ể ề gì x y ra khi chúng ta l y m u t i kho ng th iả ấ ẫ ạ ả ờ
gian Ts h ng s tín hi u tu n hoàn liên t c c a t n s cao đ n t n sằ ố ệ ầ ụ ủ ầ ố ế ầ ố
Nyquist Nf = 1/ (2Ts). Nh chúng ta nhìn th y đây, version l y m u c aư ấ ở ấ ẫ ủ
tín hi u đ ng nh t v i tín hi u khác t n s th p. Hi n t ng này g i làệ ồ ấ ớ ệ ầ ố ấ ệ ượ ọ
d u hi u t Cấ ệ ừ 1 , t ý nghĩa Latin “other”, nh ng cái khác. Đ nh n m nh ýừ ữ ể ấ ạ
này chúng ta ch n T là 5ọ giây, N = 16 l y m u trong m t chu kỳ, và hi n raấ ẫ ộ ệ
theo kho ng l y m u v i Ts = T/N và t n s m u v i fs > 1/Ts.ả ấ ẫ ớ ầ ố ẫ ớ
Tín hi u tu n hoàn v i chu kỳ T có cệ ầ ớ hu kỳ c b n c a T n i T/k v i kơ ả ủ ố ớ
phù h p. Chúng ta ch ra t n s c a nó k/T, v i f nh . Cũng nh tín hi u, choợ ỉ ầ ố ủ ớ ỏ ư ệ
kho ng cách sin (2ảπft) và cos (2πft). T n s f có th luôn vi t nh sauầ ố ể ế ư
f = fapp + nfs
Trong đó n và s nguyên và 0 ố≤ |fapp| < Nf. Nó d dàng ki m tra r ng t iễ ể ằ ạ
các t b i s c a Ts nh sau ộ ố ủ ư t = hTs, sin (2πft) = sin (2πfappt). Th c t ự ế
sin(2πft) = sin (2π (fapp + nfs) t)
= sin (2π (fapp + nfs) hTs)
= sin (2π (fapp hTs + 2πnfshTs)
= sin (2π (fapp hTs + 2πnh)
= sin (2π fapp)
Song tín hi u ệx = sin(2
π
ft), t n s f, khi l y m u t n s fs, là không th phânầ ố ấ ẫ ở ầ ố ể
bi t đ c t tín hi u xệ ượ ừ ệ 1 = sin(2πfappt) c a t n s th p fủ ầ ố ấ app MATLAB cho phép
chúng ta gi i quy t v n đ và bi u di n các d u hi u. ả ế ấ ề ể ễ ấ ệ Hãy dùng m t p sau;ệ
alias.m:
T = 5 ; % t n s c b nầ ố ơ ả
Np = 512; %S đi m đ ch mố ể ể ấ
t = linspace(0,T,Np+1;
t = t(1:Np); % tìm đ phân gi i c a th i gian ộ ả ủ ờ
%đ ch m đi m ể ấ ể
N=16; % s đi m l y m uố ể ấ ẫ
Ts =T/N; % kho ng l y m uả ấ ẫ
fs =1/Ts; % t n s l y m uầ ố ấ ẫ
ts = Ts*(0:(N-1)); % kho ng th i gian l y m uả ờ ấ ẫ
Nf = 1/(2*Ts); % T n s Nyquistầ ố
f = k/T; % t n s liên t cầ ố ụ
% tín hi uệ
x = sin(2*pi*f*t); % tín hi u, đ phân gi i caoệ ộ ả
xs = sin(2*pi*f*ts); % tín hi u, l y m u phân gi iệ ấ ẫ ả
% tìm fapp, nh sau: f =n*fs+fappư
n = round(f/fs);
fapp = f-n*fn;
xa = sin(2*pi*fapp*t);
plot(t,[x;xa],ts,xs,'0');
str1 = ['fs = ', num2str(fs), 'Nf = ',num2str(Nf)];
str2 = ['k = ', num2str(k), 'f = ',num2str(f)];
str3 = [fapp=', num2str(fapp)];
str = [str1, ' ' ,str2, ' ', str3];
title(str);
Ch y chúng v i l nh sauạ ớ ệ
» k= 17; alias
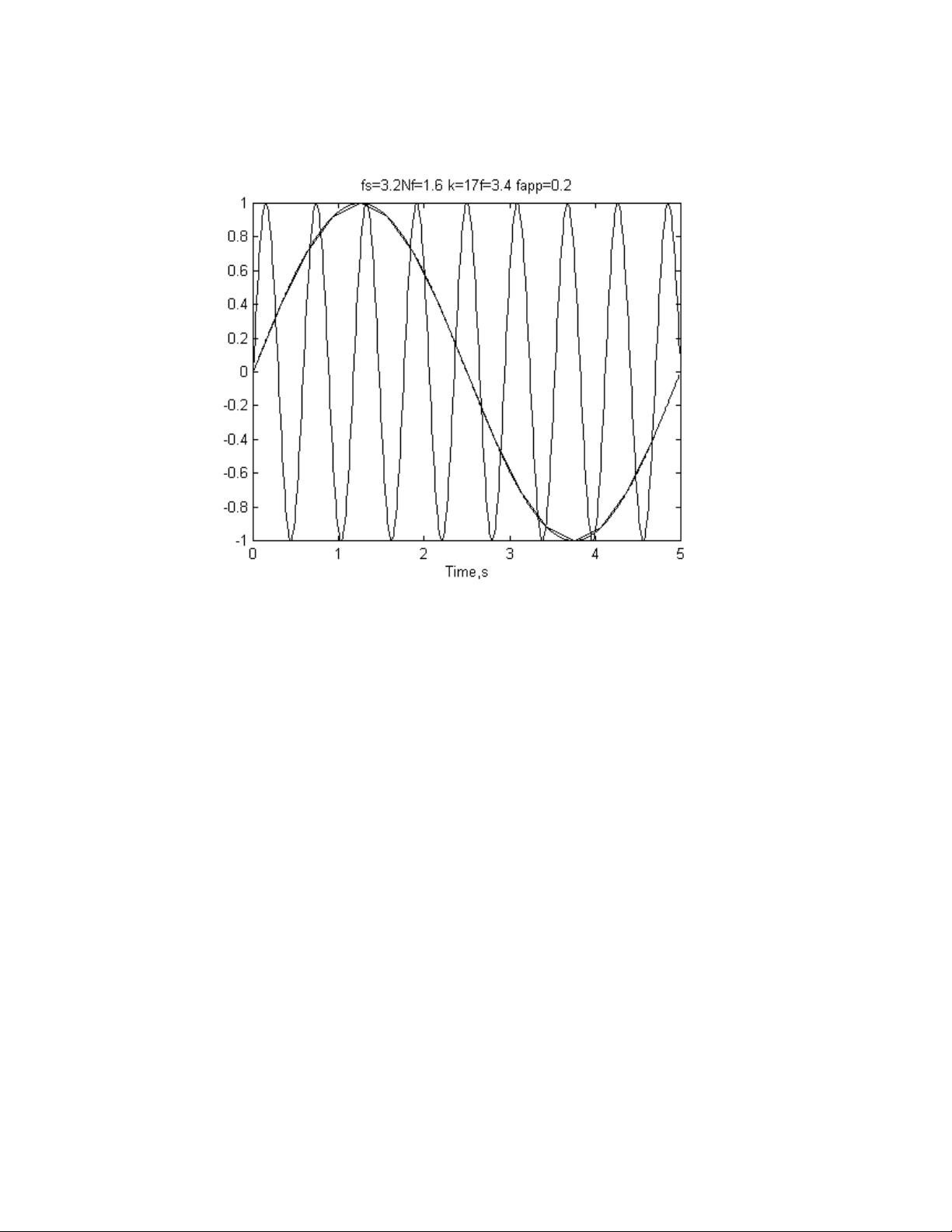
Hình 1.17 tín hi u t n s cao l y m u nh m t t n s th p.ệ ầ ố ấ ẫ ư ộ ầ ố ấ
Ví d 1.8:ụ Giao đ ng c a m t t mộ ủ ộ ấ
Vi c tính toán ví d 1.5 và 1.7 có th có m t ng d ng k thu t mô tệ ở ụ ể ộ ứ ụ ỹ ậ ả
trong: Máy ki m tra giao đ ng. Ví d đ n gi n có d ng nh hình 1.17. Các bể ộ ụ ơ ả ạ ư ộ
ph n ho t đ ng c a máy là 4 tr c quay, không có kh i l ng giao đ ng mậ ạ ộ ủ ụ ố ượ ộ 1 đ nế
m4. Nh mô t trên hình1.17 (a), kh i l ng không giao đ ng có th đo nư ả ở ố ượ ộ ể ạ
c a vòng trong làm b ng s t (thép) và t a trên đĩa quay. Kh i l ng mủ ằ ắ ự ố ượ 1 và m2
b ng nhau, nh ng quay theo hai h ng đ i nhau, và cũng nh v y đ i v i kh iằ ư ướ ố ư ậ ố ớ ố
l ng mượ 3 và m4. M t trong nh ng b ph n đ c ch chi ti t trên hình 1.17 (b).ộ ữ ộ ậ ượ ỉ ế
Cho r ng kho ng cách gi a tr c quay qua đi m 0 và tâm c a kh i l ng khôngằ ả ữ ụ ể ủ ố ượ
giao đ ng, mội là ri . Gi s kh i l ng quay quanh đi m 0 v i t c đ ả ử ố ượ ể ớ ố ộ ωi. L cự
h ng tâm đ t vào tâm c a kh i l ng không giao đ ng b ng ướ ặ ủ ố ượ ộ ằ Fi = miri
ω
2i.
N u chuy n đ ng b t đ u t tr c th ng đ ng OA và h ng quay theo chi uế ể ộ ắ ầ ừ ụ ẳ ứ ướ ề
kim đ ng h , sau th i gian t góc gi a OA và h ng c a ồ ồ ờ ữ ướ ủ F =
ω
it. Thành ph nầ
th ng đ ng c a l c h ng tâm là ẳ ứ ủ ự ướ Fv = miri
ω
2i.cos
ω
it, và thành ph n n m ngangầ ằ
là Fh = miri
ω
2i.sin
ω
it . Đ i v i kh i l ng bên ph i đây b ng kh i l ng màố ớ ố ượ ả ở ằ ố ượ
quay h ng ng c, b t đ u t tr c đ ng.ướ ượ ắ ầ ừ ụ ứ
Nó s đ t l c h ng tâm khi mà thành ph n th ng đ ng ẽ ặ ự ướ ầ ẳ ứ = Fv, khi thành
ph n ngang = ầ-Fh. Thành ph n n m ngang giao đ ng quanh đi m, khi thànhầ ằ ộ ể
ph n th ng đ ng lên caoầ ẳ ứ , sinh ra l c đàn h i ự ồ = 2 miri
ω
2i . cos
ω
it. Đi u quanề