
Practice Questions Answers and Explanations
1. Choice ais correct. The word and indicates a decimal point. Therefore, the decimal point should go
after five hundred twelve and before sixteen thousandths. The number 16 must end in the thousandths
place, which is three digits to the right of the decimal. The correct answer is 512.016.
Choice bis “five hundred twelve and sixteen hundredths.”
Choice cis “five hundred twelve thousand, one hundred sixty.”
Choice dis “fifty one and two hundred sixteen thousandths.”
Choice eis “five hundred twelve and sixteen ten thousandths.”
2. Choice fis correct. First, change the fractional parts of the problem to have the common denominator
of 12.
4
1
4
2
−1
1
9
2
Subtract the numerators. Since 4 is less than 9, you must borrow one whole from the whole number 4.
This means that you are adding
1
1
2
2
to the first fraction.
3
1
1
6
2
−1
1
9
2
.
Subtract the fractional parts then the whole numbers. The final answer is 2
1
7
2
.
3. Choice bis correct. The correct order of operations must be used to simplify the expression. You may
remember this as PEMDAS or “Please Excuse My Dear Aunt Sally.” The P stands for parentheses or any
grouping symbol. Absolute value is a grouping symbol, so it will be done first.
|−8| + 4 ×23=
8 + 4 ×23
Next, perform the exponent part.
8 + 4 ×8
Then, the multiplication.
8 + 32
Last, the addition.
The final answer is 40.
4. Choice gis correct. This problem can be approached a couple of different ways. The simplest way
might be to look at multiples of 4 and 5 until the multiples add to 18. If both 4 and 5 are multiplied by
2, they become 8 and 10. 8 plus 10 is 18. Therefore, there are 8 boys and 10 girls in the class.
The problem can also be done with an equation.
4x+ 5x= 18
When solved, x= 2. Multiply 4 by 2 to find that there are 8 boys.
–ACT MATH TEST PRACTICE–
184
5. Choice cis correct. To find the median, place the numbers in order from least to greatest and find the
middle number. In order, the numbers are:
0.008, 0.024, 0.024, 0.095, 0.1, 0.3
Since there are an even number of numbers, there are two middle numbers (0.024 and 0.095). Take the
average of these two middle numbers by adding them and dividing the sum by two. The answer is
0.0595.
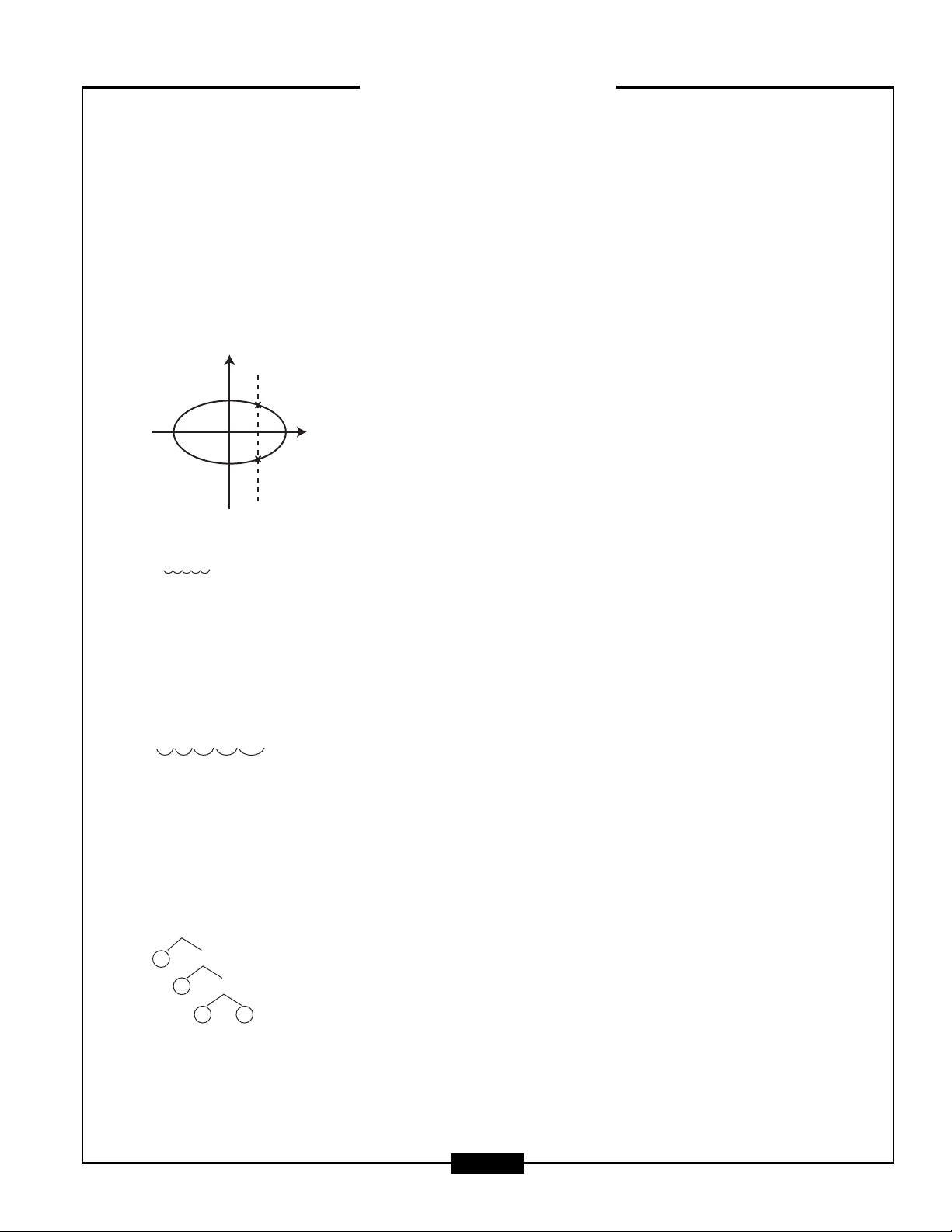
6. Choice his correct. Use the vertical line test to see if each graph is a function. A graph is NOT a func-
tion if vertical lines drawn through the graph hit the graph more than once.
7. Choice dis correct. When multiplying by 105you move the decimal point 5 places to the right.
The answer is 460,000.
Another way to look at the problem is to recognize that 105= 100,000 and multiply 4.6 by 100,000.
The answer is 460,000.
8. Choice gis correct. 35= 3 ×3 ×3 ×3 ×3 = 243. The answer is 243.
9. Choice ais correct. Consecutive odd integers starting with 3 are being added to find the next number.
Therefore, 11 must be added to 24 to find the next number. The answer is 35.
You may also notice that the numbers can be found using the expression n2−1 where nis the place in
the pattern. We are looking for the sixth number, so n= 6. 62−1 = 35. The answer is 35.
10. Choice his correct. First, you can eliminate choices fand ibecause they contain numbers that are not
prime. Next, use a factor tree to determine the prime factorization.
The prime factorization of 84 is 2 ×2 ×3 ×7, which can be written in exponential notation as 22×3 ×
7. The answer is 22×3 ×7.
84
242
76
32
0, 3, 8, 15, 24, . . .
+3 +5 +7 +9 +11
4.60000. = 460,000
–ACT MATH TEST PRACTICE–
185

11. Choice cis correct. To easily see the slope, change the equation into the form y= mx + b. The equation
is then y=
7
3
x+ 3. The coefficient of xis the slope.
7
3
is the answer.
12. Choice fis correct. The perimeter is twice the width plus twice the length: P= 2w+ 2l. Insert 20 for P
and 4 for w, then solve for l.
20 = 2(4) + 2l
20 = 8 + 2l
20 −8 = 2l
12 = 2l
6 = l
6 is the length.
13. Choice eis correct. Find the lengths of the unlabeled sides by comparing them to the given sides.
Divide the shape into two rectangles as shown below. Find the area of each of the regions and add
together to find the total area.
30 + 28 = 58 sq in.
14. Choice gis correct. Find the cost for one can (unit rate) by dividing the cost of five cans by 5. $6.50 ÷ 5
= $1.30 per can. Multiply the cost per can by 9 cans. $1.30 ×9 = $11.70. Nine cans cost $11.70.
A proportion can also be used:
$6
5
.50
=
9
x
.
To solve the proportion, cross-multiply and divide.
5x= $58.50
5
5
x
=
$58
9
.50
x= $11.70
15. Choice cis correct. Find a common denominator (15x). Multiply the first fraction by
5
5
and the second
fraction by
3
3
x
x
. The result is
1
1
5
0
x
+
1
3
5
x
x
=
10
1
+
5x
3x
. The answer is
10
1
+
5x
3x
.
16. Choice iis correct. The endpoints are on −1.5 and 0, so the possible choices are iand h. The endpoints
are open dots (not solid) and, therefore, only < or > signs can be used (not ≤or ≥). This information
narrows the answer choices down to only i.
17. Choice cis correct. First, raise everything in the parentheses to the second power: −(62(x4)2y3)2).
When you have a power to a power you multiply the exponents. Thus, −(36x8y6). Apply the negative
for the final answer of −36x8y6.
10 in
7 in
4 in
3 in
30
28
–ACT MATH TEST PRACTICE–
186

18. Choice his correct. Use substitution to solve for xand y. First, solve the second equation for y.
y= 4x−47
Next, substitute the above value for yinto the first equation and solve for x.
2x+ 3(4x−47) = 55
2x+ 12x−141 = 55
14x−141 = 55
14x= 196
x= 14
Now, substitute 14 for xin the second equation and solve for y.
4(14) = y+ 47
56 = y+ 47
y= 9
The solution to the system of equations is (14, 9). The problem asks you to find x−y.
14 −9 = 5.
The answer is 5.
19. Choice eis correct. First, eliminate choice dbecause the dot on the graph is open and therefore the
inequality sign must be either < or > (not ≤or ≥). Next, solve each inequality for xremembering that
the inequality symbol must be flipped when multiplying or dividing by a negative. The answer choices
become:
a. x> 0
b. x< −
1
4
c. x< −4
e. x> −4
The endpoint is on −4, so the only possibilities are choices cand e. The arrow points to numbers
greater than −4. The answer is choice e.
20. Choice fis correct. Notice that you are taking the cube root, not the square root. Break up the expres-
sion under the radical into perfect cubes.
3(8)(2)x
3x2y3y
Any exponent divisible by 3 is a cube root. Take out the perfect cubes and leave everything else under
the radical.
2xy
32x2y
is the answer.
21. Choice cis correct. Substitute the value 63° for C.
F=
5
9
(63) + 32
F= 35 + 32
F= 67
The answer is 67°F.
–ACT MATH TEST PRACTICE–
187

22. Choice his correct. The equation is quadratic, so there are two ways to solve it. First, try to factor the
left-hand side of the equation. Since it is factorable, solve the equation using factoring.
x2+ 8x+ 15 = 0
(x+ 5)(x+ 3) = 0
Set each of the factors equal to zero and solve for x.
x+ 5 = 0 x+ 3 = 0
x= −5x= −3
The solution set is {−5, −3}.
The quadratic equation can also be used to solve the equation.
x=
x=
x=
x=
−8
2
±2
x=
−8
2
+2
x=
−8
2
−2
x=
−
2
6
= −3x=
−
2
10
= −5
The solution set is {−5, −3}.
23. Choice bis correct. Solve the equation for musing inverse operations.
5k= 9m−18
5k+ 18 = 9m
5k+
9
18
= m
Since this answer does not appear as one of the choices, you must determine if any of the choices are
equivalent to it. If you divide each of the numerator terms by 9 you get
5
9
k+ 2 = m, which is choice b.
24. Choice his correct. Solve the equation by moving all xterms to one side.
5x−5x−7 = 5x−5x+ 10
−7 = 10
−7 ≠10
Ø
The x’s cancel, leaving −7 = 10, which is not true. Since −7 never equals 10, there is no solution.
25. Choice eis correct. Factor the numerator.
(4x−
x
1
+
)(
3
x+3)
Use the denominator as a clue when factoring the numerator. Most likely, the denominator will be one
of the factors in the numerator.
Cancel the x+ 3 in the numerator with the x+ 3 in the denominator. This leaves 4x−1.
−8 ± 64 −60
2
−8 ± (8)2−
(4)(1)(
15)
2
−b±b2−4a
c
2a
–ACT MATH TEST PRACTICE–
188












![Từ vựng tiếng Anh về thức ăn và giảm cân [mới nhất, đầy đủ]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251217/nglinh.diamond@gmail.com/135x160/53091766028543.jpg)


![Tài liệu Từ vựng tiếng Anh Trung cấp [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250913/nguyentuan250421@gmail.com/135x160/99491757910839.jpg)
![Tài liệu Từ vựng Tiếng Anh theo chủ đề [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250913/namdhuet@gmail.com/135x160/83251757753810.jpg)



![Tài liệu Từ vựng tiếng Anh cho bé [chuẩn nhất/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250731/huadaithesang2509@gmail.com/135x160/18631754013896.jpg)





