» b = 1 : N; % bins
» Ts = 1/128; % Kho ng l y m u theo giâyả ấ ẫ
» fs = 1/Ts; % T n s l y m u theo Hzầ ố ấ ẫ
» ts = Ts x (b - 1) % Kho ng l y m u ả ấ ẫ
» a1 = 7 ; f1 = 16;
» x1 = a1 * sin (2 * pi * f1 * ts) ; % tín hi u đ uệ ề
» a2 = 3; f2 = 48
» x2 = a2 * sin (2 * pi * f2 * ts) ; % tín hi u th haiệ ứ
» x = x1 + x2;
N u b n nhìn th y k t qu tín hi u (hình 1.13) đ a l nh sau vàoế ạ ấ ế ả ệ ư ệ
» plot (ts, x)
» xlabel (‘Time, s’) , y label (‘x’)
Chúng ta có th xây d ng và ch m đi m c a ph công su t.ể ự ấ ể ủ ổ ấ
» X = fft(x); % DFT c a xủ
» pwr = x * cosj (X) / N % Công su t c a tín hi uấ ủ ệ
» frs = (b = 1), N * fs % Các t n sầ ố
» Plot (frs, pwr) % ch m đi m ph công su tấ ể ổ ấ
K t qu ch m đi m trên hình 1.14. Tín hi u xế ả ấ ể ở ệ 1 đ t công su t đi mạ ấ ở ể
65, v i t n s fớ ầ ố 1 = 16H2 (65 = 1 + 512 x 16 / 128) và bin 449, ph n ch m h nở ầ ậ ơ
vì liên h p c a s tín hi u 65 = 1 + 65 đ c c t trong bin 449 = 1 + 512 - 64ợ ủ ố ệ ượ ấ
HìnhI.15 Ph năng l ng c a tín hi u x=x1+x2ổ ượ ủ ệ
129
Ph công su t đ c ch ra trên hình 1.14. Ta có th ki m tra ổ ấ ượ ỉ ể ể pwr (65) =
(a1/2)2.N. T ng t nh v y đ i v i tín hi u xươ ự ư ậ ố ớ ệ 2. Công su t bin 193 và 321 và ấ ở
pwr (193) = pwr (321) = (a2/2)2 N
Ví d 1.5ụ: Nh n d ng t n s và thành ph n công su t chínhậ ạ ầ ố ầ ấ
Trong thí d này chúng ta s phân tích tín hi u tam giác c a chu kỳ S = 5ụ ẽ ệ ủ
giây và đi m nh y biên đ 1 vào thành ph n t n s c a chúng s d ng 512ể ả ộ ầ ầ ố ủ ử ụ
đi m l y m u. Chúng ta quan tâm đ n vi c tìm ph n trăm nào c a công su tể ấ ẫ ế ệ ầ ủ ấ
t ng là thành ph n trong tín hi u đ c nh n t g c, b ng cách tách các thànhổ ầ ệ ượ ậ ừ ố ằ
ph n t 4 thành ph n. Chúng ta còn mu n bi t b ng cách nào làm x p x tínầ ừ ầ ố ế ằ ấ ỉ
hi u v i tín hi u chu n. Đ u tiên, chúng ta xây d ng ph ng án r i r c x c aệ ớ ệ ẩ ầ ự ươ ờ ạ ủ
tín hi u b ng l y m u nó t i 512 đi m b ng nhau.ệ ằ ấ ẫ ạ ể ằ
» T = S;
» N = 512;
» t = linspace (0,T, N + 1) ; t = (1 : N);
» x1 = 2 * t/T - 1/2 ; x2 = 2*(T - t) / T - 1 / 2;
» x = min (x1, x2); % tín hi u tam giác và xây d ng ph công su t c aệ ự ổ ấ ủ
chúng:
» b = 1 : N % Kho ng l y m u và t n sả ấ ẫ ầ ố
» X = fft (x);
» Ts = T / N ; fs = N/T % b ng (b - 1) / N * fsằ
» prw = X * conj (X) / N;
Đ ki m tra k t qu c a chúng ta, chúng ta có th dùng đ ng th cể ể ế ả ủ ể ẳ ứ
Parseval. Nh ng s sau ph i b ngữ ố ả ằ
»[sum (pow) norm (x)^ 2]
ans =
42.668042.6680
D dàng nh n th y các t n s này g m thành ph n l n nh t c a côngễ ậ ấ ầ ố ồ ầ ớ ấ ủ
su t, s d ng hàm ấ ử ụ sort v i quay tr l i các ph n t c a ớ ở ạ ầ ử ủ pow b ng cách tăngằ
đi m:ể
» [spow, spos] = sort (pow);
Chúng ta tìm ch s c a 4 t n s thành ph n công su t l n nh t:ữ ố ủ ầ ố ầ ấ ớ ấ
» m = 4; spos (N: -1 : (N - m + 1)
Chúng ta có th th y các t n s này c u thành trên 512, 2, 510 và 4. Bâyể ấ ầ ố ấ
gi chúng ta xây d ng tín hi u x p x ờ ự ệ ấ ỉ
» X4 = zesos (X); % Vùng đ x p x Xổ ấ ỉ
» h = [512 2 510 4];
» X4 (h) = X (h); % chép binh c u thành công su t caoầ ấ
130
Ph n trăm c a công su t t o thành trên 4 thành ph n ch đ o đ c đ a raầ ủ ấ ạ ầ ỉ ạ ượ ư
b iở
» pere = 100 * (norm (X4) / norm (X))^2
K t lu n, 99,7698 % c a công su t đ c t o thành trên 4 nhóm, t ngế ậ ủ ấ ượ ạ ươ
ng v i t n s c b n 0.2 Hz; liên quan đ n bin s 2, t n s truy n đ t c a nóứ ớ ầ ố ơ ả ế ố ầ ố ề ạ ủ
liên quan đ n bin 512, giao đ ng th 2, 0.6 Hz liên quan đ n bin s 4, và h sế ộ ứ ế ố ệ ố
truy n c a nó, liên quan đ n bin 510. Chúng ta s s d ng k t q a trong ví dề ủ ế ẽ ử ụ ế ủ ụ
1.8
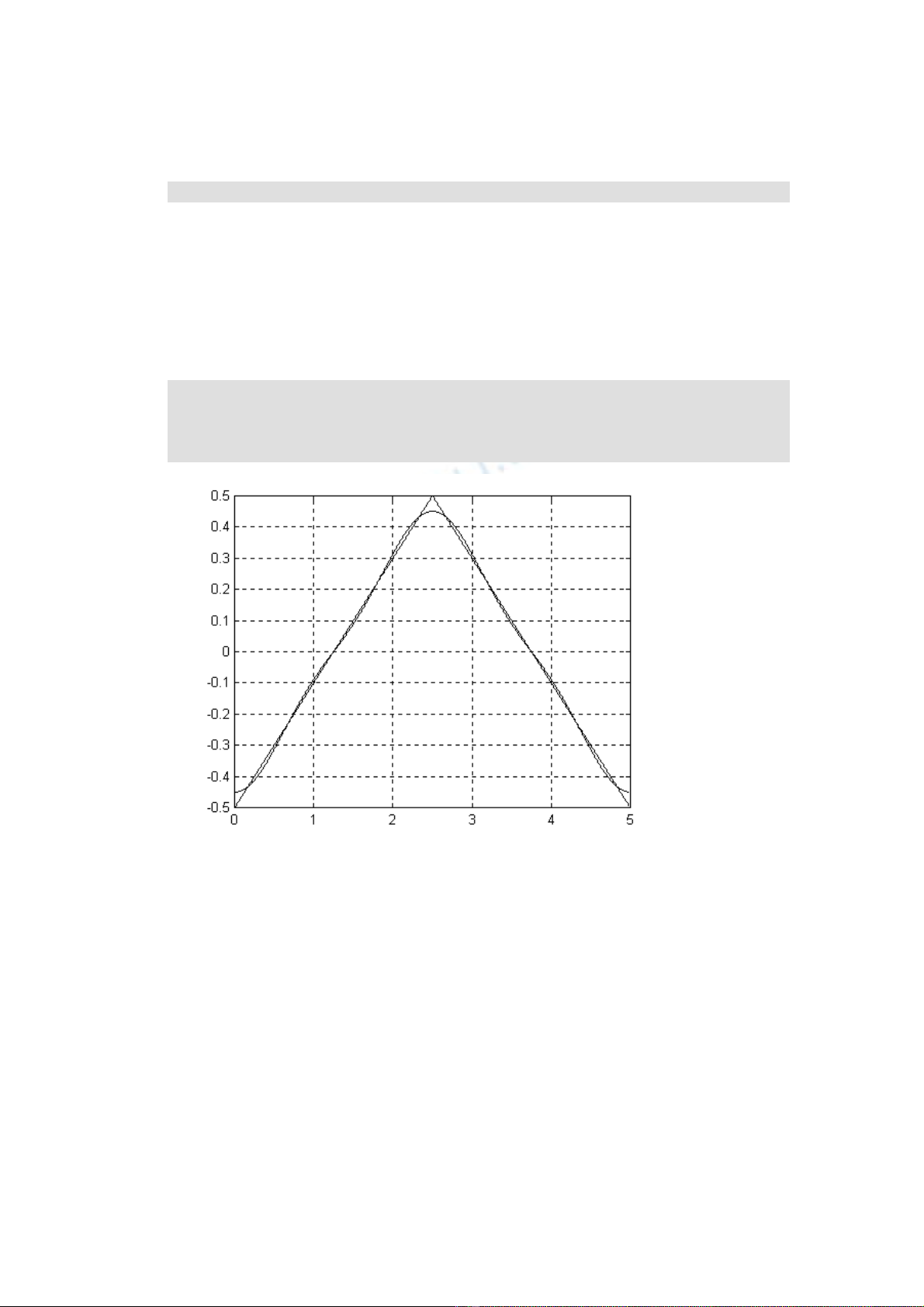
Nh ng dòng sau s ch ra làm th nào ti n g n đ n tín hi u tam giác gócữ ẽ ỉ ế ế ầ ế ệ
đ c x p x , xem hình 1.15ượ ấ ỉ
» x4 = ift (X4);
» plot (f, [x; x4]) , grid
» xlabel (‘ t ’), ylabel (‘ Tín hi u tam giác và s x p x chú ý)ệ ự ấ ỉ
Hình I.16. S x p x c a tín hi u hình tam giácự ấ ỉ ủ ệ
131