CH NG 2ƯƠ
MÔ HÌNH E-R
NHÓM 1
Tr n Ng Bìnhầ ự
Tô Thanh H iả
Tr n Văn Longầ
Đoàn Th Thu Minhị
Nguy n Đ c Tu nễ ứ ấ
N I DUNG TRÌNH BÀYỘ
GI I THI U MÔ HÌNH ERỚ Ệ
CÁC THÀNH PH N C B NẦ Ơ Ả
T p th c th ậ ự ể
M i quan h gi a các t p th c thố ệ ữ ậ ự ể
PHÂN LO I M I QUAN HẠ Ố Ệ
M i quan h nh nguyênố ệ ị
M i quan h Is-aố ệ
M i quan h ph n xố ệ ả ạ
M i quan h đa nguyênố ệ
GI I THI UỚ Ệ
Mô hình E-R đ c đ xu t b i P. Chen ượ ề ấ ở
(1976). Đây là m t mô hình ộm cứ khái ni mệ
d a vào vi c nh n th c th gi i th c thông ự ệ ậ ứ ế ớ ự
qua t p các đ i t ng đ c g i là các th c ậ ố ượ ượ ọ ự
th và các m i quan h gi a các đ i t ng ể ố ệ ữ ố ượ
này.
Bi u di n d i d ng s đ ERể ễ ướ ạ ơ ồ
Th c thự ể (entity) là m t v t th t n t i và ộ ậ ể ồ ạ
phân bi t đ c v i các v t th khác. ệ ượ ớ ậ ể
M t nhóm bao g m các th c th “t ng ộ ồ ự ể ươ
t ” nhau t o thành m t ự ạ ộ t p th c thậ ự ể
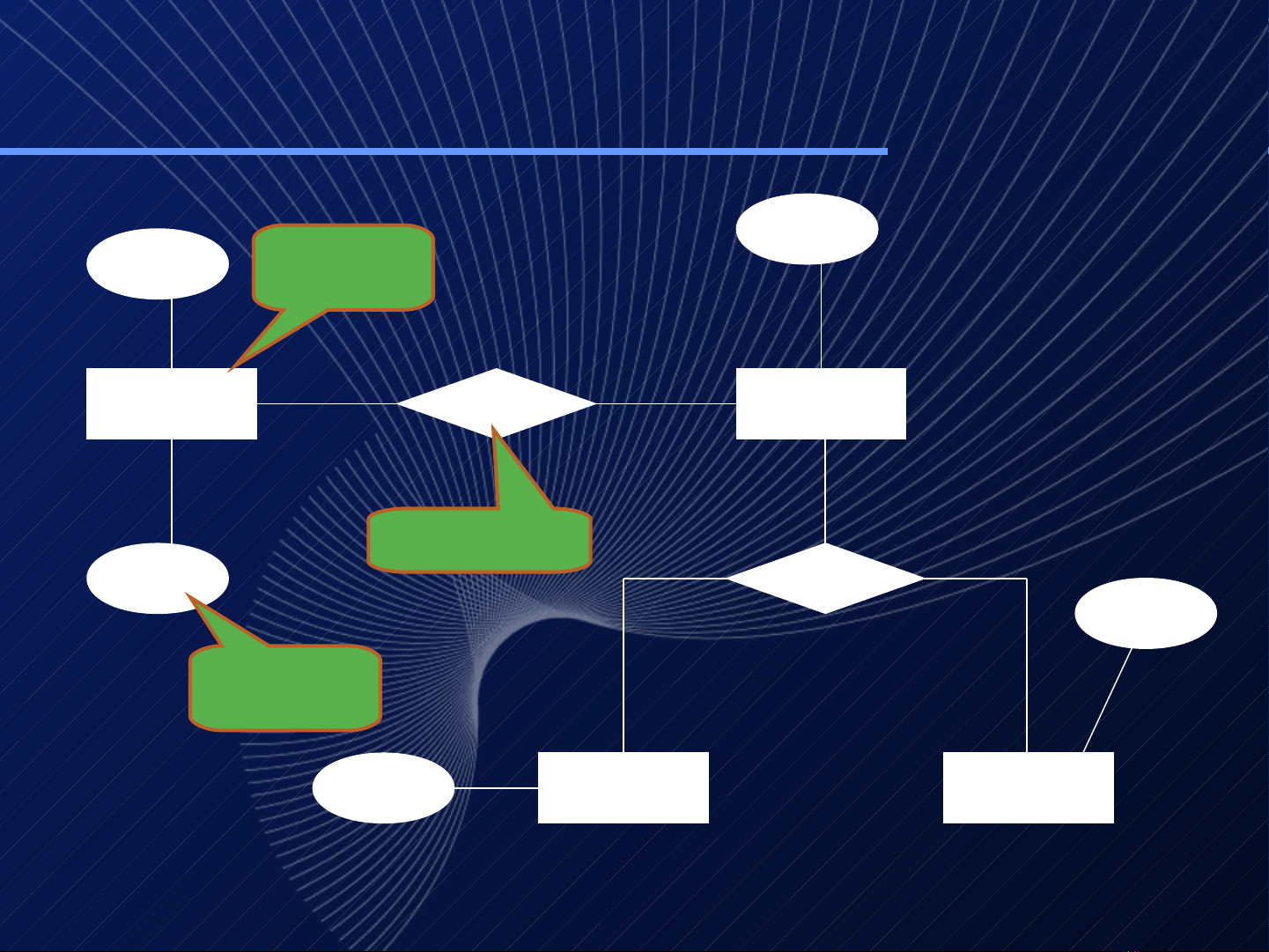
MÔ HÌNH E-R THƯỜNG Đ C BI U DI N ƯỢ Ể Ễ
D I D NG S Đ (S Đ E – R).ƯỚ Ạ Ơ Ồ Ơ Ồ
Mô hình ER (s đ ER)ơ ồ
Các t p ậ
th c thự ể
M i quan ố
hệ
Thu c ộ
tính
T p th c thậ ự ể
Các m iố quan h : is-a (k th a), ph n x , nh ệ ế ừ ả ạ ị
nguyên 1-1/ 1-n/ n-n, đa nguyên.
CÁC THÀNH PH N C B NẦ Ơ Ả