CHƯƠNG 3: MÔ HÌNH HOÁ MÁY ĐIỆN KHÔNG ĐỒNG BỘ
§1. MÔ HÌNH MẠCH CỦA M.Đ.K.Đ.B
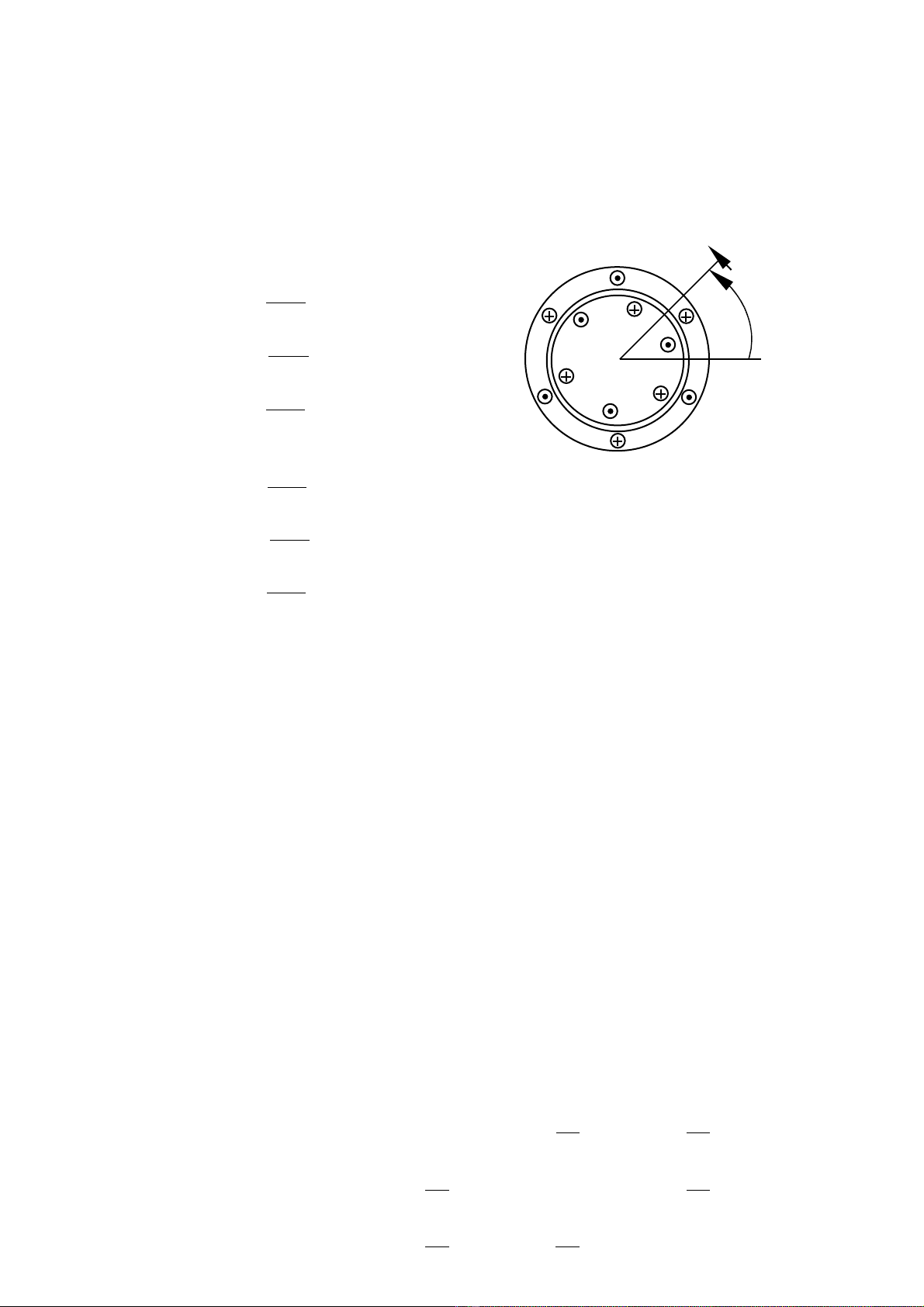
1. Phương trình điện áp: Ta xét một mô hình động cơ không đồng bộ như hình vẽ
bên.
Phương trình điện áp của stato là:
as
as as s
bs
bs bs s
cs
cs as s
d
u i r dt
d
u i r dt
d
u i r dt
λ
= +
λ
= +
λ
= +
(1)
Phương trình điện áp của roto là:
ar
ar ar s
br
br br r
cr
cr ar r
d
u i r dt
d
u i r dt
d
u i r dt
λ
= +
λ
= +
λ
= +
(2)
2. Phương trình từ thông: Dựa trên khái niệm ma trận, từ thông móc vòng của dây
quấn stato và roto theo hệ số tự cảm của dây quấn và dòng điện có thể viết dưới dạng
ngắn gọn là:
abc abc abc abc
s ss sr s
abc abc
abc abc
rs rr
r r
L L i
L L i
λ=
λ
(3)
Trong đó:
as ar as ar
abc abc abc abc
s bs r br s bs r br
cs cr cs cr
i i
[ ] [ ] [i ] i [i ] i
i i
λ λ
λ = λ λ = λ = =
λ λ
(4)
Các ma trận con của hệ số tự cảm có dạng:
s ss sm sm
abc
ss sm s ss sm
sm sm s ss
L L L L
[L ] = L L L L
L L L L
σ
σ
σ
+
+
+
(5)
r rr rm rm
abc
rr rm s rr rm
rm rm s rr
L L L L
[L ] L L L L
L L L L
σ
σ
σ
+
= +
+
(6)
r r r
T
abc abc
sr rs sr r r r
r r r
2 2
cos cos cos
3 3
2 2
L L L cos cos cos
3 3
2 2
cos cos cos
3 3
π π
θ θ + θ −
π π
= = θ − θ θ +
π π
θ + θ − θ
(7)
27
Trục pha a
as
-as
bs
-bs
cs
-cs ar
-ar
br
-brcr
-cr
θr
ωr

Trong đó
s
L
σ
là hệ số tự cảm ứng với từ trường tản của một pha của dây quấn stato,
r
L
σ
là hệ số tự cảm ứng với từ trường tản của một pha của dây quấn roto,
ss
L
là hệ số
tự cảm của một pha của dây quấn stato,
rr
L
là hệ số tự cảm của một pha của dây quấn
roto,
sm
L
là hệ số hỗ cảm giữa các pha của dây quấn stato,
rm
L
là hệ số hỗ cảm giữa
các pha của dây quấn roto và
sr
L
là giá trị biên độ của hệ số hỗ cảm giữa dây quấn
stato và dây quấn roto.
Ta có thể biểu diễn các điện kháng theo số vòng dây stato
s
W
, số vòng dây roto
r
W
và độ từ thẩm của khe hở không khí
δ
ρ
:
2
ss s
L W
δ
= ρ
2
rr r
L W
δ
= ρ
2
sm s
2
L W cos 3
δ
π
= ρ
2
rm r
2
L W cos 3
δ
π
= ρ
(8)
sr s r
L W W
δ
= ρ
Máy điện lí tưởng được mô tả bằng hệ 6 phương trình vi phân cấp 1, mỗi phương
trình cho một dây quấn. Các phương trình này liên kết với nhau qua hệ số hỗ cảm
giữa các dây quấn. Đặc biệt các số hạng liên kết dây quấn stato và roto là hàm của vị
trí roto. Như vậy khi roto quay, các số hạng này biến thiên theo thời gian. Các biến
đổi toán học giống như dq hay αβ có thể làm cho việc tính toán nghiệm quá độ của
mô hình đ.c.k.đ.b nêu trên trở nên dễ dàng bằng cách biến đổi các phương trình vi
phân có hệ số tự cảm và hỗ cảm biến đổi theo t thành các phương trình vi phân có hệ
số tự cảm và hỗ cảm hằng.
§2. MÔ HÌNH M.Đ.K.Đ.B TRONG HỆ qd0 TUỲ Ý
1. Khái niệm chung: M.đ.k.đ.b 3 pha lí tưởng có khe hở không khí đối xứng. Các hệ
qd0 thường được chọn trên cơ sở tương thích với các thành phần khác của mạng. Hai
hệ thường được chọn khi phân tích máy điện là hệ cố định và hệ quay đồng bộ. Mỗi
hệ có những ưu điểm riêng và thích hợp với những mục đích riêng. Trong hệ cố định,
các biến dq của máy điện có cùng một thứ nguyên như các biến thường được dùng
trong hệ thống cung cấp điện. Đây là lựa chọn thích hợp khi hệ thống cung cấp điện
lớn hay phức tạp. Trong hệ toạ độ quay đồng bộ, các biến dq là các biến xác lập trong
chế độ xác lập, một đòi hỏi tiên quyết khi rút ra mô hình tín hiệu nhỏ quanh điểm làm
việc đã chọn. Trước hết ta xây dựng các phương trình của m.đ.k.đ.b trong hệ toạ độ
tuỳ ý quay với tốc độ ω cùng chiều với roto.
Khi đó để có phương trình của máy điện
trong hệ toạ độ cố định ta chỉ cần cho ω = 0
và nếu cho ω = ωe thì ta có hệ phương trình
trong hệ toạ độ quay đồng bộ với roto.
Trước hết ta viết phương trình điện áp và
mômen theo các đại lượng pha. Quan hệ
giữa các đại lượng abc và qd0 tuỳ ý như
hình vẽ bên. Áp dụng phép biến đổi hệ toạ
độ qd0 tuỳ ý vào các phương trình này ta sẽ
có các phương trình qd0 tương ứng.
28
Trục q
Trục d
θ
θr
ω
ωr
as
bs
cs
ar
br
cr

Phương trình biến đổi từ hệ abc sang hệ qd0 là:
q a
d qd0 b
0 c
f f
f T (θ) f
f f
=
(9)
Trong đó f có thể là điện áp các pha, dòng điện hay từ thông của máy. Góc chuyển toạ
độ θ(t) giữa trục q của hệ toạ độ quay ở tốc độ ω và trục a của hệ toạ độ cố định có thể
biểu diễn bằng biểu thức:
t
0
θ(t) ω(t)dt θ(0)
= +
∫
độ điện (10)
Tương tự, góc θr(t) giữa trục của stato và roto của pha a khi roto quay với tốc độ ωr(t)
có thể biểu diễn bởi:
t
r r r
0
θ (t) ω (t)dt θ (0)
= +
∫
độ điện (11)
Các góc θ(0) và θr(0) là các giá trị đầu của các góc này tại thời điểm t = 0. Từ (14) của
chương trước ta có:
( )
qd0
2 2
cosθ cos θ cos θ
3 3
2 2 2
T sinθ sin θ sin θ
3 3 3
1 1 1
2 2 2
π π
− +
π π
θ = − +
(12)
và nghịch đảo của nó:
( )
1
qd0
cosθ sinθ 1
1
2 2 2
Tθ cos θ sin θ
3 3 3
1
2 2
cosθ sin θ
3 3
−
π π
= − −
π π
+ +
(13)
2. Phương trình điện áp qd0: Ta có thể biểu diễn điện áp của các dây quấn abc dưới
dạng ma trận:
abc abc abc abc
s s s s
[u ] p[ ] [r ][i ]
= λ +
(14)
Trong đó p là toán tử đạo hàm.
Áp dụng các phép biến đổi,
)](T[
0qd
θ
vào điện áp, từ thông móc vòng và dòng điện,
phương trình (14) có dạng:
1 1
qd0 qd0 qd0
abc
s qd0 qd0 s qd0 s qd0 s
u T (θ) p T (θ) T (θ) r T (θ) i
− −
= λ +
(15)
Số hạng đạo hàm theo t được viết là:
{ } { }
qd0 qd0 qd0
qd0 s qd0 s qd0 s
d d
p T (θ) T (θ) T (θ)
dt dt
λ = λ + λ =
29

1
qd0 qd0
s qd0 s
sinθ cosθ 0
2π 2π dθ
sinθ cos θ 0 T (θ) p
3 3 dt
2π 2π
sinθ cos θ 0
3 3
−
−
− − − λ + λ
− + +
(16)
Thay lại vào (15) ta có:
qd0 qd0 qd0 qd0 qd0
s s s s s
0 1 0
u 1 0 0 p r i
0 0 0
= ω − λ + λ +
(17)
Trong đó:
dθ
dt
ω =
qd0
s s
1 0 0
r [r ] 1 1 0
0 0 1
=
(18)
Tương tự, các đại lượng roto cũng phải được chuyển sang hệ toạ độ qd. Từ hình vẽ
trên ta có thể thấy rằng góc chuyển đổi đối với các đại lượng roto là (θ - θr). Áp dụng
phép biến đổi, [Tqd0(θ - θr)] vào các phương trình điện áp roto theo cùng một các như
đối với các phương trình điện áp stato ta có:
( )
qd0 qd0 qd0 qd0 qd0
r r r r r r
0 1 0
[u ]ω ω 1 0 0 [λ ] p[λ ] [r ][i ]
0 0 0
= − − + +
(19)
3. Quan hệ từ thông móc vòng qd0: Các từ thông móc vòng qd0 nhận được bằng cách
áp dụng [Tqd0(θ)] vào các từ thông móc vòng stato abc trong (3):
[ ]
(
)
qd0 abc abc abc abc
s qd0 ss s sr r
[ ] T (θ) [L ][i ] [L ][i ]
λ = +
(20)
Sử dụng biến đổi ngược thích hợp để thay thế các dòng điện stato và roto bằng các
thành phần dòng điện tương ứng qd0, phương trình (20) trở thành:
1 1
qd0
qd0 qd0
abc abc
s qd0 ss qd0 s qd0 sr qd0 r r
σs ss sr
qd0 qd0
s r
σs ss sr
σs
λ T (θ) L T (θ) i T (θ) L T (θ θ ) i
3 3
L L 0 0 L 0 0
2 2
3 3
i i
0 L L 0 0 L 0
2 2
0 0 L 0 0 0
− −
= + −
+
= +
+
(21)
Tương tự từ thông móc vòng của roto cho bởi:
1 1
qd0 qd0 qd0
abc abc
r qd0 r rs qd0 s qd0 r rr qd0 r r
srσr rr
qd0 qd0
s r
srσr rr
σr
[λ ] T (θ θ ) [L ] T (θ) [i ] T (θ-θ ) [L ] T (θ θ ) [i ]
3 3
L 0 0 L L 0 0
2 2
3 3
i i
0 L 0 0 L L 0
2 2
0 0 0 0 0 L
− −
= − + −
+
= +
+
(22)
Quan hệ từ thông stato và roto trong (21) và (22) có thể viết gọn lại dưới dạng:
30
qsσs m m qs
dsσs m m ds
0sσs 0s
qr mσr m qr
dr mσr m dr
0rσr 0r
λ L L 0 0 L 0 0 i
λ 0 L L 0 0 L 0 i
λ 0 0 L 0 0 0 i
λ L 0 0 L L 0 0 i
λ 0 L 0 0 L L 0 i
λ 0 0 0 0 0 L i
+
+
=
′ ′ ′
+
′ ′ ′
+
′ ′ ′
(23)
Trong đó các đại lượng roto ban đầu được quy đổi về các đại lượng stato theo quan
hệ sau:
s s
qr qr dr dr
r r
W W
λ λ λ λ
W W
′ ′
= =
(24)
dr
r
s
dr
qr
r
s
qr
i
W
W
ii
W
W
i
=
′
=
′
(25)
r
2
r
s
r
L
W
W
L
σσ
=
′
(26)
Trong đó Lm là hệ số hỗ cảm từ hoá phía stato và bằng:
rr
r
s
sr
r
s
ssm
L
W
W
2
3
L
W
W
2
3
L
2
3
L
===
(27)
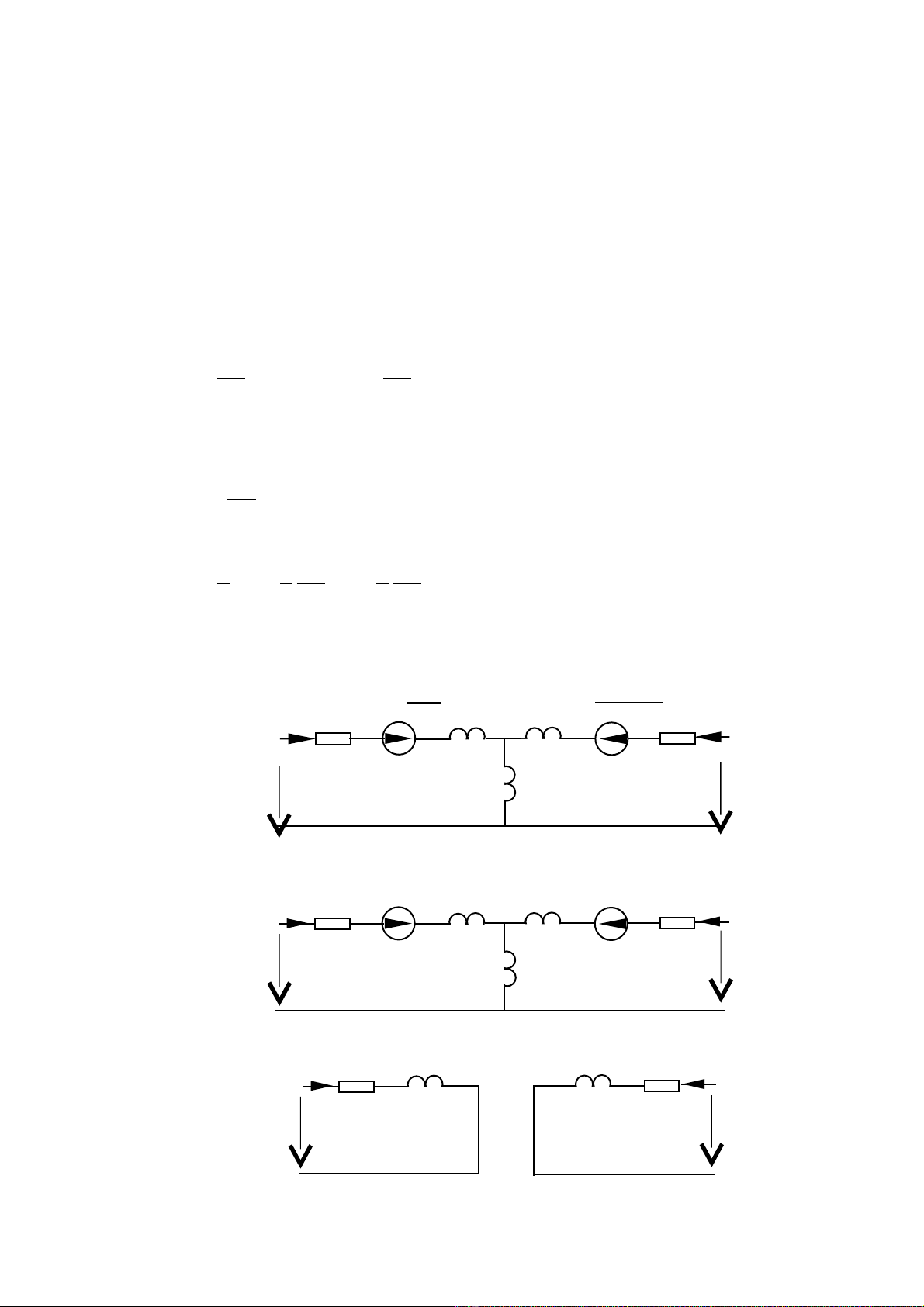
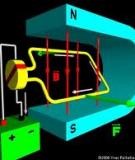
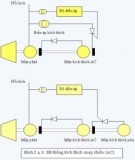
Thay (23) vào (17) và (19) rồi nhóm các số hạng q, d, 0 và θ trong các phương trình
điện áp ta có mạch thay thế tương đương của m.đ.k.đ.b trong hệ qd tuỳ ý như sau:
3. Phương trình mô men: Tổng công suất vào tức thời của 6 dây quấn stato và roto
cho bởi:
31
Trục 0
r
x
σ
′
r
r
′
r0
i
′
dr
u
′
i0s
rs
s
x
σ
u0s
xm
qr
E
′
iqs
rs
ds
b
ω
Ψω
s
x
σ
r
x
σ
′
r
dr
b
ω − ω
′
Ψω
r
r
′
qr
i
′
qr
u
′
Trục q
Eqs
uqs
uds
ids
rs
s
x
σ
r
x
σ
′
r
r
′
dr
i
′
xm
dr
u
′
Trục d
Eds
dr
E
′





![Sổ giáo án thực hành Máy DVD Trần Duy Khánh [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2017/20170313/kakavt20/135x160/8341489413963.jpg)







![Chương trình đào tạo cơ bản Năng lượng điện mặt trời mái nhà [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260126/cristianoronaldo02/135x160/21211769418986.jpg)

![Chương trình đào tạo cơ bản Năng lượng gió [Tối ưu SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260126/cristianoronaldo02/135x160/53881769418987.jpg)








