TR NG Đ I H C K THU T CÔNG NGHI PƯỜ Ạ Ọ Ỹ Ậ Ệ
KHOA ĐI N TỆ Ử
B môn: Đi n t Vi n Thôngộ ệ ử ễ
NGÂN HÀNG CÂU H I THI K T THÚC H C PH NỎ Ế Ọ Ầ
H C PH N: X LÝ TÍN HI U SỌ Ầ Ử Ệ Ố
(3 TÍN CH )Ỉ
DÙNG CHO ĐÀO T O B C Đ I H C THEO H C CH TÍN CHẠ Ậ Ạ Ọ Ọ Ế Ỉ
CHUYÊN NGÀNH ĐI N T VI N THÔNGỆ Ử Ễ
THÁI NGUYÊN – 8/2007
TR NG Đ I H CƯỜ Ạ Ọ
K THU T CÔNG NGHI PỸ Ậ Ệ
Khoa Đi n tệ ử
B môn: Đi n t Vi n Thôngộ ệ ử ễ
C NG HOÀ XÃ H I CH NGHĨA VI T NAMỘ Ộ Ủ Ệ
Đ c l p – T do – H nh phúcộ ậ ự ạ
Thái Nguyên, ngày 12 tháng 8 năm 2007
NGÂN HÀNG CÂU H I THIỎ
X LÝ TÍN HI U SỬ Ệ Ố
S d ng cho h đ i h c theo các chuyên ngành:ử ụ ệ ạ ọ
1. N I DUNG ĐÁNH GIÁ THI K T THÚC H C PH NỘ Ế Ọ Ầ
Yêu c u sinh viên n m đ c các ki n th c trong vi c kh o sát tín hi u cũngầ ắ ượ ế ứ ệ ả ệ
nh h th ng x lý tín hi u s trên mi n Z, mi n t n s liên t c ư ệ ố ử ệ ố ề ề ầ ố ụ
ω
và thi t k các bế ế ộ
l c s .ọ ố
2. PH NG PHÁP ĐÁNH GIÁƯƠ
Thi k t thúc h c ph n là thi vi t v i th i l ng 90 phút, ch m đi m theo thangế ọ ầ ế ớ ờ ượ ấ ể
đi m 10.ể
3. NGUYÊN T C T H P Đ THIẮ Ổ Ợ Ề
-M i đ thi có 3 câu h i.ỗ ề ỏ
-M i đ thi đ c t h p t 3 câu h i trong các ph n 4.1; 4.2; 4.3.ỗ ề ượ ổ ợ ừ ỏ ầ
4. NGÂN HÀNG CÂU H IỎ
4.1. CÂU H I LO I 1 (3 ĐI M)Ỏ Ạ Ể
1. Đ nh nghĩa bi n đ i Z và bi n đ i Z ng c? Các tính ch t c a bi n đ i Z?ị ế ổ ế ổ ượ ấ ủ ế ổ
2. Đ nh nghĩa bi n đ i Fourie và bi n đ i Fourie ng c? Các tính ch t c aị ế ổ ế ổ ượ ấ ủ
bi n đ i Fourie?ế ổ
3. Đ nh nghĩa bi n đ i Z ?bi n đ i Fourie ? M i quan h gi a chúng?ị ế ổ ế ổ ố ệ ữ
4. Đ nh nghĩa bi n đ i Z m t phía? Bi n đ i Z hai phía? So sánh?ị ế ổ ộ ế ổ
5. Tìm đ c tính xung h (n) c a h x lý s có s đ hình kh i hìnhặ ủ ệ ử ố ơ ồ ố ở
sau:
2
-rect (n-1)
y(n)
rect 2(n) 2δ(n-1)
2
rect 3(n-1)
2δ(n-2)
x(n)
y(n)
rect
3
(n-1)
x(n)
2n
6. Hãy xây d ng s đ c u trúc d ng chu n t c 1 và d ng chu n t c 2ự ơ ồ ấ ạ ẩ ắ ạ ẩ ắ
c a h x lý s có ph ng trình sai phân sau : ủ ệ ử ố ươ
4y (n) – 2y (n-2) = 2x (n) + x (n-1)
7. Hãy xây d ng s đ c u trúc c a h x lý s có s đ kh i theo đ cự ơ ồ ấ ủ ệ ử ố ơ ồ ố ặ
tính xung h(n) trên hình sau:
8. Tìm hàm t ng quan c a dãy x(n) = aươ ủ nrect(n)3 v i các dãy s sau : ớ ố
1. y1(n) = u(n) 3. y4(n) = rect(n)N
2. y2(n) = u(-n) 4. y5(n) =
δ
(n)
9. Hãy xác đ nh hàm t t ng quan rị ự ươ x (m) c a các dãy sau : ủ
1. x1(n) =
δ
(n) 3. x4(n) = rect(n)N
2. x2(n) =
δ
(-n) 4. x5(n) = rect(n-k)N
10. Tính hàm t ng quan ươ
)(m
rxy
c a dãy ủ
( ) . ( )
n
x n a u n=
v i các dãy :ớ
1.
1
( ) ( )n u n
y= =
3.
( ) ( )
4
y n rect n N
=
2.
11. Hãy xác đ nh hàm t t ng quan ị ự ươ
)(m
rx
c a các dãy sau:ủ
1. x1(n) = u(n) 3.
3
( ) ( )
N
x n rect n=
2. x2(n) = anu(n) 4.
4
( ) ( )
n
N
x n a rect n=
4.2. CÂU H I LO I 2 (3 ĐI M)Ỏ Ạ Ể
1. Hãy xác đ nh tính n đ nh c a các h x lý s TTBBNQ sau:ị ổ ị ủ ệ ử ố
a.
1 2
11 2
3 2
( ) (2 5 3 )
z z
H z z z
− −
− −
− +
=+ −
b.
1
6 2
( ) (3 2 10 4)
z
H z z z
+
=+ +
2. Hãy xác đ nh tính n đ nh c a các h x lý s TTBBNQ sau:ị ổ ị ủ ệ ử ố
a.
3
11 2 3
1
( ) (6 8 5 2 )
z
H z z z z
−
− − −
−
=− − −
b.
2
24 3 2
5 3
( ) (9 12 1.75 3 1)
z z
H z z z z z
+ −
=− + + −
3
3. Tìm ph n ng y(n) và xét tính n đ nh c a h x lý s có ph ngả ứ ổ ị ủ ệ ử ố ươ
trình sai phân:
( ) 3 ( -1) -1.75 ( - 2) - ( ) 3 ( - 2)y n y n y n x n x n= +
, v i tácớ
đ ng ộx(n) = 3nu(n-1), và đi u ki n ban đ u y(-2) = 1, y(-1) = 2.ề ệ ầ
4. V i ớ
1a<
, hãy xác đ nh s t n t i và tìm bi n đ i Fourier c a cácị ự ồ ạ ế ổ ủ
dãy sau:
a. x1(n) = anu(n) b. x5(n) = u(n).sin(
0
ω
.n)
5. V i ớ
1a<
, hãy xác đ nh s t n t i và tìm bi n đ i Fourier c a cácị ự ồ ạ ế ổ ủ
dãy sau:
a. x2(n) = a-nu(n) b. x6(n) = anu(n)sin(
0
ω
.n)
6. V i ớ
1a<
, hãy xác đ nh s t n t i và tìm bi n đ i Fourier c a cácị ự ồ ạ ế ổ ủ
dãy sau:
a. x3(n) = anu(-n) a. x7(n) = u(n).cos(
0
ω
.n)
7. V i ớ
1a<
, hãy xác đ nh s t n t i và tìm bi n đ i Fourier c a cácị ự ồ ạ ế ổ ủ
dãy sau:
a. x4(n) = a-nu(-n) b. x8(n) = anu(n)cos(
0
ω
.n)
8. Xác đ nh các hàm ph n th c và ph n o, modun và Acgumen, đ l nị ầ ự ầ ả ộ ớ
và pha c a các hàm t n s sau:ủ ầ ố
a.
0,3
1
( ) cos(3 ).
j j
X e e
ω ω
ω
−
=
b.
3
( ) 1 0,25.
j
j
j
e
X e e
ω
ω
ω
−
−
=−
9. Xác đ nh các hàm ph n th c và ph n o, modun và Acgumen, đ l nị ầ ự ầ ả ộ ớ
và pha c a các hàm t n s sau:ủ ầ ố
a.
( )
2
( ) 2 .
j j
X e Sin e
ω ω
ω
−
=
b.
( )
( )
4
3.
j j
X e e
ω α ω
− +
=
10. Cho dãy
1 Khi n [-N,N]
( ) 0 Khi n [-N,N]
x n
=
Xác đ nh X(ị
ω
j
e
), A(
ω
), B(
ω
),
ω
j
eX (
,
( )
ϕ ω
, A(
ω
j
e
),
( )
θ ω
11.Tìm bi n đ i Fourier ng c c a các hàm t n s sau:ế ổ ượ ủ ầ ố
a.
b.
X( ) = cos2
j
e
ω
ω
12.Tìm bi n đ i Fourier ng c c a các hàm t n s sau:ế ổ ượ ủ ầ ố
4
a.
0,5
( ) sin(2 )
j j
X e e
ω ω
−
=
b.
0,5
( ) cos(2 ).
j j
X e e
ω ω
ω
−
=
13. H x lý s có đ c tính xung ệ ử ố ặ
2
( ) ( -1)h n rect n=
, hãy tìm ph n ngả ứ
y(n), hàm ph ổ
( )
j
Y e
ω
và các đ c tr ng ph c a y(n), khi tác đ ng vàoặ ư ổ ủ ộ
h là ệ
-
( ) 3 ( -1)
n
x n u n=
14. H x lý s có ph n ng ệ ử ố ả ứ
-
2
( ) 2.2 ( - 2) - 0,5 ( -1)
n
y n u n rect n=
và tác đ ngộ
-
( ) 2 ( -1)
n
x n u n=
. Hãy xác đ nh hàm truy n đ t ph c ị ề ạ ứ
j
H(e )
ω
, đ c tínhặ
xung h(n) và các đ c tính t n s c a h .ặ ầ ố ủ ệ
15. Tìm
j
H(e )
ω
,
)(
ω
j
eH
và
)(
ωϕ
c a h x lý s có ph ng trình saiủ ệ ử ố ươ
phân
1 1 1
( ) ( ) ( -1) ( - 2) ( -3) ( - 4)
2 6 24
y n x n x n x n x n x n= + + + +
16. Tìm
j
H(e )
ω
,
)(
ω
j
eH
và
)(
ωϕ
c a h x lý s có ph ng trình saiủ ệ ử ố ươ
phân
( ) ( ) ( - )y n x n x n N= +
, v i N là h ngớ ằ
số
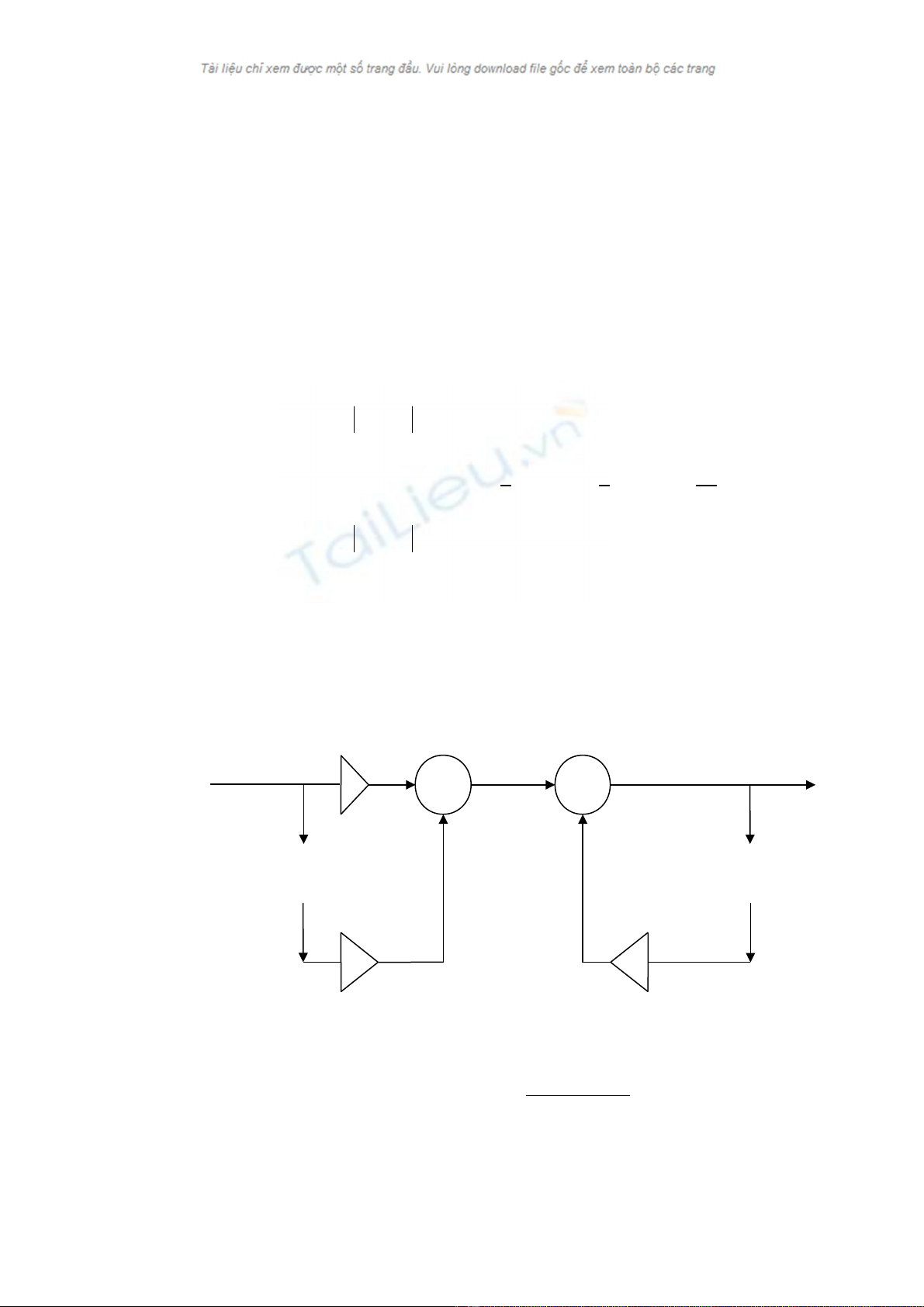
17.Tính đ c tính xung h(n) c a h x lý s TTBBNQ có s đ c u trúcặ ủ ệ ử ố ơ ồ ấ
trên hình sau, xét tính n đ nh c a hổ ị ủ ệ
18. Hãy xây d ng s đ c u trúc c a h x lý s có hàm h th ng là:ự ơ ồ ấ ủ ệ ử ố ệ ố
19.
2
3
( ) .(2 3)
H z z z z
=+ −
20. Cho h x lý s TTBBNQ có s đ c u trúc trên hình d i đây, tìmệ ử ố ơ ồ ấ ướ
ph n ng y(n) c a h khi tác đ ng ả ứ ủ ệ ộ
-
( ) 2 ( )sin(5. )
n
x n u n n=
5
+ +
Z
1
−
Z
1
−
X(z)
2
0,5
3
Y(z