CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025 Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Chuyên đề này liên quan kiến thức toán 11. Gồm có 2 nội dung
Nội dung 1. Phương trình lượng giác
Nội dung 2. Phương trình – bất phương mũ – logarit
Chuyên đề này được bên mình biên soạn dựa theo định hướng ôn thi 2025
PHẦN A. LÝ THUYẾT
I. PHƯƠNG TRÌNH LƯỢNG GIÁC
1. Phương trình lượng giác cơ bản
a) Phương trinh
sin x m
(1)
- Với
| | 1m
, phương trình (1) vô nghiệm.
- Với
| | 1m
, gọi
là số thực thuộc đoạn
;
2 2
sao cho
sin x m
.
Khi đó, ta có:
2
sin sin sin ( )
2
x k
x m x k
x k
.
Chú ý
- Ta có một số trường hợp đặc biệt sau của phương trình
sin x m
:
-
sin 1 2 ( )
2
x x k k
;
-
sin 1 2 ( )
2
x x k k
;
-
sin 0 ( )x x k k
.
- Nếu
x
là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác
x
sao cho
sin sinx a
như sau:
360
sin sin ( ).
180 360
x a k
x a k
x a k
b) Phương trình
cos x m
(2)
- Với
| | 1m
, phương trình (2) vô nghiệm.
- Với
| | 1m
, gọi
là số thực thuộc đoạn
[0; ]
sao cho
cos m
.
Khi đó, ta có:
2
cos cos cos ( )
2
x k
x m x k
x k
.
Chú ý
- Ta có một số trường hợp đặc biệt sau của phương trình
cos x m
:
- cos 1 2 ( );
- cos 1 2 ( ).
- cos 0 ( ).
2
x x k k
x x k k
x x k k
- Nếu
x
là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác
x
sao cho
cos cosx a
như sau:
360
cos cos ( ).
360
x a k
x a k
x a k
c) Phương trình
tan x m
Gọi
là số thực thuộc khoảng
;
2 2
sao cho
tan x m
. Khi đó, ta có:
CHUYÊN ĐỀ 12. PHƯƠNG TRÌNH - BẤT PHƯƠNG TRÌNH
• Fanpage: Nguyễn Bảo Vương - https://www.nbv.edu.vn/
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
tan tan tan ( ).
x m x x k k
Chú ý: Nếu
x
là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác
x
sao cho
tan tanx a
như sau:
tan tan 180 ( ).
x a x a k k
d) Phương trình
cot x m
Gọi
là số thực thuộc đoạn
sao cho
cot x m
. Khi đó, ta có:
cot cot cot ( ).
x m x x k k
Chú ý: Nếu
x
là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác
x
sao cho
cot cotx a
như sau:
cot cot 180 ( ).
x x k k
2. Phương trình lượng giác đưa về dạng cơ bản
-
( ) ( ) 2
sin ( ) sin ( ) ( )
( ) ( ) 2
f x g x k
f x g x k
f x g x k
.
( ) ( ) 2
cos ( ) cos ( ) ( )
( ) ( ) 2
f x g x k
f x g x k
f x g x k
- Với phương trình có dạng:
2 2 2 2 2 2
sin ( ) sin ( ),cos ( ) cos ( ),sin ( ) cos ( ),u x v x u x v x u x v x
ta có thể dùng công thức hạ bậc
để đưa về phương trình dạng
cos ( ) cos ( )f x g x
.
- Với một số phương trình lượng giác, ta có thể dùng các công thức lượng giác và các biến đổi
để đưa về phương trình dạng tích
( ) ( ) 0
A x B x
.
II. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LÔGARIT
1. Phương trình mũ
Với
0, 1
a a
thì:
-
( )
( ) log
f x
a
a b f x b
với
0
b
;
-
( ) ( )
( ) ( )
f x g x
a a f x g x
.
2. Phương trình lôgarit
Với
0, 1
a a
thì:
-
log ( ) ( )
b
a
f x b f x a
.
-
( ) ( )
log ( ) log ( )
( ) 0 ( ) 0.
a a
f x g x
f x g x f x g x
3. Bất phương trình mũ
Với
0, 1
a a
thì:
a) Xét bất phương trình:
( )f x
a b
.
- Nếu
0
b
, tập nghiệm của bất phương trình là tập xác định của
( )f x
;
- Nếu
0, 1
b a
thì bất phương trình đưa về:
( ) log
a
f x b
;
- Nếu
0,0 1b a
thì bất phương trình đưa về:
( ) log
a
f x b
.
b) Xét bất phương trình:
( ) ( )f x g x
a a
.
- Nếu
1
a
thì bất phương trình đưa về:
( ) ( )f x g x
;
- Nếu
0 1a
thì bất phương trình đưa về:
( ) ( )f x g x
.
Các bất phương trình mũ khác cùng loại được giải tương tự.
4. Bất phương trình lôgarit
Với
0, 1
a a
thì:
a) Xét bất phương trình:
log ( )
a
f x b
.
- Nếu
1
a
thì bất phương trình đưa về:
( )
b
f x a
;
- Nếu
0 1a
thì bất phương trình đưa về:
0 ( )
b
f x a
.
b) Xét bất phương trình:
log ( ) log ( )
a a
f x g x
.
Điện thoại: 0946798489 CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
- Nếu
1
a
thì bất phương trình đưa về:
( ) ( ) 0
f x g x
;
- Nếu
0 1a
thì bất phương trình đưa về:
0 ( ) ( )f x g x
.
Các bất phương trình lôgarit khác cùng loại được giải tương tự.
PHẦN B. BÀI TẬP TỰ LUẬN
DẠNG 1. PHƯƠNG TRÌNH LƯỢNG GIÁC
Câu 1. Giải các phương trình lượng giác sau:
a)
6sin 2 3 0
x
.
b)
sin sin
5 3
x
.
c)
sin 4 cos 180 3 0
x x
.
Câu 2. Giải các phương trình lượng giác:
a)
cos6 1
x
.
c)
1
2cos 2 8cos 7
cos
x x
x
.
b)
cos cos 6
x
.
Câu 3. Giải các phương trình lượng giác:
a)
tan(2 1) tan 3
x
.
b)
tan 2 25 1
x
.
c)
2
tan cot
sin
x x
x
Câu 4. Giải các phương trình lượng giác sau:
a)
2
3 sin sin cos 0
x x x
.
b)
sin 2 2 sin( ) cos(2 )
x x x
.
c) 2 2
1
4cos sin 3sin 3
2 2 2
x x
x
.
Câu 5. Giải các phương trình lượng giác sau:
a)
cos cox5 cos2 cos4x x x x
.
b)
2cos cos2 1 cos2 cos3x x x x
.
Câu 6. Giải các phương trình lượng giác sau:
a)
tan 2 30 tan 20 0
x
.
b)
3 3
cos 2 sin 2 sin 2 cos 2x x x x
.
Câu 7. Giải các phương trình lượng giác sau:
a)
5tan 2cot 3 0
x x
.
b)
2
cot 3 tan
5
x
.
c)
1 2(cos sin )
tan cot 2 cot 1
x x
x x x
.
Câu 8. Tìm
m
để các phương trình lượng giác sau có nghiệm:
a)
2sin3 1
x m
.
b)
2 2
3sin sin 2 cos 0
x x m x
.
c)
tan 2
m x m
.
Câu 9. Giải các phương trình lượng giác:
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
a)
cot 20 3
4
x
.
b)
cot 3 cot
3
x
c)
cot sin 1 tan tan 4
4
x
x x x
.
Câu 10. Tìm nghiệm phương trình sau trên các khoảng đã cho:
a) 1
sin 2 ,0
2
x x
.
b)
tan 2 15 1, 180 90
x x
.
c)
1
cot 3 , 0
2
3
x x
.
DẠNG 2. PHƯƠNG TRÌNH – BẤT PHƯƠNG TRÌNH MŨ & LOGARIT
Câu 11. Giải phương trình sau:
a)
2
5 1
1
3
3
x x
(1)
b)
3 4 1
2 ( 2)
x x
(2).
Câu 12. Giải phương trình sau:
a)
5
log (2 3 ) 2
x
(1)
b)
2 2
log (3 1) log ( 2) 1
x x
(2)
Câu 13. Giải các phương trình sau:
a)
1
3 27
x
;
b) 2
2
4 16
x
;
c)
1 3 2
8 4
x x
d)
2
3 5 75
x x
.
Câu 14. Giải các phương trình sau:
a)
2
log ( 1) 3
x
.
b)
2
log 9 1
x x
;
c)
2 2
log log ( 1) 1
x x
;
d)
ln( 1) ln( 3) ln( 7)
x x x
;
Câu 15. Giải các bất phương trình sau:
a)
2
5 3
1
8
2
x x
b) 2
1
5 25
x x x
;
c)
1 2 1
2 2 3 3
x x x x
.
Câu 16. Giải các bất phương trình sau:
a)
2
3
log 3 11 4
x x
;
b)
3 3
log (3 1) log (2 7)
x x
;
c)
5 5
log (1 2 ) 1 log ( 1)
x x
.
Câu 17. Giải bất phương trình sau:
a)
1 2
1
49
7
x
(1)
Điện thoại: 0946798489 CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
b)
2
1 2
9 3
x x
(2)
Câu 18. Giải bất phương trình sau:
a)
1
3
log ( 6) 3
x
(1)
b)
2
log( 5) log 4 5x x x
(2)
DẠNG 3. ỨNG DỤNG THỰC TẾ
Câu 19. Một quả đạn pháo được bắn ra khỏi nòng pháo với vận tốc ban đầu có độ lớn
0
v
không đổi.
Tìm góc bắn
để quả đạn pháo bay xa nhất, bở qua sức cản của không khí và coi quả đạn pháo được
bắn ra từ mặt đất.
Câu 20. Trong Hình 9, khi được kéo ra khỏi vị trí cân bằng ờ điểm
O
và buông tay, lực đàn hồi của lò
xo khiến vật
A
gắn ở đầu của lò xo dao động quanh
O
. Toạ độ
( )s cm
của
A
trên trục
Ox
vào thời điểm
t
(giây) sau khi buông tay được xác định bởi công thức
10sin 10 2
s t
. Vào các thời điểm nào thì
5 3 s cm
?
(Theo https://ww.britannica.com/science/simple-harmonic-motion)
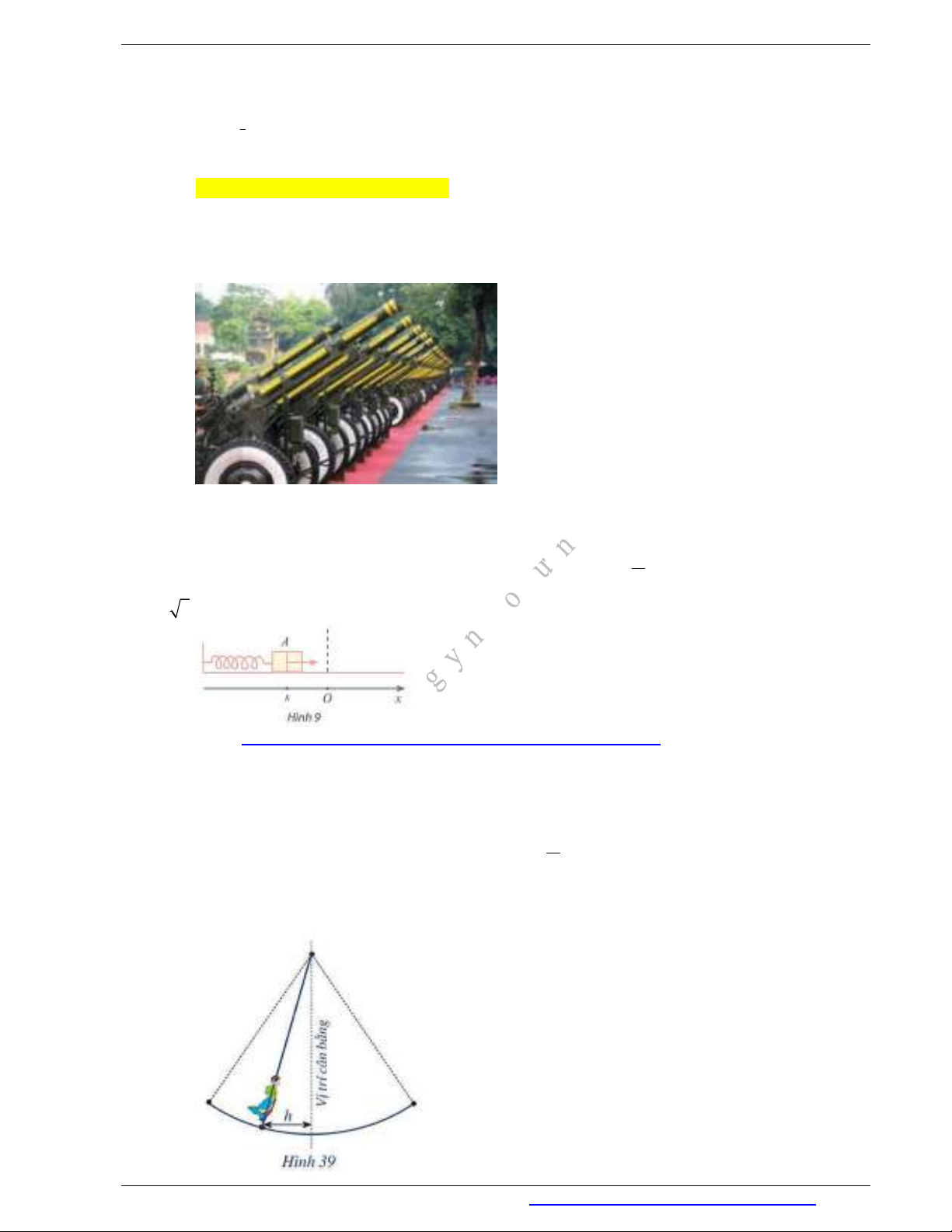
Câu 21. Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người
chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 39). Nghiên cứu trò
chơi này, người ta thấy khoảng cách
( )h m
từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua
thời gian t (s) (với
0t
) bởi hệ thức
| |h d
với
3cos (2 1)
3
d t
, trong đó ta quy ước
0d
khi vị
trí cân bằng ở phía sau lưng người chơi đu và
0d
trong trường hợp ngược lại (Nguồn: Đại số và Giải
tích 11 Nâng cao, NXBGD Việt Nam, 2020). Vào thời gian t nào thì khoảng cách
h
là
3 ;0 m m
?