CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025 Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN A. LÝ THUYẾT VÀ VÍ DỤ
I. PHƯƠNG TRÌNH ĐƯỜNG THẲNG
1. Vectơ chỉ phương của đường thẳng
Cho đường thẳng
và vectơ
u
khác
0
. Vectơ
u
được gọi là vectơ chỉ phương của đường
thẳng
nếu giá của
u
song song hoặc trùng với
.
Nhận xét: Nếu
u
là vectơ chỉ phương của một đường thẳng thì
( 0)ku k
cũng là vectơ chỉ
phương của đường thẳng đó.
Ví dụ 1: Trong Hình, các vectơ
,AB CD
và
A B
có là vectơ chỉ phương của đường thẳng
AB
hay
không? Vì sao?
Giải
Do vectơ
AB
khác
0
và có giá là đường thẳng
AB
nên vectơ
AB
là vectơ chỉ phương của
đường thẳng
AB
.
2. Phương trình tham số của đường thẳng
Trong trường hợp tổng quát, ta có:
- Trong không gian với hệ tọa độ
Oxyz
, nếu
là đường thẳng đi qua
0 0 0 0
; ;M x y z
và có
vectơ chỉ phương
( ; ; )u a b c
thì
có phương trình dạng
0
0
0
x x at
y y bt
z z ct
(t là tham số)
- Ngược lại, mỗi hệ phương trình
0
0
0
x x at
y y bt
z z ct
, trong đó
, ,abc
không đồng thời bằng 0 và
t
là
tham số, xác định đường thẳng
đi qua
0 0 0 0
; ;M x y z
và có một vectơ chỉ phương là
( ; ; )u a b c
.
Hệ phương trình
0
0
0
x x at
y y bt
z z ct
, trong đó
, ,abc
không đồng thời bằng
0,t
là tham số, được gọi
là phương trình tham số của đường thẳng
đi qua
0 0 0 0
; ;M x y z
và có vectơ chỉ phương
( ; ; )u a b c
.
Trong các ví dụ, bài tập sau đây, nếu không chú ý gì thêm thì ta hiểu là xét trong không gian
với hệ toạ độ
Oxyz
.
Ví dụ 2
a) Viết phương trình tham số của đường thẳng
đi qua điểm
(2; 1;4)A
và có vectơ chỉ
phương
(3;4; 5)u
.
CHUYÊN ĐỀ 20. PHƯƠNG TRÌNH MẶT PHẲNG
• Fanpage: Nguyễn Bảo Vương - https://www.nbv.edu.vn/
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
b) Cho đường thẳng
có phương trình tham số là:
1 2
5 7
9
x t
y t
z t
(
t
là tham số).
Chỉ ra toạ độ một vectơ chỉ phương của
và một điểm thuộc đường thẳng
.
Giải
a) Phương trình tham số của đường thẳng
là:
2 3
4 7
6 8
x t
y t
z t
(t là tham số)
b) Toạ độ của một vectơ chỉ phương của
là
u
Ứng với
0t
ta có:
1 2 0 1
5 7 0 5
9 0 0.
x
y
z
Suy ra điểm
( 1;5;0)
B
thuộc đường thẳng
.
3. Phương trình chính tắc của đường thẳng
Trong trường hợp tổng quát, ta có:
- Trong không gian với hệ toạ độ
Oxyz
, nếu
là đường thẳng đi qua điểm
0 0 0 0
; ;M x y z
và
có vectơ chỉ phương
( ; ; )u a b c
(với
0)
abc
thì
có phương trình dạng:
0 0 0
.
x x y y z z
a b c
- Ngược lại, với
0
abc
, mỗi hệ phương trình
0 0 0
x x y y z z
a b c
xác định đường thẳng
đi qua
0 0 0 0
; ;M x y z
và có một vectơ chỉ phương là
( ; ; )u a b c
.
Nếu
0
abc
thì hệ phương trình
0 0 0
x x y y z z
a b c
được gọi là phương trình chính tắc
của đường thẳng
đi qua
0 0 0 0
; ;M x y z
và có vectơ chỉ phương
( ; ; )u a b c
.
Ví dụ 2: Viết phương trình chính tắc của đường thẳng
đi qua điểm
(1;3;6)
A
và có vectơ chỉ phương
(9;2;13)
u
.
Giải
Phương trình chính tắc của đường thẳng
đi qua điểm
(1;3;6)
A
và có vectơ chỉ phương
(9;2;13)
u
là:
1 3 6 .
9 2 13
x y z
4. Lập phương trình đường thẳng đi qua hai điểm cho trước
Đường thẳng
đi qua hai điểm
0 0 0 1 1 1
; ; , ; ;A x y z B x y z
có:
- Phương trình tham số là:
0 1 0
0 1 0
0 1 0
x x x x t
y y y y t
z z z z t
(
t
là tham số).
- Phương trình chính tắc là:
0 0 0
1 0 1 0 1 0
x x y y z z
x x y y z z
(với
0 1 0 1 0 1
, ,
x x y y z z
).
Ví dụ 3: Lập phương trình chính tắc và phương trình tham số của đường thẳng
AB
biết
(4;1;2)
A
và
(5;8;6)
B
.
Giải
- Phương trình chính tắc của đường thẳng
AB
là:
4 1 2 4 1 2 .
5 4 8 1 6 2 1 7 4
x y z x y z
Điện thoại: 0946798489 CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
- Phương trình tham số của đường thẳng
AB
là:
4
1 7
2 4
x t
y t
z t
(t là tham số)
II. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG
Trước hết, ta có định nghĩa sau: Trong không gian, hai vectơ được gọi là cùng phuơng nếu các
giá của chúng cùng song song với một đường thẳng, ba vectơ được gọi là đồng phẳng nếu các
giá của chúng cùng song song với một mặt phẳng.
Người ta cũng chứng minh được những điều kiện sau.
Trong không gian
Oxyz
, cho ba vectơ
1 1 1 1 2 2 2 2 3 3 3 3
; ; ; ; ; ; ; ; .u a b c u a b c u a b c
- Hai vectơ
1 2
,u u
là cùng phương khi và chỉ khi
1 2
, 0
u u
.
- Ba vectơ
1 2 3
, ,u u u
là đồng phẳng khi và chỉ khi
1 2 3
, . 0
u u u
.
Ta có định lí sau:
Trong không gian với hệ toạ độ
Oxyz
, cho hai đường thẳng phân biệt
1 2
,
lần lượt đi qua các
điểm
1 2
,M M
và tương ứng có
1 2
,u u
là hai vectơ chỉ phương. Khi đó, ta có:
1 2
1 2
1 2
1 1 2 1 1 2
1 2 1 2
1 2
1 2 1 2 1 2 1 2
, 0
, cïng ph¬ng
/ / , kh«ng cïng ph¬ng
, 0.
, kh«ng cïng ph¬ng , 0
c¾t , , ®ång ph¼ng
, 0
u u
u u
u M M u M M
u u u u
u u M M u u M M
.
1 2 1 2 1 2
và chéo nhau , 0.
u u M M
Chú ý: Trong một số trường hợp, để xét vị trí tương đối của hai đường thẳng, ta có thể giải hệ
phương trình được lập từ những phương trình xác định hai đường thẳng đó, sau đó xét cặp
vectở chỉ phương của hai đường thẳng đó có cùng phương hay không (nếu cẩn thiết).
Ví dụ 4: Xác định vị trí tương đối của hai đường thẳng
1 2
,
trong mỗi trường hợp sau:
a)
1 2
1 1 2 2
1 2
1 5 2 10
: 2 , : 4 2
3 2 1 4
x t x t
y t y t
z t z t
;
b)
1 2
2 3 4 2 1 2
: , :
3 2 1 2 1 3
x y z x y z
;
c)
1 2
6 3
3 1 2
: , : 8 2
1 1 2
1 .
x t
x y z
y t
z t
Giải
a) Đường thẳng
1
đi qua điểm
1
(1;2;3)
M
và có
1
(5; 1;2)
u
là vectơ chỉ phương. Đường
thẳng
2
đi qua điểm
2
(2;4;1)
M
và có
2
(10; 2;4)
u
là vectơ chỉ phương.
Ta có:
1 2
2 (10; 2;4)
u u
, suy ra
1 2
,u u
cùng phương;
1 2 1 1 2
1 2
(1;2; 2) và nên , không cùng phu'o'ng.
5 1
M M u M M
Vậy
1 2
/ /
.
b) Đường thẳng
1
đi qua điểm
1
(2;3; 4)
M
và có
1
(3;2;1)
u
là vectơ chỉ phương. Đường
thẳng
2
đi qua điểm
2
( 2;1;2)
M
và có
2
(2;1; 3)
u
là vectơ chỉ phương. Ta có:
2 1
3 2
, suy
ra
1 2
,u u
không cùng phương;
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
1 2 1 2
2 1 1 3 3 2
( 4; 2;6), , ; ; ( 7;11; 1).
1 3 3 2 2 1
M M u u
Do
1 2 1 2
, ( 7) ( 4) 11 ( 2) ( 1) 6 0
u u M M
nên
1 2 1 2
, ,
u u M M

đồng phẳng.
Vậy
1
cắt
2
.
c) Đường thẳng
1
đi qua điểm
1
( 3;1;2)
M
và có
1
(1; 1;2)
u
là vectơ chỉ phương. Đường
thẳng
2
đi qua điểm
2
(6;8; 1)
M
và có
2
(3;2; 1)
u
là vectơ chỉ phương. Ta có:
1 2 1 2
1 2 2 1 1 1
(9;7; 3), , ; ; ( 3;7;5).
2 1 1 3 3 2
M M u u
Do
1 2 1 2
, ( 3) 9 7 7 5 ( 3) 7 0
u u M M
nên
1 2 1 2
, ,
u u M M

không đồng phẳng.
Vậy
1
và
2
chéo nhau.
III. GÓC
1. Góc giữa hai đường thẳng
Trong không gian với hệ toạ độ
Oxyz
, cho hai đường thẳng
1
và
2
có vectơ chỉ phương lần
lượt là
1 1 1 1 2 2 2 2
; ; , ; ;u a b c u a b c
. Khi đó, ta có:
1 2 1 2 1 2
1 2
2 2 2 2 2 2
1 1 1 2 2 2
cos , .
a a b b c c
abc abc
Nhận xét:
1 2 1 2 1 2 1 2
0
a a b b c c
.
Ví dụ 5: Tính góc giữa hai đường thẳng
1 2
,
biết:
1
2
1 1 2 2
1
4 3
: 2 3 và : 5
3 6
x t
x t
y t y t
z z
(
1 2
,t t
là tham
số)
Giải
Hai đường thẳng
1
và
2
có vectơ chỉ phương lần lượt là
1
(1; 3;0)
u
,
2
( 3;1;0)
u
. Ta
có:
1 2 2 2 2 2 2 2
|1 ( 3) ( 3) 1 0 0 | 2 3 3
cos , .
4 2
1 ( 3) 0 ( 3) 1 0
Suy ra
1 2
, 30
.
Ví dụ 6: Cho hai đường thẳng
1 2
1 1 2 3
: , : .
3 2 1 1 2 1
x y z x y z
Chứng minh rằng
1 2
.
Giải
Đường thẳng
1
và
2
có vectơ chỉ phương lẩn lượt là
1 2
(3;2;1), ( 1;2; 1)
u u
.
Ta có:
1 2
3 ( 1) 2 2 1 ( 1) 0
u u
.
Suy ra
1 2
.
2. Góc giữa đường thẳng và mặt phẳng
Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
có vectơ chỉ phương
1 1 1
; ;u a b c
và mặt phẳng
( )P
có vectơ pháp tuyến
222
; ;n a b c
. Gọi
( ,( ))P
là góc giữa đường thẳng
và mặt phẳng
( )P
. Khi đó,
1 2 1 2 1 2
2 2 2 2 2 2
1 1 1 2 2 2
| |
sin( ,( )) | cos( , ) | .
| | | |
a a b b c c
u n
P u n u n
abc abc
Điện thoại: 0946798489 CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Ví dụ 7: Cho mặt phẳng
( )P
có vectơ pháp tuyến
(1;2;2)n
và đường thẳng
có vectơ chỉ phương
(2;2; 1)u
. Tính sin của góc giữa đường thẳng
và mặt phẳng
( )P
. Góc giữa đường thẳng
và mặt phẳng
( )P
bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?
Giải
Ta có:
2 2 2 2 2 2
|1 2 2 2 2 ( 1) | 4
sin( ,( )) 9
1 2 2 2 2 ( 1)
P
. Suy ra
( ,( )) 26P
.
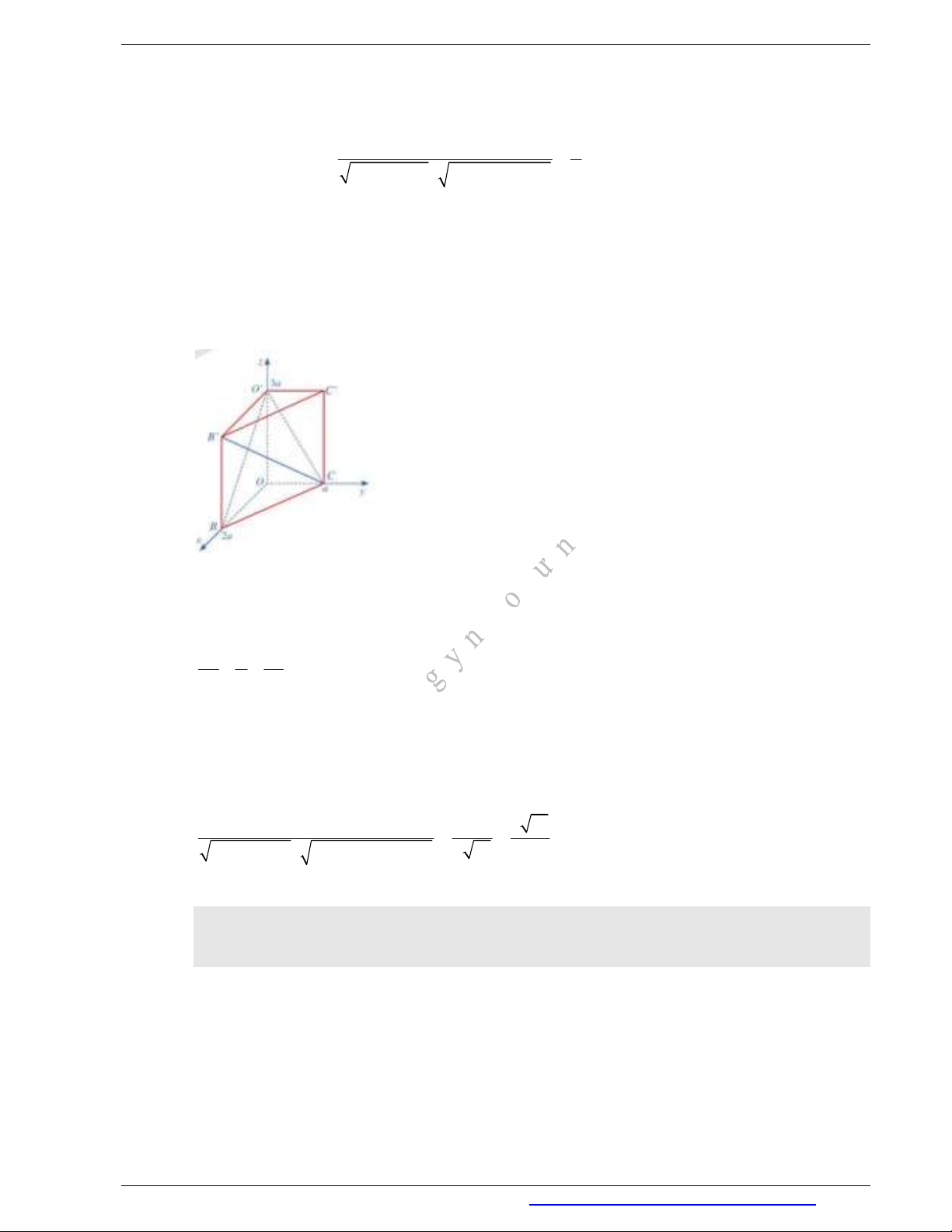
Ví dụ 8: Trong không gian với hệ tọa độ
Oxyz
, cho hình lăng trụ đứng
.OBC O B C
với
(0;0;0)O
,
(2 ;0;0), (0; ;0), (0;0;3 ), 0B a C a O a a
.
a) Xác định toạ độ của điểm
B
.
b) Viết phương trình mặt phẳng
O BC
.
c) Tính sin của góc giữa đường thẳng
B C
và mặt phẳng (
O BC
.
Giải.
a) Ta có:
(0;0;3 )BB OO a
. Suy ra
2
B
B
x x a
,
0, 0 3
B
B B
y y z a
, tức là
(2 ;0;3 )B a a
.
b) Vì
(2 ;0;0), (0; ;0), (0;0;3 )B a C a O a
nên mặt phẳng
O BC
có phương trình là
1 3 6 2 6 0.
2 3
x y z x y z a
a a a
c) Mặt phẳng
O BC
có một vectơ pháp tuyến là
(3;6;2)n
.
Do
(2 ;0;3 ), (0; ;0)B a a C a
nên
( 2 ; ; 3 )B C a a a
, suy ra vectơ
( 2 ; ; 3 )B C a a a
cùng
phương với vectơ
( 2;1; 3)u
. Vì thế vectơ
( 2;1; 3)u
là một vectơ chỉ phương của
đường thẳng
B C
. Suy ra sin của góc giữa đường thẳng
B C
và mặt phẳng
O BC
bằng:
2 2 2 2 2 2
| 3 ( 2) 6 1 2 ( 3) | 6 3 14 .
49
7 14
3 6 2 ( 2) 1 ( 3)
3. Góc giữa hai mặt phẳng
Góc giũa hai mặt phẳng
1
P
và
2
P
là góc giữa hai đường thẳng lần lượt vuông góc vôi hai
mặt phẳng đó, kí hiệu là
1 2
,P P
.
Ví dụ 9: Trong không gian, cho hình lập phương
ABCD A B C D
. Tính góc giữa hai mặt phẳng
( )ABCD
và (
CDA B
.
Giải.