CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025 Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN A. LÝ THUYẾT VÀ VÍ DỤ SÁCH GIÁO KHOA
1. ĐƯỜNG TIỆM CẬN NGANG
Đường thẳng 0
y y
gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số
( )y f x
nếu
0
lim ( )
x
f x y

hoặc
0
lim ( ) .
x
f x y

Ví dụ 1. Tìm tiệm cận ngang của đồ thị hàm số
3 2
( ) 1
x
y f x x
.
Giải
Ta có:
2
3
3 2
lim ( ) lim lim 3
1
11
x x x
xx
f x x
x
  
. Tương tự,
lim ( ) 3
x
f x

.
Vậy đồ thị hàm số
( )f x
có tiệm cận ngang là đường thẳng
3y
.
Ví dụ 2. Tìm các tiệm cận ngang của đồ thị hàm số
2
1
( ) x
y f x x
.
Giải
Ta có:
2 2
2 2
1 1 1
lim ( ) lim lim lim 1 1;
x x x x
x x
f x x x x
   
2 2
2 2
1 1 1
lim ( ) lim lim lim 1 1
x x x x
x x
f x x x x
   
.
Vậy đồ thị hàm số
( )f x
có hai tiệm cận ngang là
1y
và
1y
.
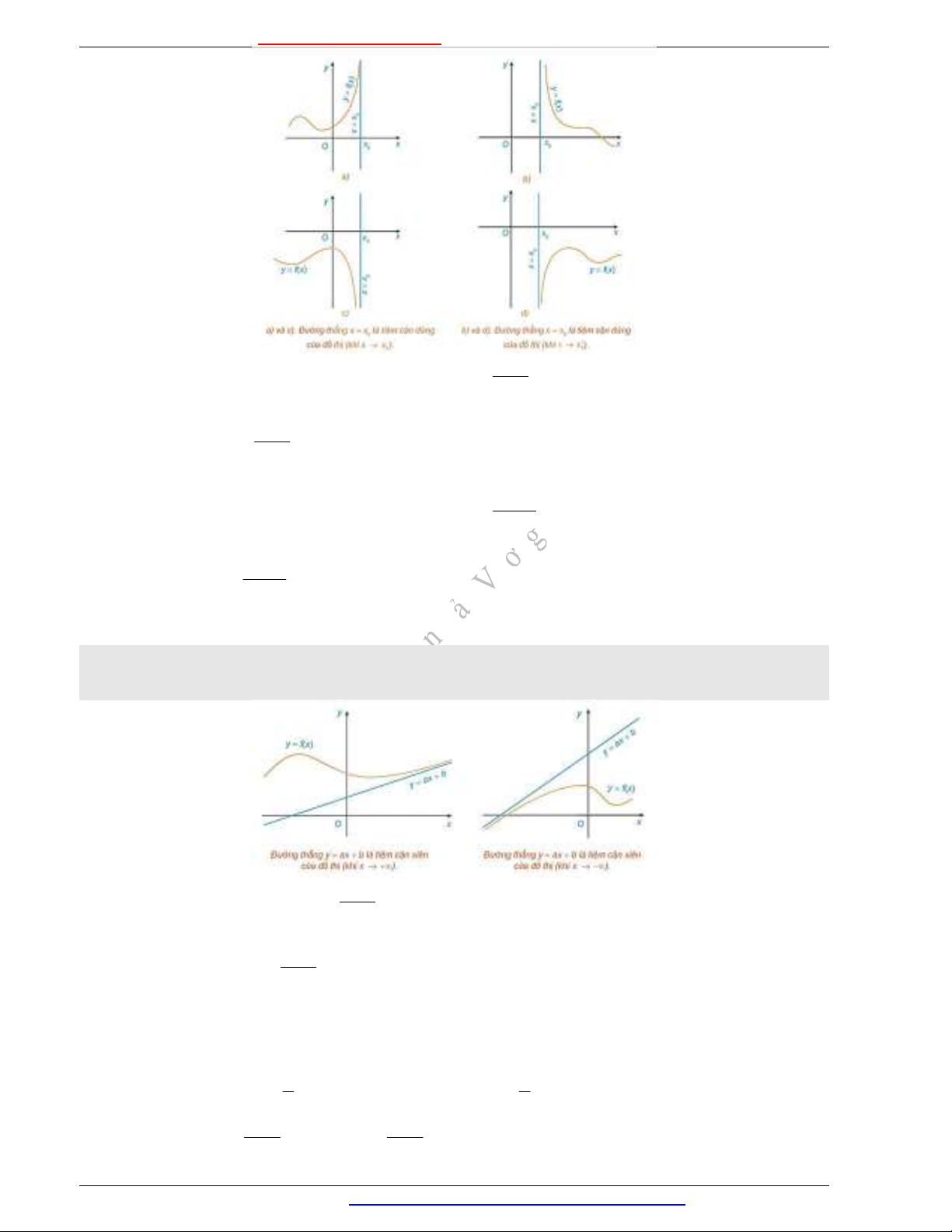
Nhận xét. Đồ thị hàm số
( )f x
như Hình.
2. ĐƯỜNG TIỆM CẬN ĐỨNG
Đường thẳng 0
x x
gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số
( )y f x
nếu ít nhất một trong các điều kiện sau được thoả mãn:
0000
lim ( ) ; lim ( ) ; lim ( ) ; lim ( ) .
x x x x x x x x
f x f x f x f x
   
CHUYÊN ĐỀ 4. TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
• Fanpage: Nguyễn Bảo Vương - https://www.nbv.edu.vn/
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Ví dụ 3. Tìm tiệm cận đứng của đồ thị hàm số
3
( ) 2
x
y f x x
.
Giải
Ta có:
2 2
3
lim ( ) lim 2
x x
x
f x x


. Tương tự,
2
lim ( )
x
f x

. Vậy đồ thị hàm số
( )f x
có tiệm cận
đứng là đường thẳng
2x
.
Ví dụ 4. Tìm tiệm cận đứng của đồ thị hàm số
2
2
( ) x
y f x x
.
Giải
Ta có:
2
0 0
2
lim ( ) lim
x x
x
f x x

. Tương tự,
0
lim ( )
x
f x

. Vậy đồ thị hàm số
( )f x
có tiệm cận đứng
là đường thẳng
0x
.
3. ĐƯỜNG TIỆM CẬN XIÊN
Đường thẳng
( 0)y ax b a
gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số
( )y f x
nếu
lim [ ( ) ( )] 0

x
f x ax b
hoặc
lim [ ( ) ( )] 0

x
f x ax b
Ví dụ 5. Cho hàm số
1
( ) 2
y f x x x
. Tìm tiệm cận xiên của đồ thị hàm số
( )f x
.
Giải
Ta có:
1
lim [ ( ) ] lim 0
2
x x
f x x x
 
. Tương tự
lim [ ( ) ] 0
x
f x x

.
Vậy đồ thị hàm số
( )f x
có tiệm cận xiên là đường thẳng
y x
.
Chú ý. Ta biết rằng nếu đường thẳng
( 0)y ax b a
là tiệm cận xiên của đồ thị hàm số
( )y f x
thì
lim [ ( ) ( )] 0
x
f x ax b

hoặc
lim [ ( ) ( )] 0
x
f x ax b

.
Do đó
1
lim[ ( ) ( )] 0
x
f x ax b x

hoặc
1
lim[ ( ) ( )] 0
x
f x ax b x

.
Từ đây suy ra
( )
lim
x
f x
ax

hoặc
( )
lim
x
f x
ax

.
Điện thoại: 0946798489 CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Khi đó, ta có
lim [ ( ) ]
x
b f x ax

hoặc
lim [ ( ) ]
x
b f x ax

.
Ngược lại, với
a
và
b
xác định như trên, đường thẳng
( 0)
y ax b a
là một tiệm cận xiên của đồ thị
hàm số
( )y f x
. Đặc biệt, nếu
0
a
thì đồ thị hàm số có tiệm cận ngang.
Ví dụ 6. Tìm tiệm cận xiên của đồ thị hàm số
2
( )
x x
y f x
.
Giải
Ta có:
2
2
( ) 2
lim lim 1
2 2
lim[ ( ) ] lim 2.
1
x x
x x
f x x x
ax x x
x
b f x x x
 
 
(Tương tự, ( )
lim 1, lim [ ( ) ] 2
x x
f x f x x
x
 
.)
Vậy đồ thị hàm số
( )f x
có tiệm cận xiên là đường thẳng
2y x
.
Nhận xét. Trong thực hành, để tìm tiệm cận xiên của hàm phân thức trong Ví dụ 6, ta viết:
2
2 4
( ) 2 .
1 1
x x
y f x x
x x
Ta có: 4
lim[ ( ) ( 2)] lim 0
1
x x
f x x
x
 
;
4
lim[ ( ) ( 2)] lim 0.
1
x x
f x x
x
 
Do đó, đồ thị hàm số
( )f x
có tiệm cận xiên là đường thẳng
2y x
.
PHẦN B. BÀI TẬP TỰ LUẬN
Dạng 1. Tìm các đường tiệm cận của đồ thị hàm số
Phương pháp.
1. Tìm tiệm cận ngang,tiệm cận đứng của đồ thị hàm
Thực hiện theo các bước sau
B1. Tìm tập xác định của hàm số
f x
B2. Tìm các giới hạn của
f x
khi
x
dần tới các biên của miền xác định và dựa vào định
nghĩa của các đường tiệm cận để kết luận
2. Tìm tiệm cận xiên của đồ thị hàm
Thực hiện theo các bước sau
B1. Tìm tập xác định của hàm số (đồ thị hàm số
f
chỉ có thể có tiệm cận xiên nếu tập xác định
của nó là là một khoảng vô hạn hay một nửa khoảng vô hạn)
B2. Sử dụng định nghĩa
Hoặc sử dụng định lí:
Nếu
( )
lim 0
x
f x a
x

và
lim [ ( ) ]
x
f x ax b

hoặc
( )
lim 0
x
f x a
x

và
lim [ ( ) ]
x
f x ax b

thì đường thẳng
y ax b
là tiệm cận xiên của đồ thị hàm số
f
CHÚ Ý: Đối với hàm phân thức:
( )
( )
P x
f x
Q x
trong đó
,
P x Q x
là hai đa thức của
x
ta
thường dùng phương pháp sau để tìm các đường tiệm cận của đồ thị hàm số
i) Tiệm cận đứng.
Nếu
0
0
( ) 0
( ) 0
P x
Q x
thì đường thẳng:
0
x x
là tiệm cận đứng của đồ thị hàm số
ii) Tiệm cận ngang
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Nếu bậc của
P x
bé hơn bậc của
Q x
thì đồ thị của hàm số có tiệm cận ngang là trục hoành
độ
Nếu bậc của
P x
bằng bậc của
Q x
thì đồ thị hàm có tiệm cận ngang là đường thẳng:
A
yB
trong đó
,A B
lần lượt là hệ số của số hạng có số mũ lớn nhất của
P x
và
Q x
Nếu bậc của
P x
lớn hơn bậc của
Q x
thì đồ thị của hàm số không có tiệm cận ngang
iii) Tiệm cận xiên
Nếu bậc của
P x
bé hơn hay bằng bậc của
Q x
hoặc lớn hơn bậc của
Q x
từ hai bậc trở lên
thì đồ thị hàm số không có tiệm cận xiên
Nếu bậc của
P x
lớn hơn bậc của
Q x
một bậc và
P x
không chia hết cho
Q x
thì đồ thị
hàm có tiệm cận xiên và ta tìm tiệm cận xiên bằng cách chia
P x
cho
Q x
và viết
( )
( )
R x
f x ax b
Q x
, trong đó
( ) ( )
lim 0 , lim 0
( ) ( )
x x
R x R x
Q x Q x
 
.
Suy ra đường thẳng:
y ax b
là tiệm cận xiên của đồ thị hàm số.
Câu 1. Cho hàm số
2
2 4
( ) 4
x
y f x x
có đồ thị là đường cong như Hình.
Các đường thẳng 2x và 2x có phải là các đường tiệm cận đứng của đồ thị hàm số đã
cho hay không? Vì sao?
Câu 2. Tìm tiệm cận ngang của đồ thị hàm số
2 1
( ) 2
x
y f x x
.
Câu 3. Giải thích vì sao đường thẳng
1x
là tiệm cận đứng của đồ thị hàm số
3 2
( ) 1
x
y f x x
?
Câu 4. Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
1
( ) 2
x
y f x x
.
Câu 5. Tìm tiệm cận đứng của đồ thị các hàm số sau:
a)
2
1
x
yx
b)
2
1
yx
.
Câu 6. Tìm tiệm cận ngang của đồ thị hàm số
2 1
1
x
yx
.
Câu 7. Đường cong ở Hình là đồ thị
( )C
của hàm số
2
5 7
( ) 3
x x
y f x x
.
Điện thoại: 0946798489 CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Chứng minh rằng đường thẳng
: 2
y x
là đường tiệm cận xiên của đồ thị hàm số
( )y f x
. Vẽ
lên cùng hệ trục toạ độ với
.C
Câu 8. Chứng minh rằng đường thẳng
2 1y x
là tiệm cận xiên của đồ thị hàm số
2
1
( ) 2 1
1
y f x x
x
.
Câu 9. Tìm tiệm cận xiên của đồ thị hàm số
2
3
( )
2
x x
y f x
x
.
Câu 10. Tìm tiệm cận xiên của đồ thị hàm số
2
3 1
( )
2
x x
f x
x
.
Câu 11. Tìm tiệm cận của hàm số:
a)
2 1
1
x
y
x
b)
2 4
1
x
y
x
c)
1
2 1
2
y x
x
d)
2
1
x
y
x
Câu 12. Tìm tiệm cận của hàm số:
a)
2
1
x
y
x
b)
2
2 2
y x x
c)
2
1
y x x
Câu 13. Tìm các đường tiệm cận của đồ thị các hàm số sau:
a)
1
1
5
y x
x
b)
2
2 6 1
3 1
x x
y
x
Câu 14. Tìm các đường tiệm cận của đồ thị các hàm số sau:
a)
2
2 3
4
x
y
x
b)
2
4
8
x
y
x
Câu 15. Tìm các đường tiệm cận của đồ thị các hàm số sau:
a)
3
2 4
2 3
1
x
y x
x
b)
3
2
2
2
x
y
x x
Câu 16. Tìm các đường tiệm cận của đồ thị các hàm số sau:
a)
3
2
2 4
4
x x
y
x
b)
2
2
2
2 3
x x
y
x x
Câu 17. Tìm các đường tiệm cận của đồ thị các hàm số sau:
a)
2
4 3 2
y x x x
b)
2
3 4
y x x