1
Chương 2:
PHÂN TÍCH TRONG MIỀN THỜI GIAN
Mô hình tổng quát của hệ thống xử lý tín hiệu rời rạc thời gian (DTSP), hoặc xử lý tín hiệu số (DSP),
được mô tả như hình 2.1. Hệ thống áp tín hiệu vào và cho tín hiệu ra khác só với tín hiệu vào tại một
số đặc điểm (biên độ, tần số, pha…). Ngõ ra là đáp ứng của hệ thống. Một hệ thống có thể có nhiều
hơn một đầu vào và một đầu ra. Hệ thống thường nói đến nhất là lọc số.
Trong chương trước, một hệ thống được mô tả (hoặc trình bày) bởi phương trình tín hiệu vào
ra. Trong chương này, chúng ta sẽ thấy hệ thống được mô tả ngắn gọn bằng đáp ứng xung của nó. Ngõ
ra là kết quả nhân chập tín hiệu vào và đáp ứng xung. Đáp ứng chuyển tiếp cũng được nhắc đến một
cách ngắn gọn. Phần kế tiếp sẽ nói đến lọc số và giải phương trình
2.1 ĐÁP ỨNG XUNG
Ta tìm cách khác để mô tả ngắn gọn hệ thống rời rạc thời gian.
Xét tín hiệu mẫu đơn vị (Hình.2.2)
(n) = 1 , n = 0
0 , n
0
Khi mẫu dịch chuyển đến thời điểm k trong tương lai (k > 0) tín hiệu là
(n-k) = 1 , n = k
0 , n
k
Khi mẫu dịch chuyển về quá khứ tại thời điểm –k (k > 0), tín hiệu là
(n + k) = 1 , n = -k
0 , n
-k
Bây giờ, xem sự diễn tả một tín hiệu theo xung mẫu đơn vị. Trong hình 2.3 giá trị của x(n) khi n = 1
và 3, ta có thể viết (1.6).
x(n = 1) = x(1)
(n - 1) = 3 x 1 = 3
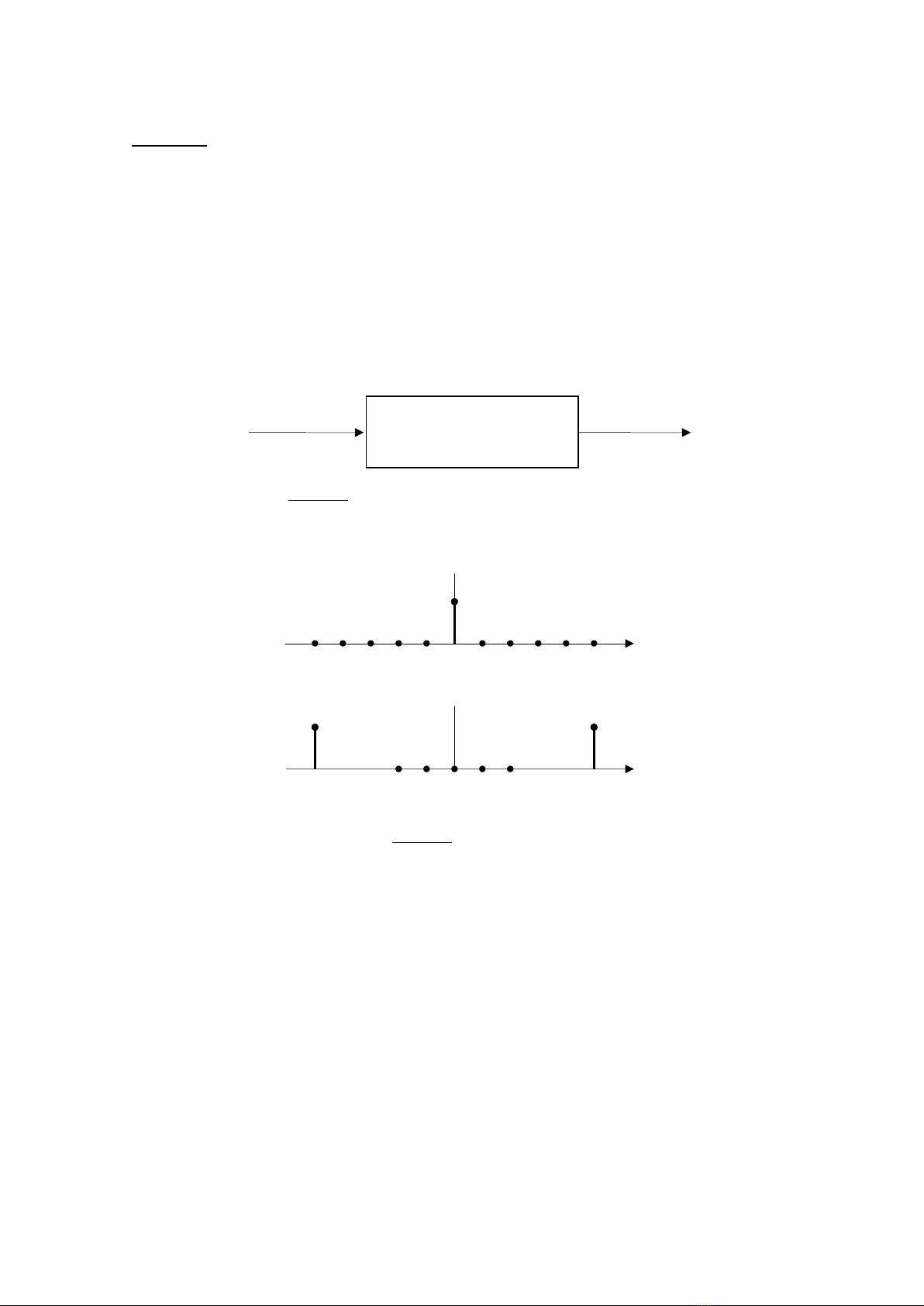
Hệ thống
LTI (LSI)
Tín hiệu vào
Tín hiệu ra
Hình.2.1
: Mô hình tổng quát của hệ thống DTSP (hoặc DSP)
x(n)
y(n)
(n)
1
n
-2
0
2
(a) Xung tại n = 0
-1
3
1
n
0
2
1
-2
-1
-3
1
1
(n+k)
(n-k)
(b) Xung tại n = k và tại n = -k
-k
k
(2.1)
Hình.2.2: Mẫu đơn vị
2
Giống như vậy khi n = 2
[
x(n = 2) = x(2)
(n – 2) = 2 x 1 = 2
Vì vậy, tín hiệu tổng quát x(n) có thể diễn tả như
k
knkxnx
(2.2)
2.1.1 Đáp ứng xung
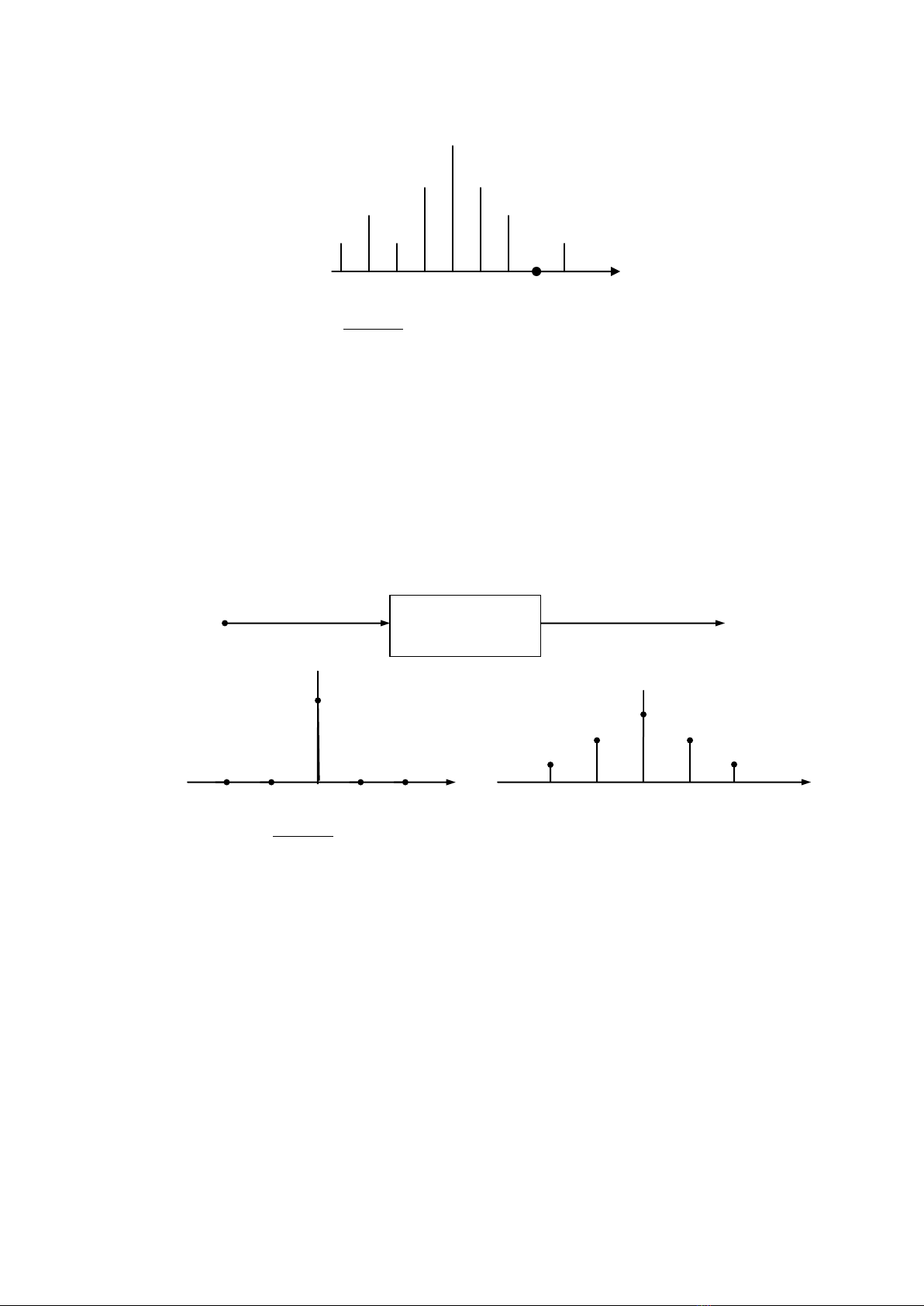
Đáp ứng xung của một tín hiệu định nghĩa như ngõ ra (đáp ứng), chú thích h(n), khi ngõ vào là mẫu
đơn vị
(n). Đáp ứng xung có thể thực hoặc phức, nhưng thường là thực. Hình 2.4 là một ví dụ
2.1.2 Hệ thống FIR và IIR
Khi kích một mẫu đơn vị
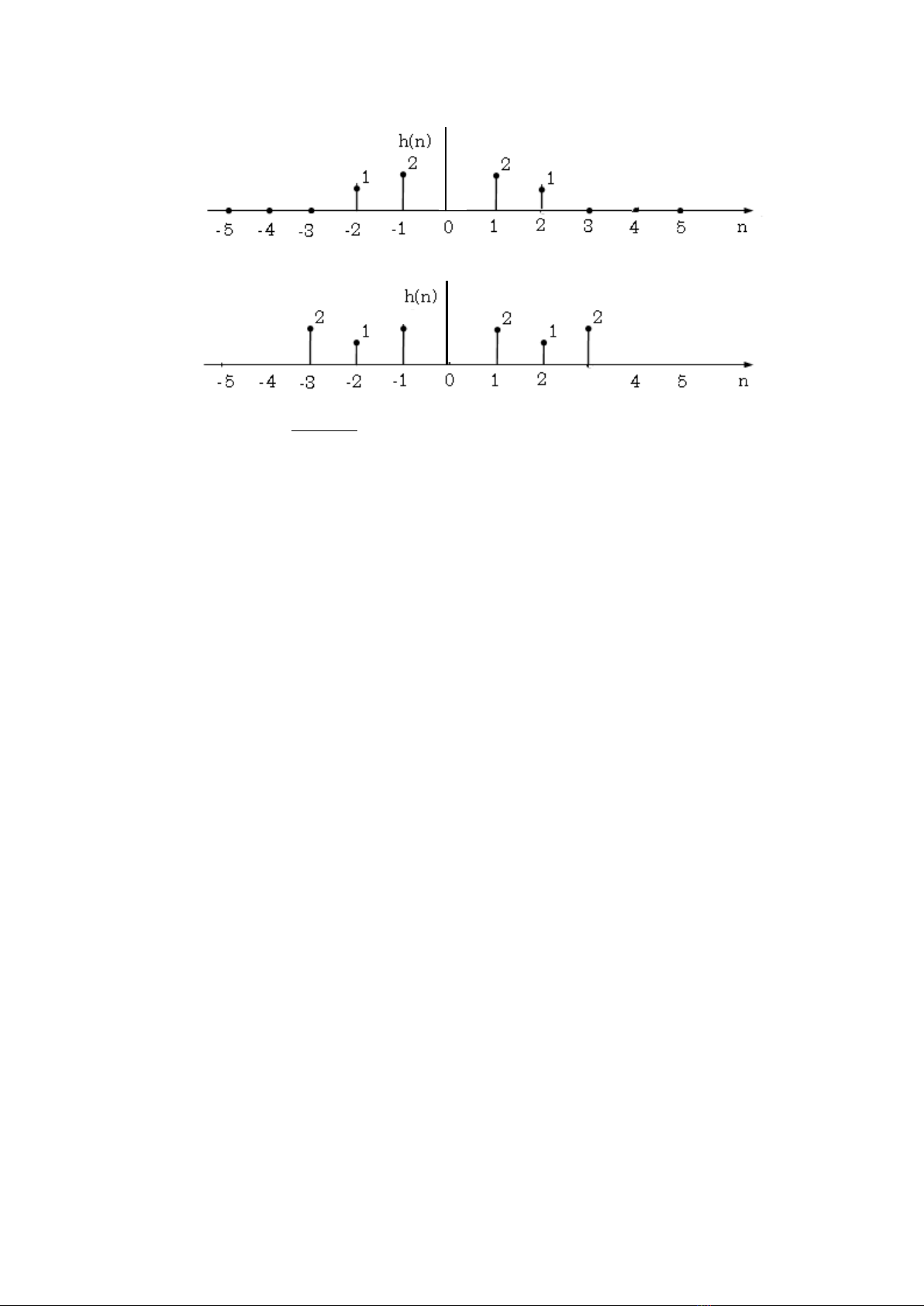
(n), đáp ứng xung h(n) của hệ thống có thể hiện hữu hữu hạn (hình 2.5a)
hoặc vô hạn (hình 2.5b). Trường hợp đầu hệ thống có đáp ứng xung hữu hạn (FIR), và trường hợp sau
hệ thống có đáp ứng xung lâu vô hạn (IIR).
Hoặc, có thể phân loại hệ thống thành dạng đệ qui hoặc không đệ quy thay vì IIR hoặc FIR. Ta sẽ thảo
luận sau.
Nhân quả (Phần 1.6.2) của một hệ thống thể hiện trên đáp ứng xung của nó. Với hệ thống
nhân quả h(n)= 0 khi n<0 (hoặc n
-1), ngược lại hệ thống là phi nhân quả. Cả hai hệ thống trong
hình 2.5 là phi nhân quả.
2.1.3 Tính đáp ứng xung từ phƣơng trình tín hiệu vào
Từ đinh nghĩa của đáp ứng xung ta có thể áp một mẫu đơn vị vào hệ thống và lấy tín hiệu ra, hoặc đáp
ứng xung. Mặc khác, ta có thể tính nó từ phương trình tín hiệu như trình bày ở đây. Ở đây có nhiều
cách khác nhau để tính đáp ứng xung.
.
.
.
.
.
.
.
.
1
2
1
3
4
3
2
1
0
n
x(n)
Hình.2.3 : Tín hiệu ví dụ
-4 -3 -2 -1 0 1 2 3 4
n
1
(n)
0
1
2
-1
-2
Hình.2.4 : Định nghĩa và ví dụ của đáp ứng xung
Ra
Vào
Hệ thống
S
x(n) = (n)
y(n) = h(n)
. . .
. . .
0
1
2
-1
-2
n
h(n)
3
Ví dụ 2.1.1
Tìm đáp ứng xung của hệ thống khi phương trình tín hiệu vào ra được cho bởi
y(n) = 0.8y(n – 1) + x(n)
Giải
Thay x(n) bằng
)(n
thì y(n) là h(n):
h(n) = 0.8h(n – 1) +
)(n
Nhớ rằng
)(n
= 1 khi n = 0, và bằng 0 ở những giá trị khác, giả sử hệ thống nhân quả, có nghĩa h(n)
= 0 với n < 0, ta có
[
h(0) = 0.8h(-1) +
)0(
= 1
h(1) = 0.8h( 0) +
1
= 0.8
h(2) = 0.8h( 1) +
)2(
= 0.8
2
h(3) = 0.8h( 2) +
)3(
= 0.8
3
. . .
h(n) = 0.8
)(nu
n
Hệ thống là IIR và ổn định vì h(n) hội tụ (xem phần 2.4). Thường ta không lấy kết quả cuối cùng như
trên (xem ví dụ 2.6.4).
2.1.4 Tìm phƣơng trình tín hiệu vào ra từ đáp ứng xung
Khi biết đáp ứng xung của hệ thống, ta có thể tính phương trình tín hiệu vào ra, minh họa bằng ví dụ
sau:
Ví dụ 2.1.2
Đáp ứng xung của hệ thống tuần hoàn với chu kỳ 3 mẫu.
h(n) = [ 1, 2, 3; 1, 2, 3; 1, 2, 3; 1, 2 ... ]
Tìm phương trình tín hiệu vào ra.
Giải
Sự trễ được cho bởi 3 mẫu.
Hình.2.5: Ví dụ của hệ thống (a) FIR, (b) IIR
°
° ° °
° ° °
2
°
°
3
3

4
h(n - 3) = [ 0, 0, 0; 1, 2, 3; 1, 2, 3; 1, 2 … ]
Tính sự khác nhau
h(n) - h(n - 3) = [ 1, 2, 3; 0, 0, 0; 0, 0 … ]
=
)2(3)1(2)( nnn
Thì
)2(3)1(2)()3()( nnnnhnh
Phương trình tín hiệu vào ra là
y(n) = y(n - 3) + x(n) + 2x(n - 1) + 3x(n - 2)
2.2 NHÂN CHẬP SỐ
Trên là định nghĩa đáp ứng xung. Trong phần này ta sẽ thấy một cách ngắn gọn tầm quan trọng của
đáp ứng xung và đây cũng là đặc điểm của hệ thống LTI (hoặc LSI).
2.2.1 Tổng nhân chập
Với tín hiệu vào được diễn tả theo mẫu đơn vị trong công thức (2.2), ngõ ra của hệ thống S là
y(n) = S[x(n)] = S
k
knkx
Với một hệ thống tuyến tính
kk
knSkxknkxSny
(2.3)
Kế đến, nếu hệ thống bất biến thời gian
S[(n - k)] = h(n - k) (2.4)
Thì ngõ ra là
k
knhkxny
(2.5)
Đây là tổng nhân chập (hoặc tổng chập) trong DTSP (hoặc DSP), tương tự với tích chập trong hệ
thống tương tự. Chú ý, dấu sao được sử dụng để chú thích cho nhân chập.
k
knhkxnhnxny
(2.6)
Điều này có nghĩa nếu biết đáp ứng xung h(n) của một hệ thống, ta có thể tìm ngõ ra tín hiệu y(n) với
bất kỳ tín hiệu vào x(n). Vì điều này, đáp ứng xung được xem là đặc tính thời gian (hoặc đặc điểm)
của hệ thống. Tổng được lấy từ
đến
, nhưng trong thực tế thường là tổng hữu hạn, nên việc
tính toán được thực hiện dễ dàng.
2.2.2 Cách tính tổng nhân chập
Với hệ thống tương tư, nhân chập được tính bằng tích phân. Công việc này dễ hơn trong hệ
thống số vì nhân chập được tính bằng cách lấy tổng. Nó là một ý kiến hay để bắt đầu tính bằng phương
pháp giản đồ. Những bước gồm:
1. Đổi biến số n thành biến số k, viết x(k), h(k). Chọn x(k) cố định, h(k) dịch.
2. Lấy ảnh gương của h(k) tức tạo ảnh h(-k) đối xứng qua h(k) qua trục biên độ. Tạo ảnh gương
còn gọi là gấp ảnh. Ở n=0, tính tổng nhân chập
k
khkxy 0
.
3. Dịch chuyển h(-k) bằng cách thêm thông số trược n tức tạo h(n-k). Cho n=1, 2, 3, …. Để h(n-
k) dịch chuyển phải (về tương lai), ở mỗi trị số của n tính tổng nhân chập. Tăng n lên cho đến
khi thấy tổng chập tiếp tục bằng không (tức h(n-k) đã trượt qua khỏi x(k)).
5
4. Bây giờ đảo hướng dịch chuyển n= -1, -2, -3... để dịch h(n-k) về trái (về quá khứ), ở mỗi trị
số của n tính tổng nhân chập cho đến khi thấy tổng nhân chập tiếp tục là không (tức h(n-k) đã
trược qua khỏi x(k)).
Quá trình tính tổng nhân chập có thể được tổng kết như sau: trộn-dịch-nhân-cộng
Ví dụ 2.2.1
Tín hiệu vào và đáp ứng xung tương ứng là:
x(n) = [0, 1, 2, 3, 1, 0]
h(n) = [0, 1, 2, 2, 0]
Biểu tượng in đậm là mẫu tại gốc. Tìm ngõ ra tín hiệu y(n) = x(n)
h(n).
Giải
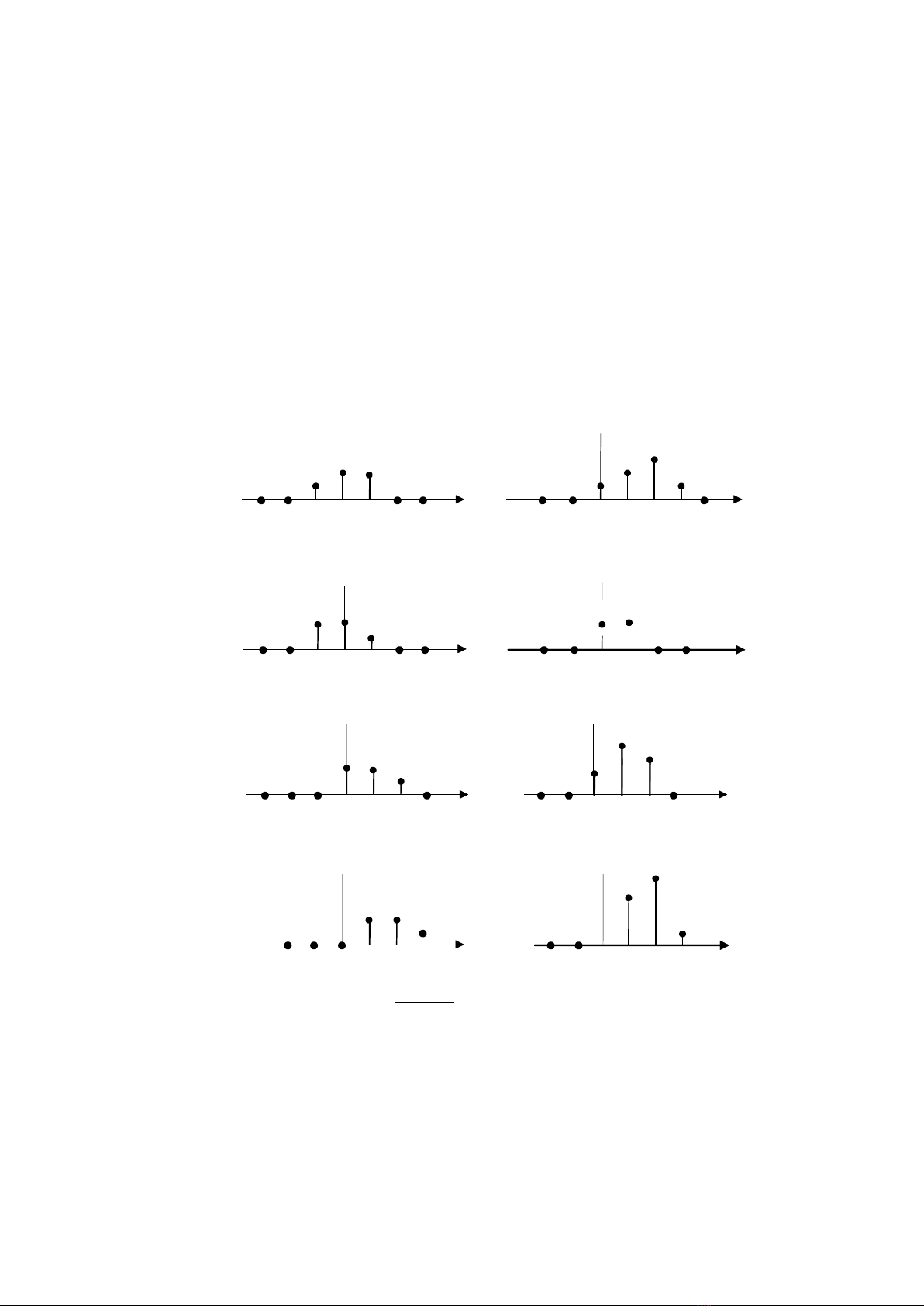
Xử lý qua những bước đã nêu bên trên
k
k
x(k)
h(k)
3
2
1
0
-1
-2
1
3
2
1
2
1
0
-1
-2
2
2
1
-3
3
4
k
9
k
k
x(k)h(1-k)
h(1-k)
3
2
1
0
-1
-2
4
2
2
1
0
-1
-2
2
2
-3
3
1
3
k
11
k
k
x(k)h(2-k)
h(2-k)
3
2
1
0
-1
-2
6
4
2
1
0
-1
-2
2
3
2
1
1
Tiếp tục, ta có
k
8, 2, 0. Kế đến, đảo ngược hướng dịch như bước 4. Tín hiệu ra cuối cùng là
y(n) = [ ... 0, 1, 4, 9, 11, 8, 2, 0, ... ]
Phƣơng pháp chuỗi (Vector)
Ở đây có những phương pháp khác tính nhân chập số. Phương pháp giản đồ là cơ bản và minh hoạ rõ.
Một số tác giả thích phương pháp ma trận. Bên cạnh, phương pháp chuỗi (vector) ít tốn thời gian và là
k
4
k
k
x(k)h(-k)
h(-k)
3
2
1
0
-1
-2
2
2
2
1
0
-1
-2
2
1
2
-3
3
Hình.2.6 : Ví dụ 2.2.1
(1)
(2)
n = 0
(3a)
n = 1
(3b)
n = 2