QUAN HỆ GÓC VÀ CẠNH ĐỐI DIỆN TRONG MỘT
TAM GIÁC.
A. Mục tiêu:
- Nắm vững nội dung hai định lý, vận dụng được chúng trong những tình
huống cần thiết, hiểu được phép chứng minh của định lí 1.
- Biết vẽ hình đúng yêu cầu và dự đoán nhận xét các tính chất qua hình vẽ.
- Biết diễn đạt một định lí thành một bài toán với hình vẽ, giả thiết và kết
luận.
B. Chuẩn bị: Bảng phụ ghi đề bài.
C. Bài tập
Tiết 21:
Bài 1:
a. So sánh các góc của tam giác PQR biết rằng PQ = 7cm; QR = 7cm; PR =
5cm
b. So sánh các cạnh của tam giác HIK biết rằng H = 750; K = 350
Giải:
a. Từ hình vẽ bên ta có: PQ = RP P
PQR
cân tại Q
R = P
QR > PR
P > Q 7 5
(quan hệ giữa cạnh và góc đối diện)
vậy R = P > Q Q R
b. I = 1800 - (750 + 350) = 1800 - 1100 = 700
H > I > K
IK > HK > HI (quan hệ giữa cạnh và góc đối diện)
Bài 2: Cho tam giác ABC. Chứng minh rằng AB + AC > BC
Giải:
Trên tia đới của tia AB lấy điểm D D
sao cho AD = AC
Ta có: AD = AC
ADC
cân đỉnh D
ADC = ACD (1) A
Tia CA nằm giữa hai tia CB và CD
Do đó: BCD > ACD (2)
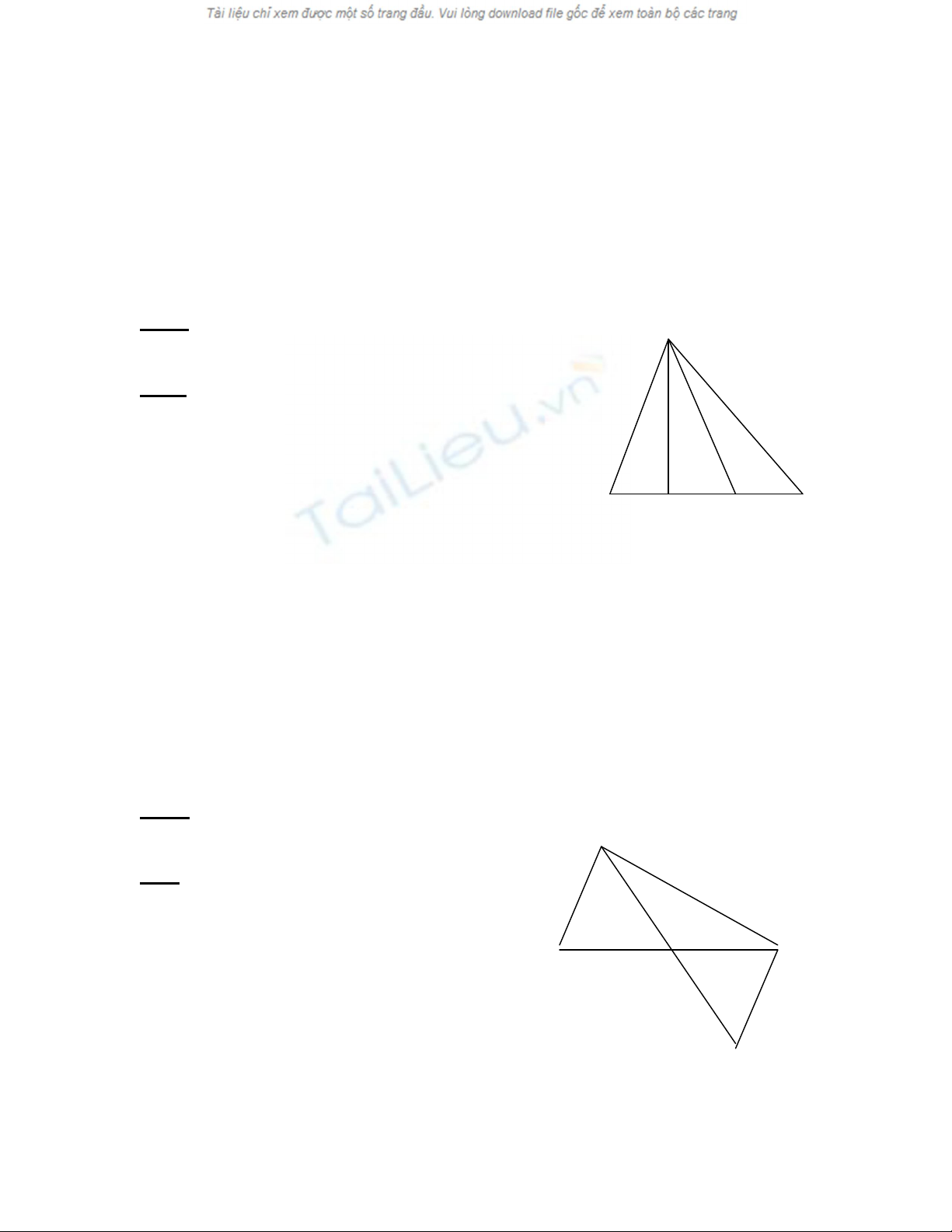
Từ (1) và (2) ta có: BCD > ADC B
C
Xét tam giác DBC có BCD > BDC
suy ra DB > BC (quan hệ giữa góc và cạnh đối diện trong tam giác) (3)
mà DB = AB + AD = AB + AC (4)
Từ (3) và (4) ta có: AB + AC > BC
Bài 3: Cho tam giác ABC, A = 900. Trên tia đối của tia AC lấy D sao cho
AD < AC. Nối B với D. Chứng minh rằng: BC > BD B
Giải:
Trên tia AC lấy điểm E sao cho AE = AD
Ta có: AE < AC (Vì AD < AC)
Nên E nằm giữa A và C
Mà BA
DE và DA = AE D A E
C
BDE
cân đỉnh B
BDE = BEA
Ta có: BEA > BCE (BEA là góc ngoài của tam giác BEC)
Do đó: BDC > BCD
Xét tam giác BDC có: BDC > BCD
Suy ra: BC > BD (quan hệ giữa góc và cạnh đối diện trong một tam giác)
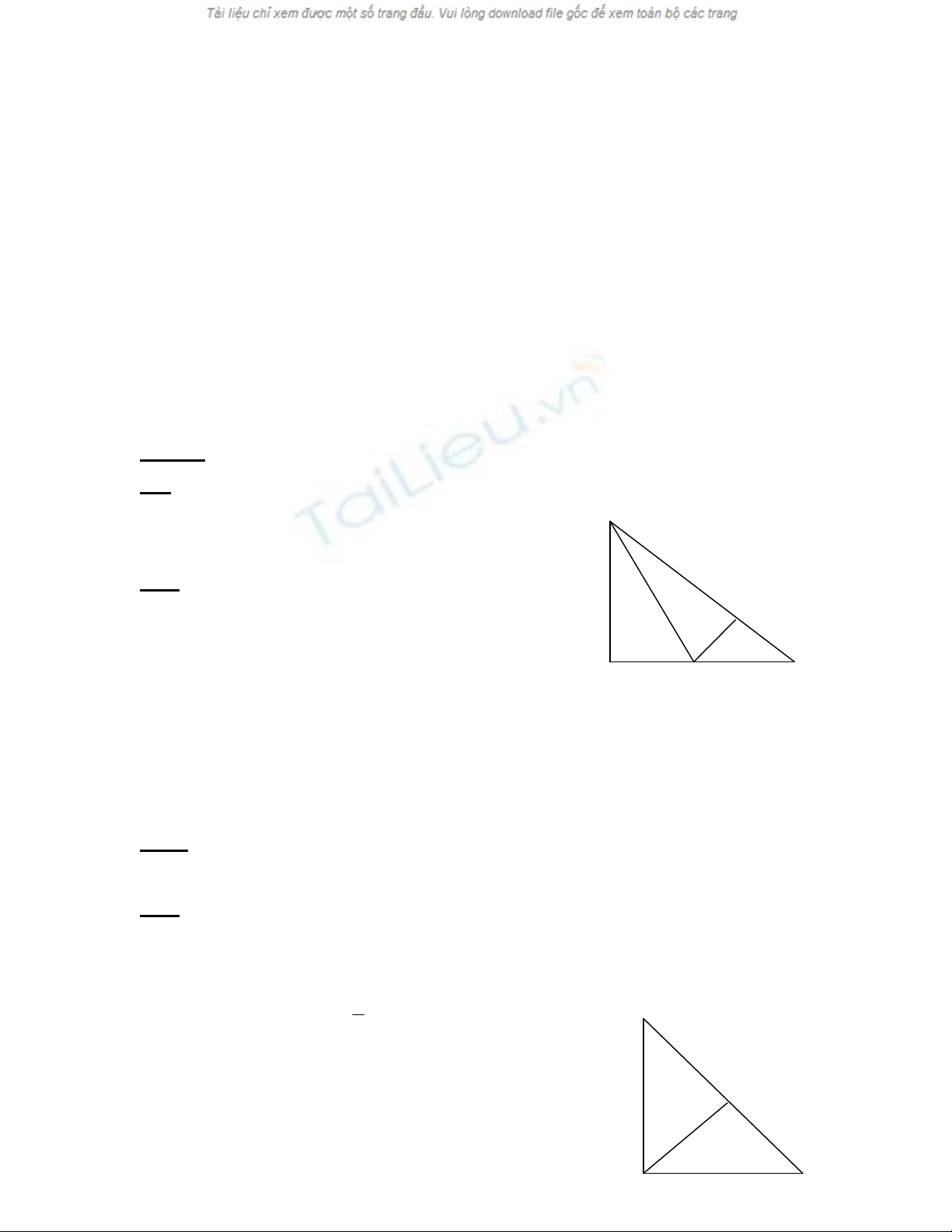
Bài 4: Cho tam giác ABC có AB < AC, M là trung điểm của cạnh BC. So
sánh BAM và MAC A
Giải:
Vẽ tia đối của tia MA và trên đó
lấy điểm D sao cho MD = MA
Xét tam giác MAB và tam giác MDC có: B M C
MA = MD; AMB = DMC (đối đỉnh)
MB = MC (M là TĐ của cạnh BC)
Do đó: MDCMAB
(c.g.c) D
Suy ra: AB = CD; BAM = MDC
Ta có: AB = CD; AB < AC
CD < CA
Xét tam giác ADC có: CD < AC
MAC < MDC (quan hệ giữa góc và
cạnh đối diện trong tam giác)
Mà MAC < MDC và BAM = MDC
Suy ra: MAC < BAM
Tiết 22:
Bài 5: Cho tam giác ABC vuông ở A, tia phân giác của góc B cắt AC ở D.
So sánh các độ dài AD, DC. B
Giải:
Kẻ DH
BC H
HBD
ABD
(cạnh huyền - góc nhọn) A D C
AD = DH
DHC
vuông tại H
DH < DC
DHC
(cạnh góc vuông nhỏ hơn cạnh huyền)
suy ra: AD < DC
Bài 6: Chứng minh rằng nếu một tam giác vuông có một góc nhọn bằng 300
thì cạnh góc vuông đối diện với nó bằng nửa cạnh huyền.
Giải:
Xét tam giác ABC có A = 900; B = 300
Cần chứng minh: AC =
2
1BC B
Trên BC lấy điểm D sao cho CD = CA
Tam giác ACD còn có: C = 600, AD = AC = CD D
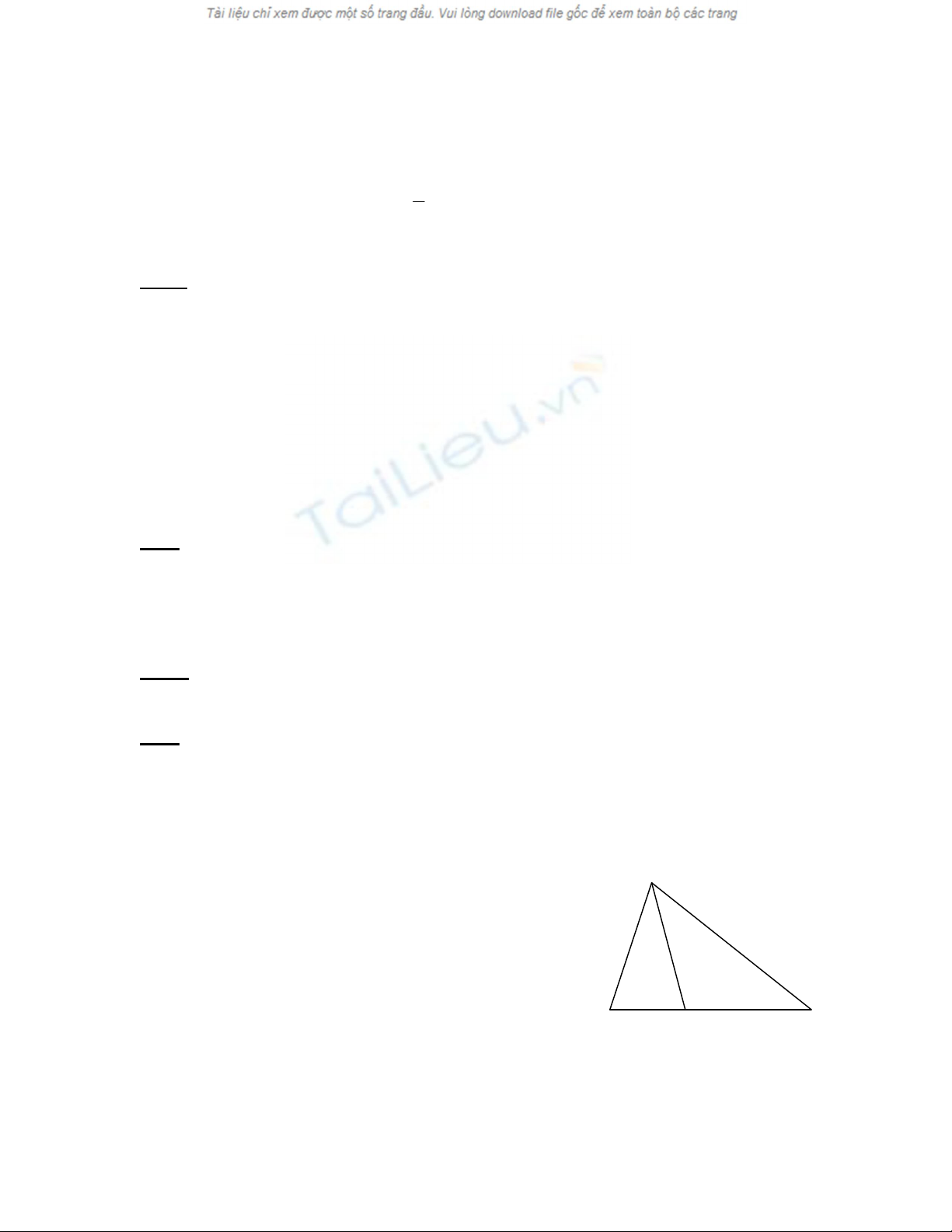
Tam giác ABD có B = 300; A2 = 300
nên là tam giác đều
suy ra AD = BE. Do đó: AC =
2
1BC A
C
Bài 7: Cho tam giác ABC có A = 850, B = 400
a. So sánh các cạnh của tam giác ABC
A. AB < BC < AC C. AB < AC < BC
B. BC < AC < AB D. AC < AB < BC
b. Trên tia đối của yia AB lấy điểm D sao cho AD = AC. Trên tia đối của tia
BA lấy điểm E sao cho BE = BC. So sánh độ dài các đoạn CD; CB; CE
A. CE < CB < CD C. CD < CE < CB
B. CB < CE < CD D. CD < CB < CE
Giải: a. Chọn D
Vì C = 1800 - (A + B) = 1800 - (85 + 40) = 55
Khi đó nhận thấy rằng B < C < A
Ac < AB < BC
b. Chọn D
Bài 8: Cho tam giác ABC tia phân giác của góc D cắt AC tại D. So sánh độ
dài của AB và BC, biết BDC tù.
Giải:
Để so sánh độ dài của AB và BC ta cần đi so sánh hai góc C và A.
Theo giả thiết ta có: BDC tù
D1 > 900
2D1 > 1800
Trong tam giác ABD ta có: D1 = A + B2 (1) B
Trong tam giác BCD ta có: D1 + B1 + C1 = 1800 (2)
Công theo vế (1) và (2) ta được:
2D1 + B1 + C = A + B2 + 1800
A - C = 2D1 - 1800 > 0
A > C
BC > AB A D
C

Tiết 23:
Bài 9: Cho góc xOy = 600, điểm A nằm trong góc xOy. Vẽ điểm D sao cho
Ox là đường trung trực của AB. Vẽ điểm C sao cho Oy là đường trùng trực
của AC.
a. Khẳng định OB = OC là đúng hay sai?
A. Đúng B. Sai
b. Tính số đo góc BOC
A. 600; B. 900; C. 1200; D. 1500
Giải: a. Chọn A
Vì OA = OB (vì Ox là đường trung trực của AB)
OA = OC (vì Oy là đường trung trực của AC)
Do đó: OB = OC
b. Chọn C vì tam giác OAB cân ở O nên O1 = O2
Tam giác OAC cân ở O nên O3 = O4
Khi đó: BOC = O1 + O2 + O3 + O4 = 2O2 + 2O3 = 2(O2 + O3)
= 2(xOy) = 2. 600 = 1200
Vậy ta có: BOC = 1200
Bài 10:
a. Cho tam giác ABC và tam giác A1B1C1 có AB = A1B1. AC = A1C1 và
BC > B1C1. So sánh số đo của hai góc A và A1
Giải: Theo giả thiết ta có: AB = A1B1; AC = A1C1 và BC > B1C1
Thì A > A1 (quan hệ giữa các cạnh đối diện trong tam giác)
b. Cho hai tam giác ABC và A1B1C1 có AB = A1B1. AC = A1C1 và A > A1.
Chứng minh rằng BC > B1C1
Giải: Xét tam giác ABC và tam giác A1B1C1
Có AB = A1B1; AC = A1C1 và A > A1 (gt)
Suy ra: BC > B1C1 (quan hệ giữa cạnh và góc đối diện trong 1 tam giác)
Bài 11: Cho tam giác ABC trung tuyến AM. Lấy điểm M bất kì trên tia đối
của tia MA. So sánh độ dài CD và BD. A
Giải:
Ta lần lượt nhận thấy
















