Sắp xếp trộn
mergesort
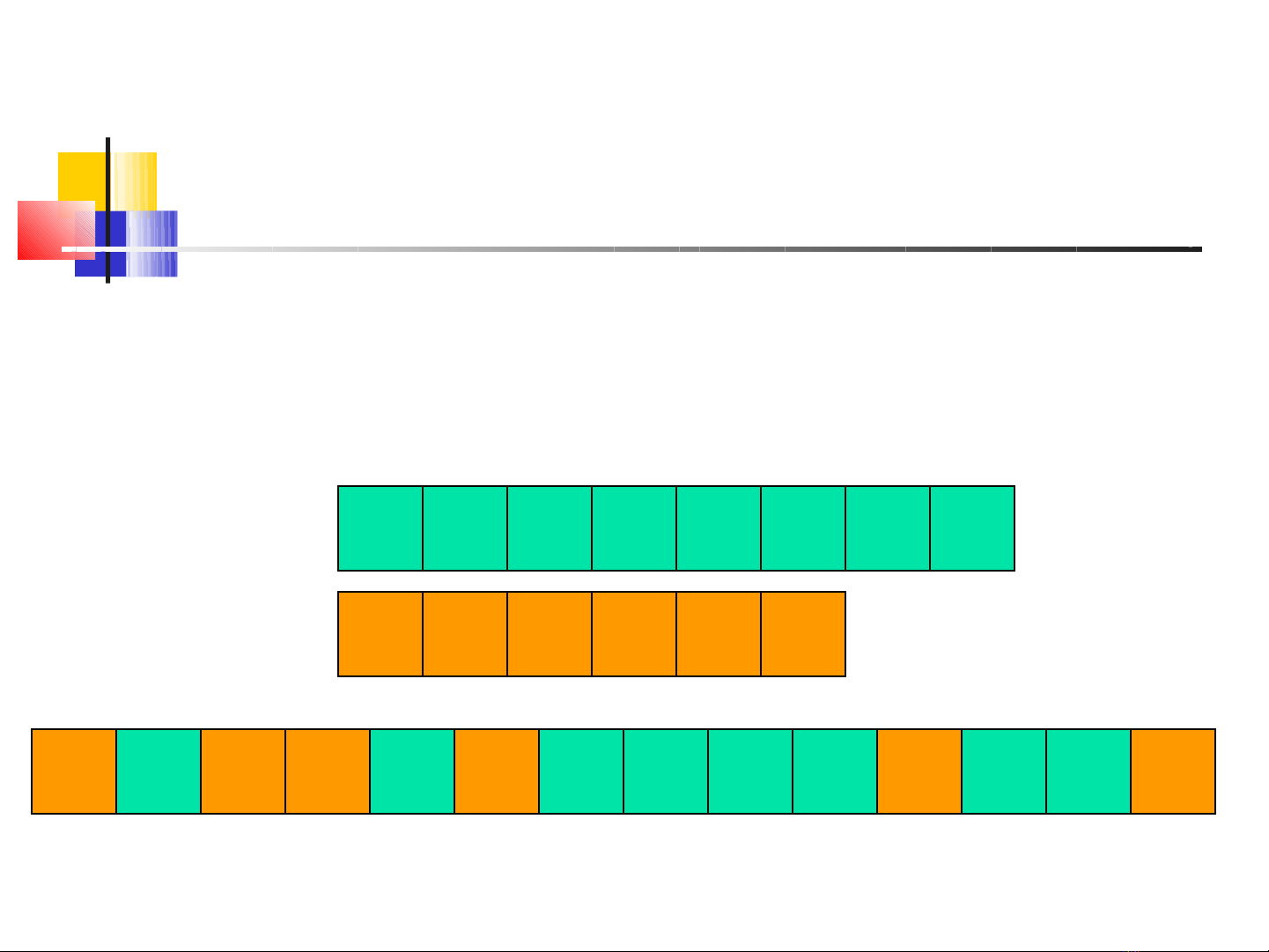
Tư tưởng trộn
Có 2 mảng đã được sắp xếp chiều dài
N,M
Tạo ra 1 mảng chung được sắp xếp
2 5 7 8 9 10 13 14
1 4 6 11 20
1 2
3
3 4 5 6 7 8 9 10 11 13 14 20
Bước 1: chọn min của 2 phần tử đầu
dãy chép qua mảng kết quả
Bước 2: hủy phần tử min
Bước 3: nếu chưa đến cuối mảng trở về
bước 1
Nếu đến cuối mảng: chép phần còn lại
của mảng kia vào mảng kết quả
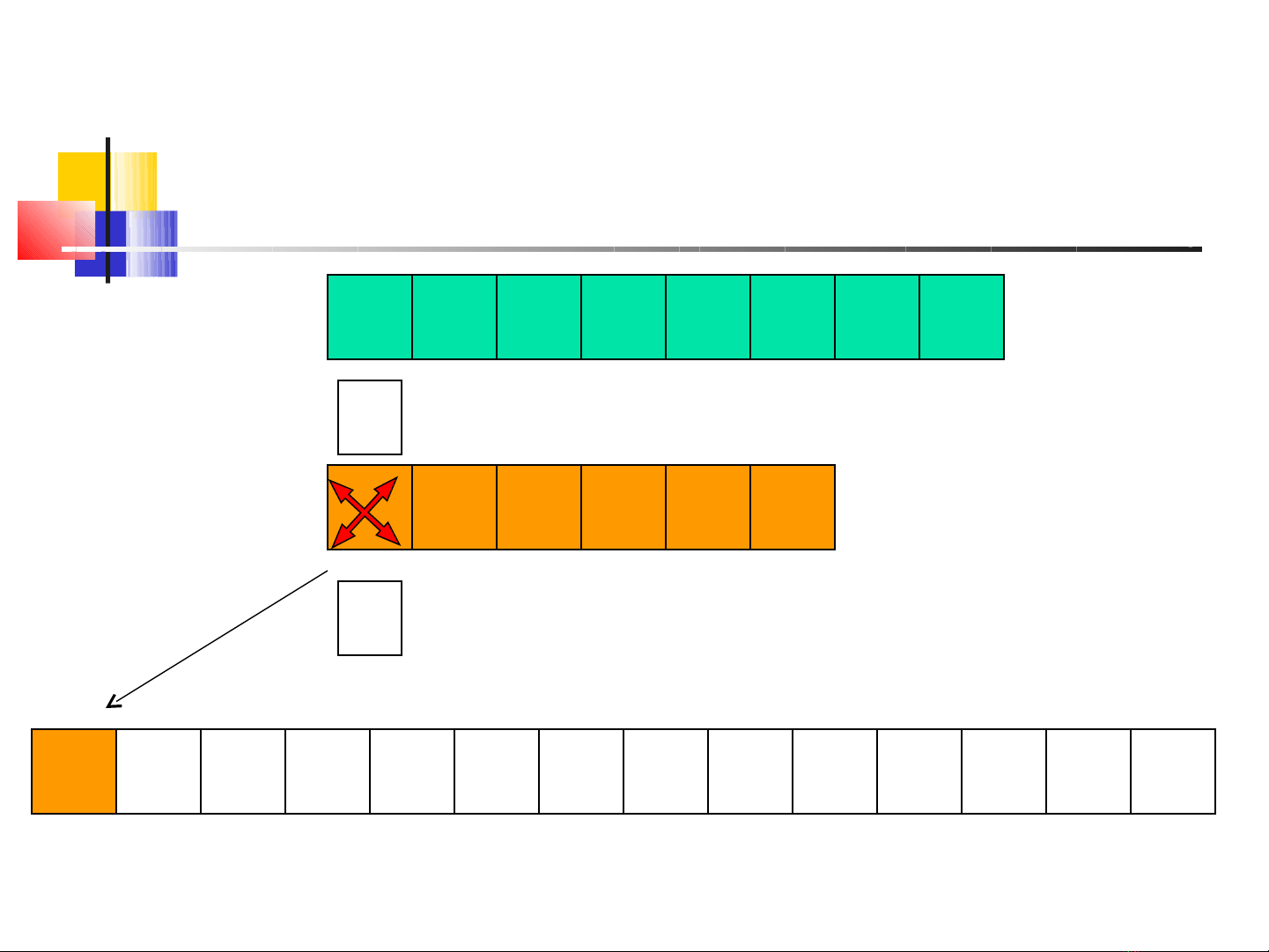
2 5 7 8 9 10 13 14
1 4 6 11 203
i=0
j=0
1
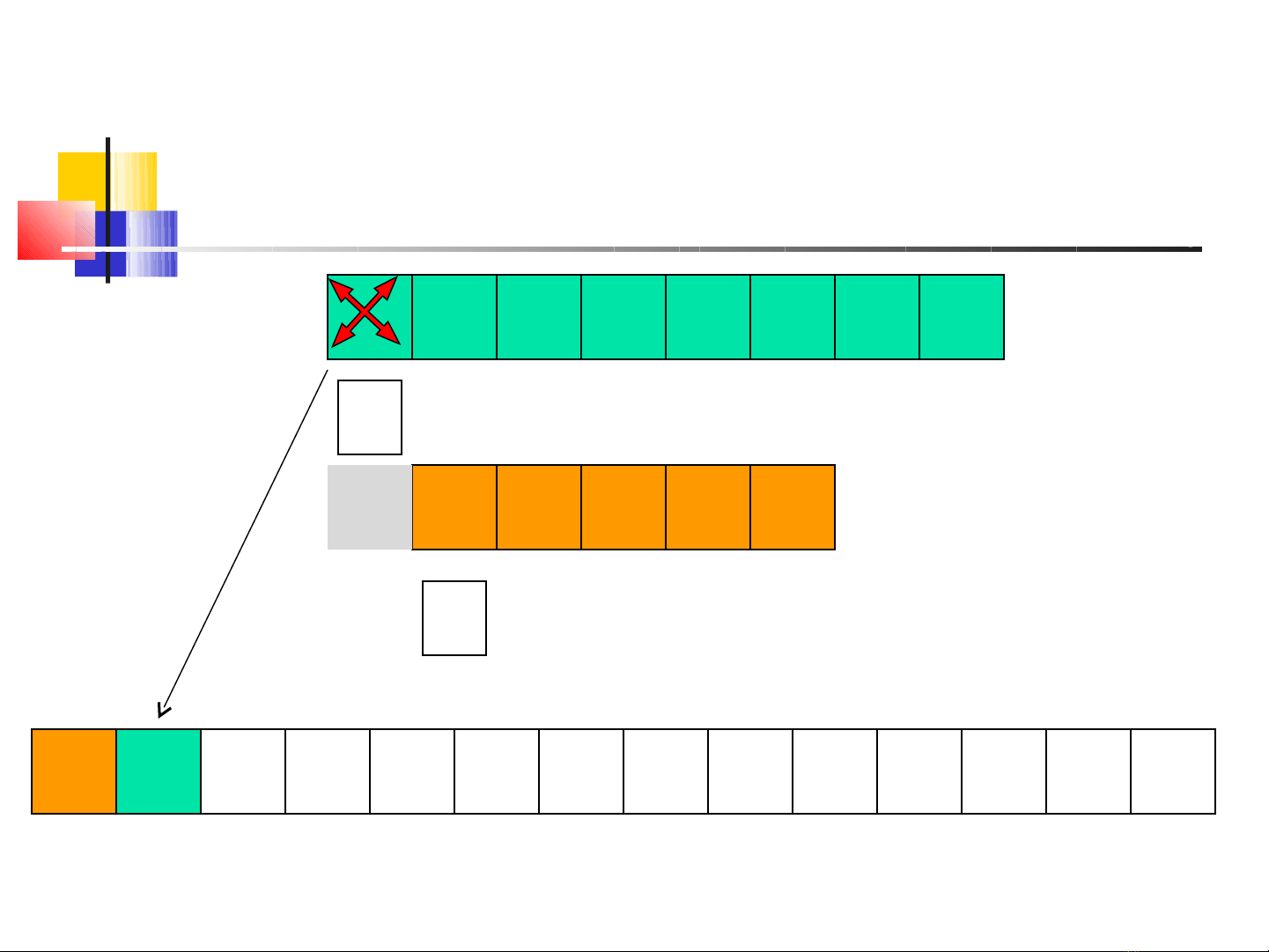
2 5 7 8 9 10 13 14
4 6 11 203
i=0
1
j=1
2
1