2009
dc e
Thiếtkếmạch sốdùng HDL
Thiết
kế
mạch
số
dùng
HDL
Chương 2: Thiết kế mạch luận lý tổ hợp
0
09
Nội dung chính
n
g 2
0
•Luận lý tổ hợp và đại số Boole
•
Qui tắctốigiảnđạisốBoole
eeri
n
•
Qui
tắc
tối
giản
đại
số
Boole
•Biểu diễn mạch luận lý tổ hợp
ể
E
ngin
•Đơn giản hóa bi
ể
u thức Boole
• Glitch và Hazard
ter
E
•Các khối cơ bản cho thiết kế luận lý
o
mpuC
o
©2009, Pham Quoc Cuong 2
Advanced Digital Design with the Verilog HDL –
cha
p
ter 2
0
09
Nội dung chính
n
g 2
0
•Luận lý tổ hợp và đại số Boole
•
Qui tắctốigiảnđạisốBoole
eeri
n
•
Qui
tắc
tối
giản
đại
số
Boole
•Biểu diễn mạch luận lý tổ hợp
ể
E
ngin
•Đơn giản hóa bi
ể
u thức Boole
• Glitch và Hazard
ter
E
•Các khối cơ bản cho thiết kế luận lý
o
mpuC
o
©2009, Pham Quoc Cuong 3
Advanced Digital Design with the Verilog HDL –
cha
p
ter 2
0
09
Mạch tổ hợp – mạch tuần tự
n
g 2
0
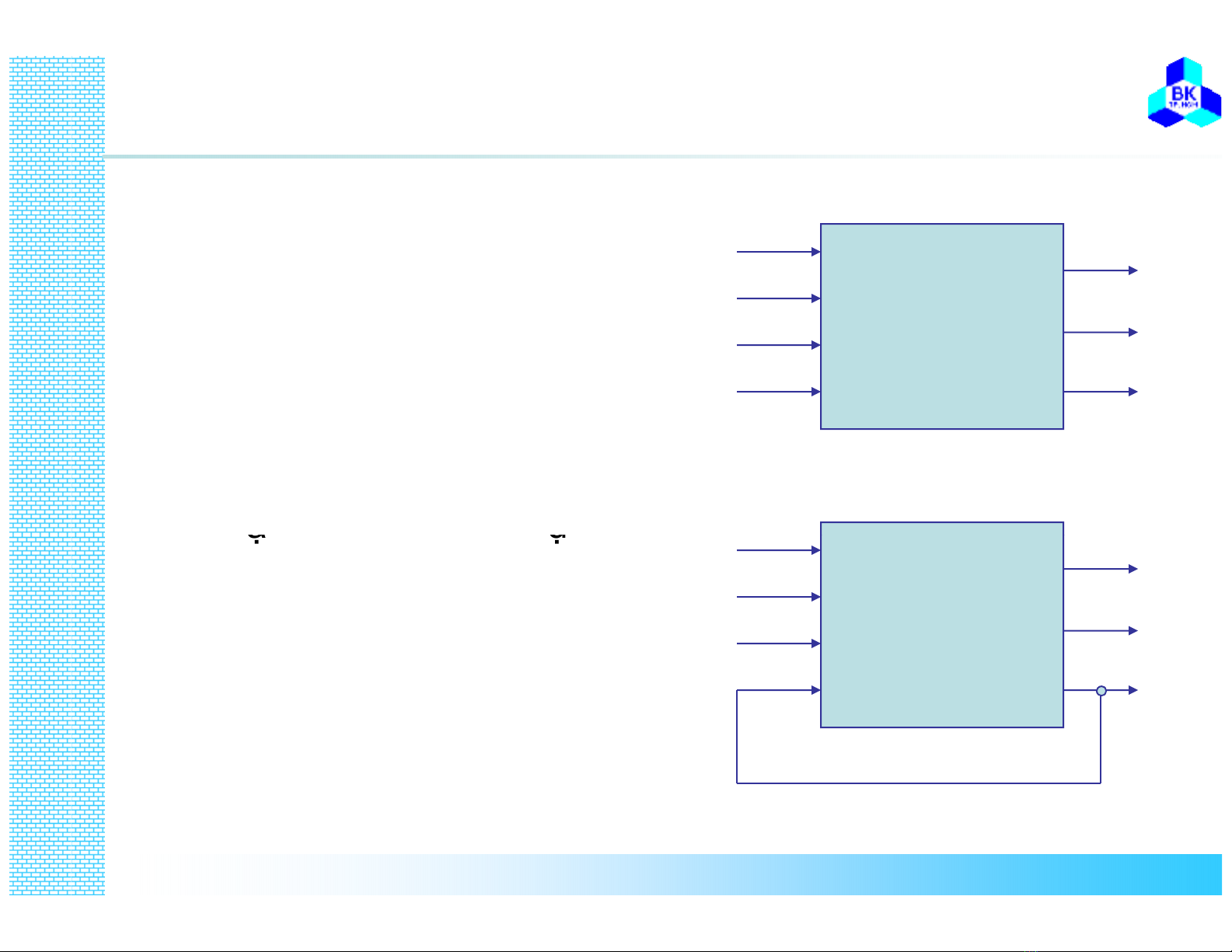
• Combinational circuit
Trạng thái ngõ ra của
Cbiti l
y1
b
a
eeri
n
mạch tại thời điểm tchỉ
phụ thuộc vào trạng thái
ngõ vào tạithờiđiểm
C
om
bi
na
ti
ona
l
Logic
c
d
y2
y3
E
ngin
ngõ
vào
tại
thời
điểm
• Sequential circuit
Trạng thái ngõ ra phụ
a
ter
E
Trạng
thái
ngõ
ra
phụ
thuộc vào “lịch sử” ngõ
ra và ngõ vào hiện tai Sequential
Circuit
y1
b
c
a
y2
o
mpu
Circuit
y3
C
o
©2009, Pham Quoc Cuong 4
Advanced Digital Design with the Verilog HDL –
cha
p
ter 2
0
09
Điện áp nguồn
n
g 2
0
• GND = 0V
•
Năm 1980 V
=5V
eeri
n
•
Năm
1980
V
DD
=
5V
•V
DD ngày càng giảm trong các bộ xử lý hiện
đại
E
ngin
đại
VDD cao làm hư các Transistor
ấ ế
ter
E
VDD th
ấ
p ti
ế
t kiệm năng lượng
•V
DD = 3.3, 2.5, 1.8, 1.5, 1.2, 1.0,…
o
mpuC
o
©2009, Pham Quoc Cuong 5
Advanced Digital Design with the Verilog HDL –
cha
p
ter 2