Ch¬ng 5 - Mét sè kiÕn thøc vÒ ®¹i sè logic
CH NG 5. M T S KI N TH C V Đ I S LOGICƯƠ Ộ Ố Ế Ứ Ề Ạ Ố
Ng i đ t n n móng cho ngành toán h c này là D. Boole (1815-1864). Do v y đ iườ ặ ề ọ ậ ạ
s logic còn có tên g i là đ i s Boole. Đ i s logic có nhi u ng d ng, đây,ố ọ ạ ố ạ ố ề ứ ụ ở
chúng ta quan tâm đ n các khía c nh liên quan đ n thi t k các m ch logic bênế ạ ế ế ế ạ
trong MTĐT. Nh đã th y, k t qu th c hi n các phép toán s h c v i các s như ấ ế ả ự ệ ố ọ ớ ố ị
phân là m t s nh phân m i. Do v y, ta có th hình dung thi t b th c hi n cácộ ố ị ớ ậ ể ế ị ự ệ
phép toán trong MTĐT nh là thành ph n ch c năng bi n đ i nh phân. Thi t bư ầ ứ ế ổ ị ế ị
đ c bi t đó cho phép n p s li u d ng nh phân đ u vào và l y k t qu cóặ ệ ạ ố ệ ạ ị ở ầ ấ ế ả
d ng nh phân đ u ra. V y có th xem b bi n đ i ch c năng đó nh là m tạ ị ở ầ ậ ể ộ ế ổ ứ ư ộ
thi t b có nhi u đ u vào và nhi u đ u ra. T i m t th i đi m xác đ nh, m i đ uế ị ề ầ ề ầ ạ ộ ờ ể ị ở ỗ ầ
vào ch n p đ c m t bit và t m i đ u ra ch cho ra đ c m t bit d li u. Đỉ ạ ượ ộ ừ ỗ ầ ỉ ượ ộ ữ ệ ể
hi u rõ h n v nguyên lý xây d ng các b bi n đ i nh phân ta s tìm hi u m tể ơ ề ự ộ ế ổ ị ẽ ể ộ
s v n đ có liên quan d i đây.ố ấ ề ướ
5.1. CÁC HÀM Đ I S LOGICẠ Ố
Xét t p D = {0, 1}, các giá tr c a t p D còn g i là giá tr logic hay nh phân. Đ iậ ị ủ ậ ọ ị ị ạ
l ng x ch có th nh n giá tr trong t p D g i là bi n Boole (hay bi n logic, bi nượ ỉ ể ậ ị ậ ọ ế ế ế
nh phân). Hàm c a n bi n nh phân F(xị ủ ế ị 1, x2, ..., xn) ch nh n hai giá tr 0 và 1 g iỉ ậ ị ọ
là hàm Boole (ho c hàm logic). M i hàm boole n bi n có th cho b ng m t b ngặ ỗ ế ể ằ ộ ả
có n+1 c t, n c t đ u là giá tr c a các bi n xộ ộ ầ ị ủ ế 1, x2, ..., xn t ng ng. C t cu i cùngươ ứ ộ ố
là giá tr c a hàm ng v i các giá tr c a bi n. Ví d n = 2, các giá tr x1, x2 vàị ủ ứ ớ ị ủ ế ụ ị
các hàm t ng ng f(x1, x2) đ c cho nh trong B ng 5.1ươ ứ ượ ư ả
x1x 2 f(x1,x2)
0 0 1
0 1 0
1 0 0
1 1 1
B ng 5.1. Hàm logic 2 bi nả ế
D dàng th y, v i m i n có đúng 2ễ ấ ớ ỗ n cách t h p khác nhau giá tr các bi n xổ ợ ị ế 1,
x2, ..., xn. M t hàm ộBoole là m t cách cho t ng ng m i m t trong s 2ộ ươ ứ ỗ ộ ố n v i m tớ ộ
trong hai giá tr 0 và 1. Vì th nó s t ng ng v i m t cách phân ho ch t p 2ị ế ẽ ươ ứ ớ ộ ạ ậ n bộ
giá tr này thành 2 nhóm, m t nhóm hàm có giá tr 1, m t nhóm hàm có giá tr 0.ị ộ ị ộ ị
Nh v y m i hàm boole n bi n hoàn toàn đ c xác đ nh b i m t t p con trong 2ư ậ ọ ế ượ ị ở ộ ậ n
b giá tr đ giá tr c a hàm là 1. Ta đã bi t đ i v i m t t p có k ph n t thì t pộ ị ể ị ủ ế ố ớ ộ ậ ầ ử ậ
t t c các t p con c a nó s có 2ấ ả ậ ủ ẽ k ph n t . Do v y có đúng 2ầ ử ậ n hàm Boole n bi n.ế
V i n = 1, có 4 hàm nh phân. Các hàm đó đ c cho trong B ng 5.2ớ ị ượ ả
37
Ch¬ng 5 - Mét sè kiÕn thøc vÒ ®¹i sè logic
x F1 F2 F3 F4
0 0 1 0 1
1 0 1 1 0
B ng 5.2. Các hàm logic 1 bi nả ế
Hàm F1 và F2 là hàm h ng (không ph thu c vào đ i s x):ằ ụ ộ ố ố
F1(x) ≡ 0 là hàm h ng 0ằ
F2(x) ≡ 1 là hàm h ng 1ằ
Giá tr F3(x) luôn b ng giá tr bi n x, đó là hàm đ ng nh t:ị ằ ị ế ồ ấ
F3(x) ≡ x
Hàm F4(x) luôn có giá tr ng c l i v i giá tr bi n x mà ta g i là hàm ph đ nh vàị ượ ạ ớ ị ế ọ ủ ị
ký hi u ệ x. D th y ễ ấ x = x
D u ấ có th xem là d u phép toán m t ngôi, cho phép t giá tr x xác đ nh giá trể ấ ộ ừ ị ị ị
x. Phép toán đó cũng có tên là phép ph đ nh (m t s tài li u dùng d u - trênủ ị ộ ố ệ ấ
đ u đ i t ng b ph đ nh thay cho d u ầ ố ượ ị ủ ị ấ đ ng tr c đ i t ng).ứ ướ ố ượ
V i n = 2, có 16 hàm logic. Giá tr c a các hàm đ c cho b ng 5.3.ớ ị ủ ượ ở ả
x y
F1
F 2
F3
F4
F5
F6
F7
F8
F9
F10
F11
F12
F13
F14
F15
F16
000000000011111111
010000111100001111
100011001100110011
110101010101010101
B ng 5.3. 16 hàm logic 2 bi nả ế
Ta xét m t vài hàm quan tr ng:ộ ọ
•F2(x, y) có giá tr 1 khi và ch khi x, y đ ng th i có giá tr 1. Hàm này đ cị ỉ ồ ờ ị ượ
kí hi u là (xệ∧y) và g i là phép nhân logic hay phép h i. ọ ộ
•F7(x, y) có giá tr 1 khi và ch khi x, y có giá tr khác nhau. Hàm này chính làị ỉ ị
ch s hàng đ n v khi c ng s h c x v i y. Vì v y F7 còn g i là phépữ ố ơ ị ộ ố ọ ớ ậ ọ
c ng theo module 2.ộ
•F8(x,y) có giá tr 0 khi và ch khi x, y đ ng th i có giá tr 0. Hàm F8(x,y)ị ỉ ồ ờ ị
đ c kí hi u (x ượ ệ ∨ y) và còn g i là phép c ng logic hay phép tuy n.ọ ộ ể
38

Ch¬ng 5 - Mét sè kiÕn thøc vÒ ®¹i sè logic
•F10(x,y) có giá tr 1 khi và ch khi x, y có cùng giá tr nh nhau, ho c 0ị ỉ ị ư ặ
ho c 1. Hàm F10(x,y) có kí hi u (x ặ ệ ∼y) và còn g i là phép t ng đ ngọ ươ ươ
•F14(x,y) có giá tr 0 khi và ch khi x có giá tr 1 đ ng th i y có giá tr 0. Hàmị ỉ ị ồ ờ ị
F14(x,y) đ c kí hi u (x ượ ệ ⇒y) và còn g i là phép kéo theo.ọ
Bài đ c thêm: Logic m nh đọ ệ ề
L n đ u tiên logic m nh đ đ c đ c p đ n trong m t bài báo c a Boole có tên là "Các quy lu tầ ầ ệ ề ượ ề ậ ế ộ ủ ậ
c a ý nghĩ". Theo đó m i m nh đ là m t kh ng đ nh. M nh đ s nh n giá tr chân lý là "đúng"ủ ỗ ệ ề ộ ẳ ị ệ ề ẽ ậ ị
hay "sai" tuỳ thu c vào kh ng đ nh có phù h p v i th c t hay không. Sau đó Boole đ a ra cácộ ẳ ị ợ ớ ự ế ư
phép toán đ tính giá tr chân lý c a nh ng m nh đ ph c t p. ể ị ủ ữ ệ ề ứ ạ
Gi s P và Q là hai m nh đ nào đó. M nh đ "P và Q" s nh n giá tr là đúng n u c P và Qả ử ệ ề ệ ề ẽ ậ ị ế ả
đ u đúng. N u th hi n giá tr đúng b ng 1 và giá tr sai là 0 ta th y giá tr chân lý c a m nh đề ế ể ệ ị ằ ị ấ ị ủ ệ ề
"P và Q" chính là phép nhân logic các giá tr chân lý c a P và Q. Do v y trong ngôn ng Tin h cị ủ ậ ữ ọ
ng i ta g i luôn phép nhân logic là phép "AND".ườ ọ
Giá tr chân lý c a m nh đ "P ho c Q" chính là phép c ng logic các giá tr chân lý c a P và Q. "Pị ủ ệ ề ặ ộ ị ủ
ho c Q" s đúng ch c n ít nh t P ho c Q đúng. Trong trong ngôn ng Tin h c, ng i ta cũng g iặ ẽ ỉ ầ ấ ặ ữ ọ ườ ọ
phép c ng logic là phép "OR".ộ
Giá tr chân lý c a m nh đ "Không ph i P" s đúng n u P sai và ng c l i. Giá tr này có th tínhị ủ ệ ề ả ẽ ế ượ ạ ị ể
b ng phép ph đ nh logic giá tr chân lý c a P. Trong trong m t s ngôn ng Tin h c, phép phằ ủ ị ị ủ ộ ố ữ ọ ủ
đ nh logic còn có m t tên g i khác là phép "NOT".ị ộ ọ
Phép c ng theo module 2 còn g i là phép "ho c lo i tr " (OR Exclusive) và trong ngôn ng tin h cộ ọ ặ ạ ừ ữ ọ
ng i ta g i nó là phép "XOR".ườ ọ
5.2. BI U DI N CÁC HÀM Đ I S LOGICỄ Ễ Ạ Ố
M t hàm đ i s logic cũng có th đ c xác đ nh thông qua các hàm đ i s logicộ ạ ố ể ượ ị ạ ố
khác, ví d hàm F7(x,y) trong B ng 5.3 có th cho b ng công th c sau:ụ ả ể ằ ứ
( x ∧ y ) ∨ ( x ∧ y )
Hai công th c d i đây g i là công th c đ i ng u De Morgan.ứ ướ ọ ứ ố ẫ
(x ∧ y) =( x) ∨ ( y), ( x V y) = ( x) ∧ ( y)
Các công th c này cho th y có th bi u di n phép c ng qua phép nhân và phépứ ấ ể ể ễ ộ
ph đ nh (và ng c l i), ch ng h n, x V y = ủ ị ượ ạ ẳ ạ ( x) ∧ ( y).
Sau đây là hai công th c khácứ :
(x ⇒ y) = x ∨ y, ( x ∼ y) = (x ∨ y) ∧ (y ∨ x).
Có nhi u cách ch ng minh m t đ ng th c logic trong đó có m t cách ch ng minhề ứ ộ ẳ ứ ộ ứ
r t đ n gi n là so sánh giá tr c a hai v v i t t c các b đ i s c th . Vì ch cóấ ơ ả ị ủ ế ớ ấ ả ộ ố ố ụ ể ỉ
m t s h u h n các b đ i s nên chúng ta có th k ra t t c các tr ng h pộ ố ữ ạ ộ ố ố ể ể ấ ả ườ ợ
trong m t b ng giá tr . Ch ng h n đ ch ng minh công th c c a hàm F7 nói trênộ ả ị ẳ ạ ể ứ ứ ủ
ta có th l p m t b ng và so sánh giá tr c a hai v ng v i m i b giá tr c a cácể ậ ộ ả ị ủ ế ứ ớ ỗ ộ ị ủ
đ i nh B ng 5.4:ố ư ả
39
Ch¬ng 5 - Mét sè kiÕn thøc vÒ ®¹i sè logic
x y x ∧ y x ∧ y ( x ∧ y) ∨ (x ∧ y) F7(x,y)
0 0 0 0 0 0
0 1 0 1 1 1
1 0 0 1 1 1
1 1 0 0 0 0
B ng 5.4. Giá tr F7(x,y)ả ị
Qua các ví d trên ta th y r ng các hàm đ i s logic này có th bi u di n qua cácụ ấ ằ ạ ố ể ể ễ
hàm đ i s logic khác.ạ ố
M t t p h p h u h n các hàm đ i s logic đ c g i là m t h hàm đ n u m iộ ậ ợ ữ ạ ạ ố ượ ọ ộ ệ ủ ế ọ
hàm đ i s lôgic khác đ u có th bi u di n đ c qua h hàm này. Có th ch ngạ ố ề ể ể ễ ượ ệ ể ứ
minh không khó khăn l m r ng h hai hàm ph đ nh và c ng logic là h hàm đ .ắ ằ ệ ủ ị ộ ệ ủ
Do công th c đ i ng u De Morgan ta th y h hai hàm ph đ nh và nhân logicứ ố ẫ ấ ệ ủ ị
cũng là h hàm đ .ệ ủ
5.3. ÁP D NG Đ I S LOGIC TRONG VI C THI T K CÁC M CHỤ Ạ Ố Ệ Ế Ế Ạ
LOGIC
MTĐT bi u di n thông tin b ng các tr ng thái c a các thành ph n v t lý. Thôngể ễ ằ ạ ủ ầ ậ
th ng các thành ph n này có hai tr ng thái đ i l p. Ví d nh m t m ch đi nườ ầ ạ ố ậ ụ ư ộ ạ ệ
đóng ho c m , chi u c a t tr ng m t vùng v t li u t nhi m t theo chi u nàyặ ở ề ủ ừ ườ ộ ậ ệ ừ ễ ừ ề
ho c chi u kia... N u dùng tr ng thái này ch giá tr 1 và tr ng thái kia ch giá tr 0ặ ề ế ạ ỉ ị ạ ỉ ị
thì ta th y r ng MTĐT là m t máy làm vi c trên h nh phân. M i phép x lý máyấ ằ ộ ệ ệ ị ọ ử
có th th c hi n đ c th c ch t là các hàm đ i s logic. Các h v t lí th c hi nể ự ệ ượ ự ấ ạ ố ệ ậ ự ệ
các hàm đ i s logic g i là các m ch logic.ạ ố ọ ạ
Ta minh h a m t s m ch logic đ n gi n dùng các công t c ng t ho c đóngọ ộ ố ạ ơ ả ắ ắ ặ
m ch có đi u khi n (g i là các r le) v i quy c r ng tr ng thái có đi n th hi nạ ề ể ọ ơ ớ ướ ằ ạ ệ ể ệ
giá tr logic 1, tr ng thái không có đi n th hi n giá tr logic 0.ị ạ ệ ể ệ ị
Ph n t ANDầ ử
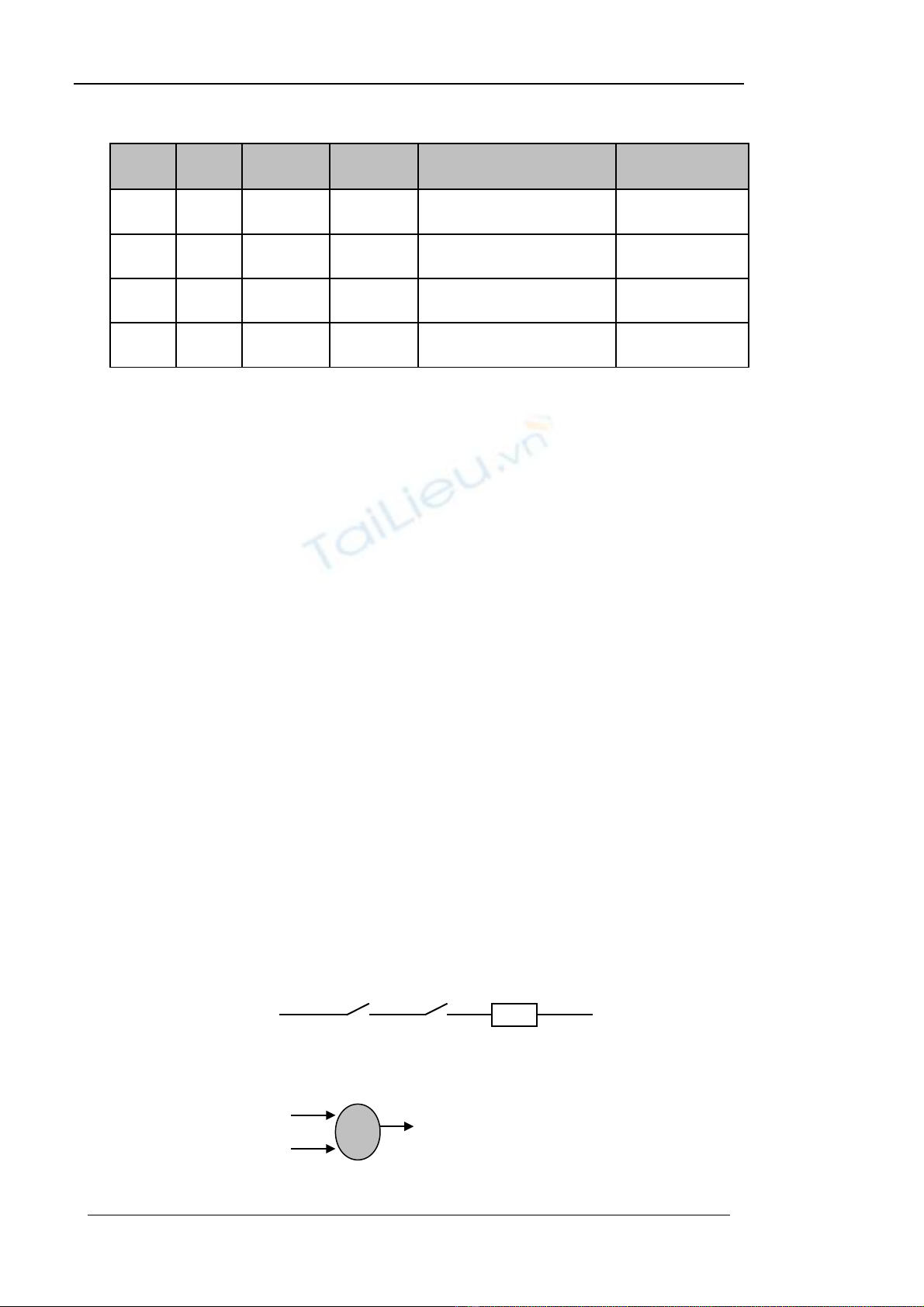
Cho m ch đi n có hai r le K1, K2 m c n i ti p nh Hình 5.1. Ch khi có dòngạ ệ ơ ắ ố ế ư ỉ
đi n đi u khi n đ đóng K1 và K2 thì m i có dòng đi n qua R. Vì v y s phệ ề ể ể ớ ệ ậ ự ụ
thu c tr ng thái R vào các tr ng thái K1, K2 có th bi n đ i R= K1ộ ạ ạ ể ế ổ ∧K2
Hình 5.1. S đ ph n t ANDơ ồ ầ ử
40
R
K1 K2
Ch¬ng 5 - Mét sè kiÕn thøc vÒ ®¹i sè logic
Ph n t ORầ ử
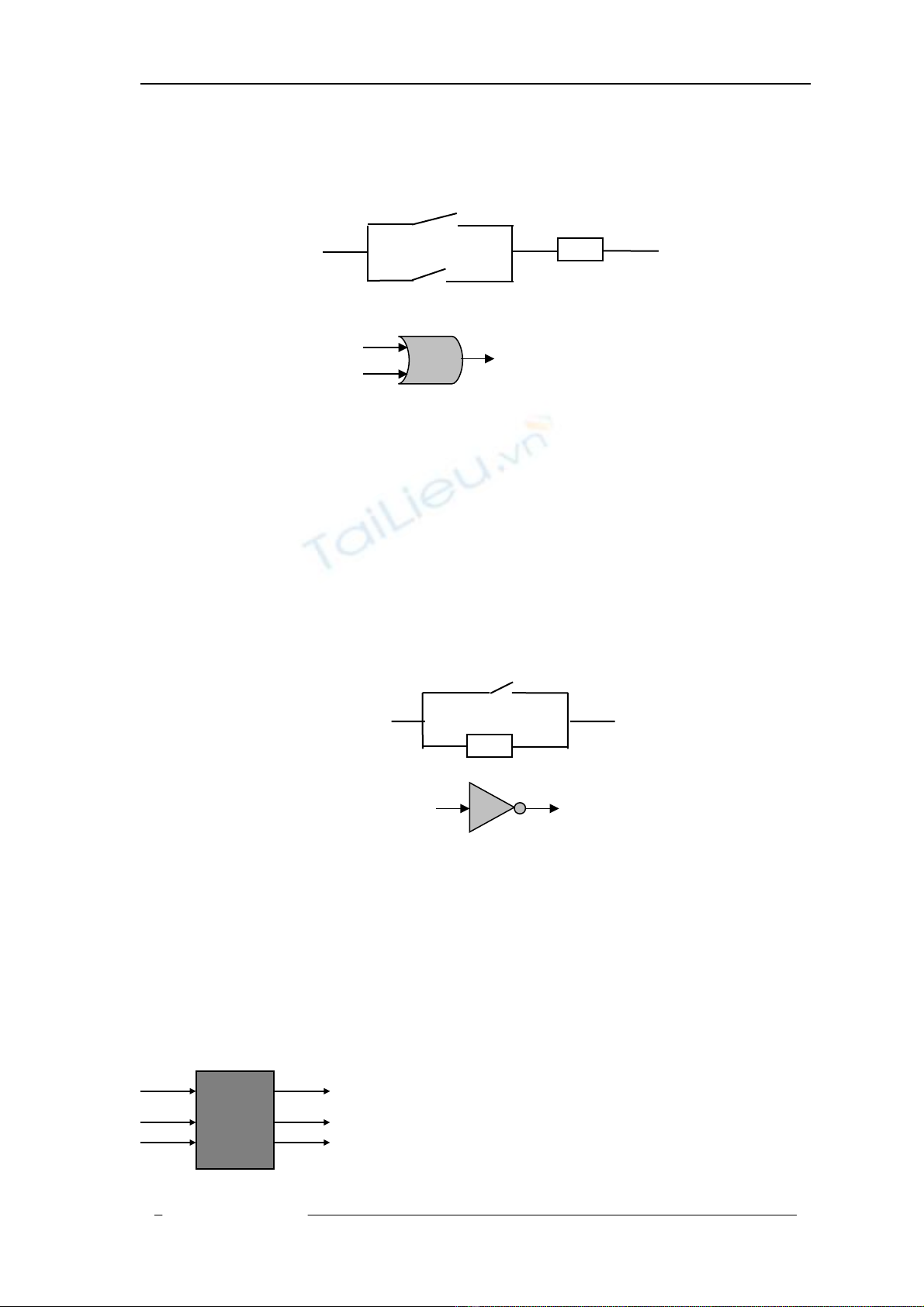
Cho m ch đi n cũng có hai r le K1, K2 v i tính ch t nh v a xét, nh ng đ cạ ệ ơ ớ ấ ư ừ ư ượ
m c song song theo Hình 5.2:ắ
Hình 5.2. S đ ph n t ORơ ồ ầ ử
D nh n th y R không có dòng đi n (th hi n giá tr 0) khi và ch khi K1 và K2ễ ậ ấ ệ ể ệ ị ỉ
đ ng th i ng t m ch (th hi n giá tr 0). Do đó, giá tr logic R th hi n là t ngồ ờ ắ ạ ể ệ ị ị ể ệ ổ
logic c a các giá tr c a K1 và K2 th hi n.ủ ị ủ ể ệ
Ph n t NOTầ ử
Xét m ch đi n có s đ nh trên Hình 5.3. Khi K m , dòng đi n ph i đi qua R,ạ ệ ơ ồ ư ở ệ ả
còn khi K đóng, do đi n tr c a K vô cùng bé so v i R nên dòng đi n đi qua K màệ ở ủ ớ ệ
không đi qua R. Do v y, giá tr logic R th hi n là ph đ nh giá tr mà K th hi n.ậ ị ể ệ ủ ị ị ể ệ
Hình 5.3. S đ ph n t NOTơ ồ ầ ử
Trên th c t các m ch logic th ng đ c ch t o t các m ch bán d n ho c cácự ế ạ ườ ượ ế ạ ừ ạ ẫ ặ
m ch vi đi n t v i kích th c siêu nh . Ng i ta cũng ch t o nh ng m chạ ệ ử ớ ướ ỏ ườ ế ạ ữ ạ
(ph n t ) OR, AND, NOT, NAND (NOT AND), NOR (NOT OR), XOR và c nh ngầ ử ả ữ
m ch có ch c năng ph c t p th c hi n các x lý ph c t p h n. Các h này g i làạ ứ ứ ạ ự ệ ử ứ ạ ơ ệ ọ
các h logic. Nh v y có th hình dung các h logic nh nh ng h p đen (mà taệ ư ậ ể ệ ư ữ ộ
không quan tâm đ n c u trúc bên trong) có m t s đ u vào và m t s đ u ra.ế ấ ộ ố ầ ộ ố ầ
Các tín hi u đ u vào và đ u ra là các tín hi u nh phân (t ng ng v i m tệ ở ầ ầ ệ ị ươ ứ ớ ộ
trong hai tr ng thái v t lý). Ta đã bi t h hàm ph đ nh, tuy n và h i là m t hạ ậ ế ệ ủ ị ể ộ ộ ệ
hàm đ . Nh v y v m t nguyên t c có th ch ng ch tủ ư ậ ề ặ ắ ể ồ ấ
các ph n t NOT và OR và AND đ t o nên b t c m tầ ử ể ạ ấ ứ ộ
máy th c hi n các phép bi n đ i nh phân nào. Ví d sauự ệ ế ổ ị ụ
đây minh h a vi c l p m ch c ng hai bit.ọ ệ ậ ạ ộ
B c ng 2 bitộ ộ
41
R
K1
K2
R
K
O
T
Hình 5.4












![Đề thi Hệ điều hành có đáp án: Tổng hợp [năm] + [loại đề/trường]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250523/oursky06/135x160/42231768898900.jpg)













