zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Tài Liệu Phổ Thông

» Trung học phổ thông

Toán học lớp 11: Hai đường thẳng vuông góc (Phần 1) - Thầy Đặng Việt Hùng

Chia sẻ: Thành Chung | Ngày: | Loại File: PDF | Số trang:5

Báo xấu

745
lượt xem 109
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tài liệu "Toán học lớp 11: Hai đường thẳng vuông góc (Phần 1) - Thầy Đặng Việt Hùng" tóm lược nội dung cần thiết và cung cấp 1 số bài tập ví dụ hữu ích, giúp các bạn củng cố và nắm kiến thức về hai đường thẳng vuông góc thật hiệu quả.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Toán học lớp 11: Hai đường thẳng vuông góc (Phần 1) - Thầy Đặng Việt Hùng

Khóa học Toán Cơ bản và Nâng cao 11 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95 02. HAI ĐƯỜNG THẲNG VUÔNG GÓC – P1 Thầy Đặng Việt Hùng [ĐVH] I. TÍCH VÔ HƯỚNG CỦA HAI VÉC TƠ TRONG KHÔNG GIAN 1) Góc giữa hai véc tơ  AB = u ( ) ( ) Giả sử ta có   → u; v = AB; AC = BAC , với 0o ≤ BAC ≤ 180o.  AC = v 2) Tích vô hướng của hai véc tơ  AB = u ( ) Giả sử ta có   → u.v = AB. AC = AB . AC .cos AB. 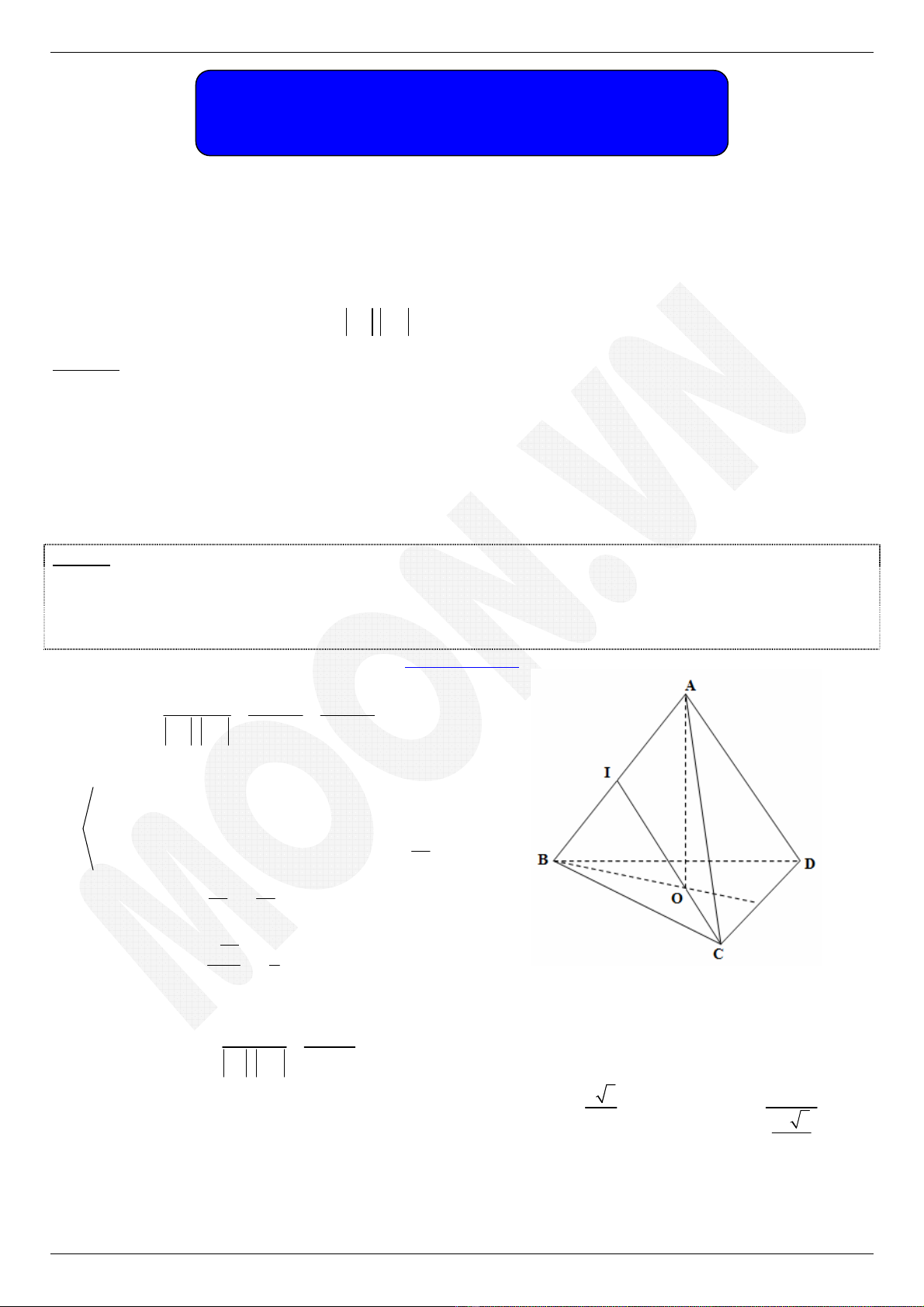AC  AC = v Nhận xét: u = 0 + Khi   → u.v = 0 v = 0 ( ) + Khi u ↑↑ v  → u ; v = 00 ( ) + Khi u ↑↓ v  → u; v = 1800 + Khi u ⊥ v ←→ u.v = 0 Ví dụ 1. Cho tứ diện đều ABCD cạnh a. ( ) a) Tính góc giữa hai véc tơ AB; BC . ( ) b) Gọi I là trung điểm của AB. Tính góc giữa hai véc tơ CI ; AC . Hướng dẫn giải: a) Sử dụng công thức tính góc giữa hai véc tơ ta được ( ) AB. BC AB. BC AB. BC cos AB; BC = = = , (1) . AB . BC AB.BC a2 ( ) Xét AB. BC = AB. BA + AC = AB.BA + AB. AC ( ) AB.BA = AB.BA.cos AB.BA = a.a.cos1800 = −a 2 Mà ( ) a2 AB. AC = AB. AC.cos AB. AC = a.a.cos 600 = 2 a 2 a 2  → AB. BC = −a 2 + =− . 2 2 2 a − ( ) ( ) 1 (1) ⇔ cos AB; BC = 22 = −  → AB; BC = 1200. a 2 ( ) Vậy AB; BC = 120 . o ( ) CI . AC CI . AC b) Ta có cos CI ; AC = = CI . AC CI . AC ( ) a 3 CI . AC Tứ diện ABCD đều cạnh a, CI là trung tuyến của tam giác đều ABC nên CI =  → cos CI ; AC = 2 , ( 2). 2 a 3 2 ( ) Ta có CI . AC = CI . AI + IC = CI . AI + CI . IC Do ∆ABC đều nên CI ⊥ AI ⇔ CI . AI = 0. Tham gia khóa Toán Cơ bản và Nâng cao 11 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
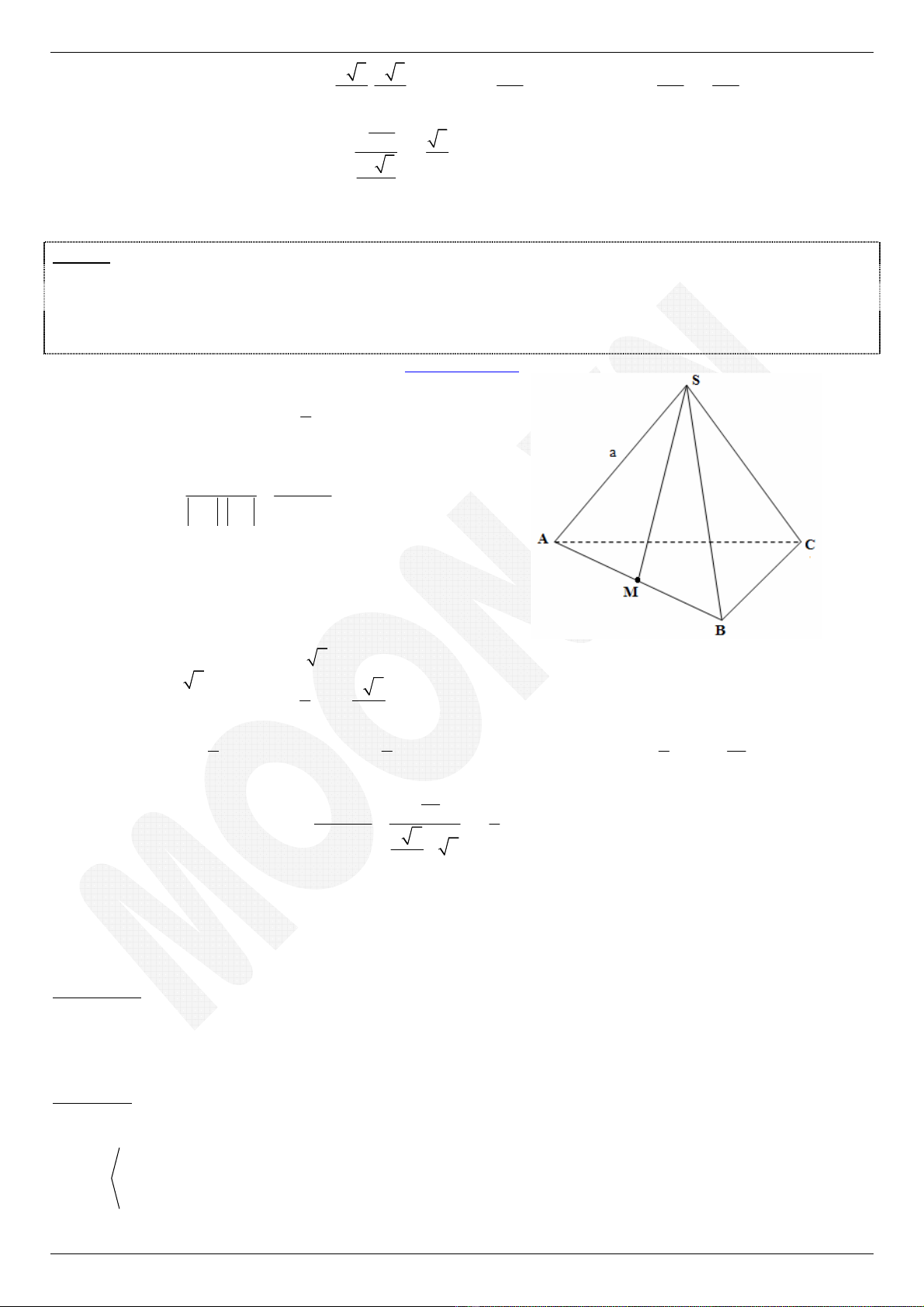
Khóa học Toán Cơ bản và Nâng cao 11 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95 ( ) a 3 a 3 3a 2 3a 2 3a 2 Đồng thời, CI . IC = CI . IC .cos CI ; IC = . .cos1800 = −  → CI . AC = 0 − =− . 2 2 4 4 4 3a 2 − ( Thay vào (2) ta được ( 2 ) ⇔ cos CI ; AC = 2 4 = − a 3 ) 2 3  ( → CI ; AC = 1500. ) 2 ( ) Vậy CI ; AC = 150 . 0 Ví dụ 2. Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA = SB = SC = a. Gọi M là trung điểm của AB. a) Biểu diễn các véc tơ SM và BC theo các véc tơ SA; SB; SC . ( ) b) Tính góc SM ; BC . Hướng dẫn giải: a) Sử dụng quy tắc trung tuyến và quy tắc trừ hai véc tơ ta  1 ( )  SA + SB = 2SM  SM = SA + SB được  ← → 2  BC = BS + SC  BC = SC − SB  ( ) SM . BC SM . BC b) cos SM ; BC = = , (1) . SM . BC SM .BC  SA.SB = 0  Mà SA, SB, SC đôi một vuông góc nên  SA.SC = 0   SB.SC = 0 Tam giác SAB và SBC vuông tại S nên theo định lý Pitago ta  BC = a 2  được AB = BC = a 2  → 1 a 2  SM = AB =  2 2 1 1   2 ( Theo câu a, SM .BC = SA + SB . SC − SB =  )( ) SA 2  0 .SC − SA.SB + SB. SC − SB .SB  = − 1 2 2 SB = − a2 2 0 0  a2 SM . BC − ( Thay vào (1) ta được cos SM ; BC = ) SM .BC a 2 = 2 1 = −  2 ( ) → SM ; BC = 1200. .a 2 2 II. GÓC GIỮA HAI ĐƯỜNG THẲNG 1) Khái niệm véc tơ chỉ phương của đường thẳng Một véc tơ u ≠ 0 mà có phương song song hoặc trùng với d được gọi là véc tơ chỉ phương của đường thẳng d. 2) Góc giữa hai đường thẳng Khái niệm: Góc giữa hai đường thẳng a và b là góc giữa hai đường thẳng a′; b′ lần lượt song song với a; b. Kí hiệu ( a;b ). a// a ′ Từ định nghĩa ta có sơ đồ  → (  a;b ) = ( a ′;b′ )  b// b ′ Nhận xét: ( ) + Giả sử a, b có véc tơ chỉ phương tương ứng là u; v và u; v = φ. ( a; b ) = φ ; 0o ≤ φ ≤ 90o Khi đó, ( a; b ) = 180o − φ ; 90o < φ ≤ 180o + Nếu a // b hoặc a ≡ b thì ( a; b ) = 0o. Tham gia khóa Toán Cơ bản và Nâng cao 11 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
Khóa học Toán Cơ bản và Nâng cao 11 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95 Các xác định góc giữa hai đường thẳng: Phương án 1 Phương án 2 (sử dụng định nghĩa) a ′// a Tạo ra các đường  → (  a, b ) = ( a ′, b′ ) - Lấy một điểm O bất kì thuộc a  b ′ // b → ( - Qua O, dựng đường ∆ // b  a, b ) = ( a, ∆ ) Chú ý: Các phương pháp tính toán góc giữa hai đường thẳng: Nếu góc thuộc tam giác vuông thì dùng các công thức tính toán trong tam giác vuông: sin, cosin, tan, cot. Nếu góc thuộc tam giác thường thì sử dụng định lý hàm số cosin trong tam giác ABC: b2 + c 2 − a 2 a 2 = b 2 + c 2 − 2bc cos A  → cos A = . 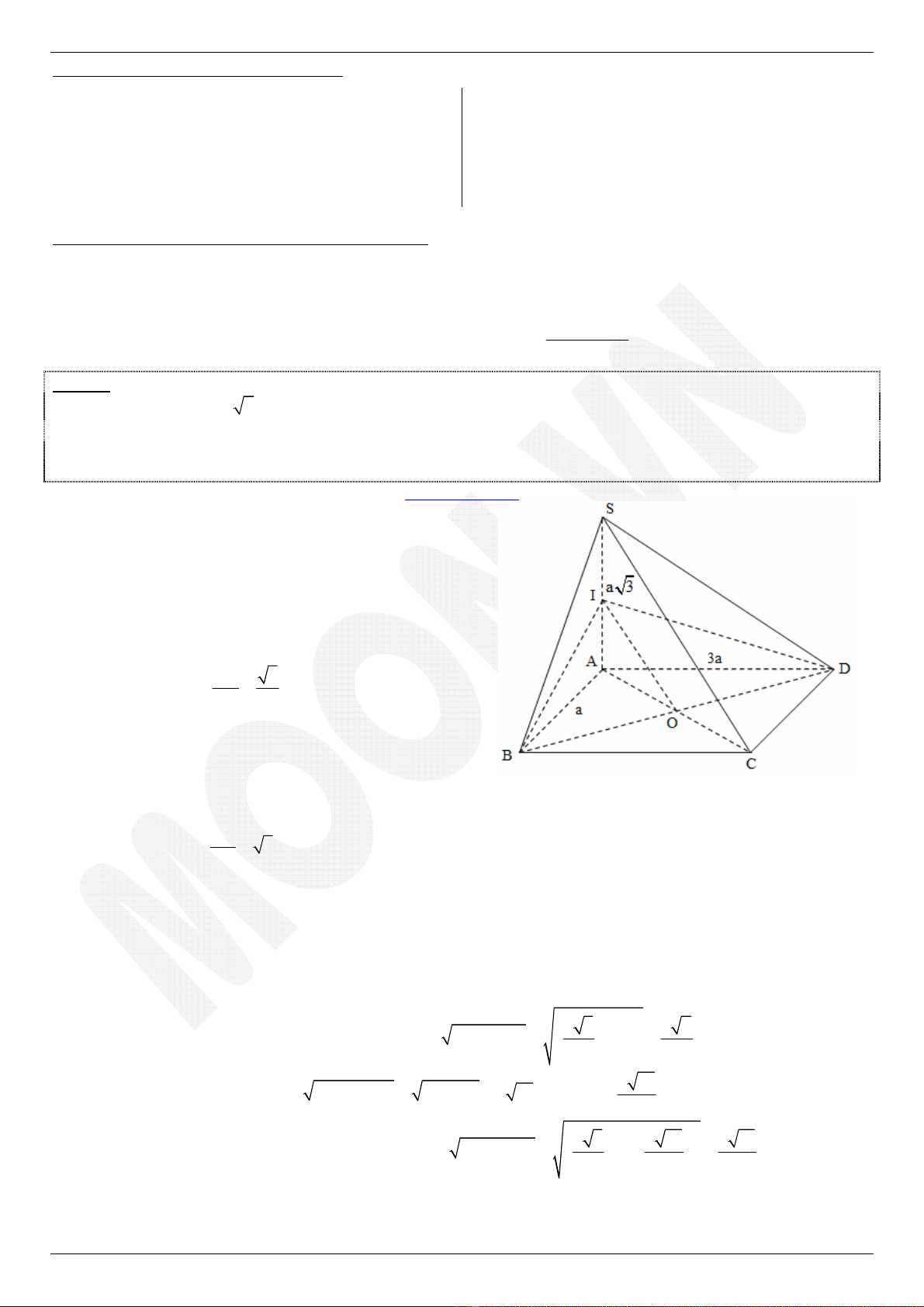2bc Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, các tam giác SAB, SAD, SAC là các tam giác vuông tại A. Biết SA = a 3; AB = a; AD = 3a . Tính góc giữa các đường thẳng sau: a) SD và BC. b) SB và CD. c) SC và BD. Hướng dẫn giải: a) Tính góc giữa SD và BC Để xác định góc giữa hai đường thẳng SD và BC ta sử dụng phương án 2, tìm đường thẳng song song với một trong hai đường thẳng SD, BC và song song với một đường còn lại. Ta dễ nhận thấy AD // BC. SDA Khi đó (SD; BC ) = ( SD; AD ) =  180 − SDA o = SA 3 = 30o. Xét ∆SAD: tan SDA =  → SDA AD 3 Vậy (SD; BC ) = 30o. b) Tính góc giữa SB và CD SBA → ( Tương tự, CD//AB  SB;CD ) = ( SB;AB ) =  180o − SBA = SA = 3  Xét ∆SAB: tanSBA = 60o. → SDA AB ( V ậy ) SB;CD = 60o. c) Tính góc giữa SC và BD Gọi O là tâm của hình chữ nhật ABCD, I là trung điểm của SA.  IOB Trong ∆SAC có OI // SC  → (SC; BD ) = ( OI; BD ) =  180 − IOB o 2 a 3 a 7 Áp dụng định lý Pitago cho tam giác vuông ABI: IB = IA + AB =  2  + a = 2 2  2  2 a 10 ABCD là hình chữ nhật nên BD = AB2 + AD 2 = a 2 + 9a 2 = a 10  → OB = = OA 2 2 2  a 3   a 10  a 13 Áp dụng định lý Pitago cho tam giác vuông ABO: IO = IA + AO =  2  +  2  =  2   2  2 Tham gia khóa Toán Cơ bản và Nâng cao 11 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
Khóa học Toán Cơ bản và Nâng cao 11 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95 13a 2 10a 2 7a 2 + − = OI + OB − IB = 4 2 2 2 Khi đó, theo định lý hàm số cosin cho ∆IOB ta được: cos IOB 4 4 = 8 2.OI.OB a 13 a 10 130 2. . 2 2 = arccos  8  = (  → IOB   SC;BD ).  130   8  Vậy ( SC;BD ) = arccos  .  130  Ví dụ 2. Cho tứ diện ABCD, gọi M, N là trung điểm của BC, AD. Biết AB = CD = 2a , MN = a 3 . Tính góc giữa hai đường thẳng AB và CD. Hướng dẫn giải: Do AB và CD là các cạnh của tứ diện nên chúng chéo nhau, để xác định góc giữa hai đường thẳng AB và CD ta tạo các đường thẳng tương ứng song song với AB, CD và chúng cắt nhau. Gọi P là trung điểm của AC, khi đó MP // AB, NP // CD  MPN  → ( AB,CD ) = ( MP, NP ) =  180o − MPN Do MP, NP là các đường trung bình nên ta có MP = NP = a. Áp dụng định lý hàm số cosin trong ∆MPN ta được = MP + NP − MN = 2a − 3a = − 1 2 2 2 2 2 cos MPN 2MP.NP 2.a.a 2  = 120o ⇔ ( → MPN MP, NP ) = 60o Vậy (AB,CD ) = 60o. Nhận xét: Ngoài việc khởi tạo P như trên ta cũng có thể lấy điểm P là trung điểm của BD, cách giải khi đó cũng tương tự. Ví dụ 3. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D, AD = DC = a, AB = 2a. SA vuông góc với 2 3a AB và AD, SA = . Tính góc của 2 đường thẳng 3 a) DC và SB. b) SD và BC. Hướng dẫn giải: Tham gia khóa Toán Cơ bản và Nâng cao 11 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
Khóa học Toán Cơ bản và Nâng cao 11 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95 → ( a) Do DC // AB  DC,SB ) = ( AB,SB ) = α 2a 3 SA 3 Tam giác SAB vuông tại A nên α là góc nhọn, khi đó tan α = = 3 =  → α = 30o AB 2a 3 Vậy góc giữa hai đường thẳng DC và SB bằng 30o. b) Gọi I là trung điểm của AB, khi đó AI = a. Tứ giác ADCI là hình bình hành (do AI // DC), có AI = AD = a nên là hình thoi. Lại có góc A, D vuông nên ADCI là hình vuông cạnh a  → DI = a 2. mặt khác, tứ giác BIDC là hình bình hành (do cặp cạnh DC và BI song song và bằng nhau) nên BC // DI. Khi đó, ( ) ( SD, BC = ) SD, DI = β . 2  2a 3  7a 2 Tam giác SAI vuông tại A nên SI = SA + AI =  2 2  + a = 2 2  3  3 2  2a 3  7a 2 Tam giác SAD vuông tại A nên SD = SA + AD =  2 2  + a = 2 2  3  3 = SD + DI − SI = 2 2 2 2a 2 3 Áp dụng định lý hàm số cosin trong tam giác SDI ta được cosSDI = 2SD.DI a 21 42 2. .a 2 3 > 0 nên góc SDI là góc nhọn  Do cosSDI = arccos  3  . → β = SDI    42  BÀI TẬP LUYỆN TẬP: Bài 1. [ĐVH]: Cho tứ diện đều ABCD cạnh a, gọi I là trung điểm cạnh AD. Tính góc giữa hai đường thẳng AB và CI.  3 Đ/s: ( AB; CI ) = arccos   .  6  Bài 2. [ĐVH]: Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của BC, AD và AC. Biết rằng AB = 2a, CD = 2a 2, MN = a 5. Tính góc giữa hai đường thẳng AB và CD. ( ) Bài 3. [ĐVH]: Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC = a 2. Tính góc giữa SC , AB , từ đó suy ra góc giữa SC và AB. Bài 4. [ĐVH]: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a; AD = 2a 2; SC = 3a . Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của AB. Tính góc giữa ( ) a) SB; AC b) ( SC ; AM ) , với M là trung điểm của CD. Bài 5. [ĐVH]: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B, AB = BC = a; AD = 2a; SD = 4a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc AB với AH = −3HB . Tính góc giữa ( ) a) SA; BD b) ( SB; AC ) Tham gia khóa Toán Cơ bản và Nâng cao 11 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.