Tổng hợp đề kiểm tra học kì 1 môn Toán lớp 8 năm 2010-2011

Chia sẻ: Tran Bao Toan | Ngày: | Loại File: DOC | Số trang:14

Thêm vào BST

Báo xấu

1.111
lượt xem 130
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bộ "Tổng hợp đề kiểm tra học kì 1 môn Toán lớp 8 năm 2010-2011" gồm những câu hỏi trắc nghiệm và tự luận. Tham khảo để các em nắm vững kiến thức, nâng cao tư duy và rèn luyện kỹ năng giải đề. Chúc các em ôn thi và học tập tốt!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Tổng hợp đề kiểm tra học kì 1 môn Toán lớp 8 năm 2010-2011

ĐỀ KIỂM TRA HỌC KỲ I Năm học 2010-2011 Môn : Toán - Lớp 8 Thời gian làm bài: 90 phút ĐỀ 1: I.Trắc nghiệm khách quan ( 3 điểm ) Khoanh tròn vào một chữ cái trước câu trả lời đúng Câu 1. Kết quả của phép tính 20x2y2z : 4xyz là : B. 5x2y2z A. 5xyz C. 15xy D. 5xy Câu 2. Kết quả phân tích đa thức 2x – 1 – x2 thành nhân tử là: A. (x -1)2 B. – (x -1)2 C. – (x +1)2 D. (- x -1)2 Câu 3. Giá trị của biểu thức M = - 12x y tại x = -1, y = 1 là : 23 A. 2 B. – 2 C. 12 D. – 12 x+2 x +1 Câu 4. Mẫu thức chung của hai phân thức bằng: và x − x2 2 − 4 x + 2 x2 A. 2(1 – x)2 B. x(1 – x)2 C. 2x(1- x)2 D. 2x(1 – x) x −1 x + 2 Câu 5. Kết quả của phép tính + là : x 2 2x +1 x2 + 4 x − 2 x2 + 2 x − 2 A. B. C. D. -1 + x x+2 2x 2x x2 − 2 M Câu 6. Đa thức M trong đẳng thức = là: 2x + 2 x +1 A. 2x2 – 2 B. 2x2 – 4 C. 2x2 + 2 D. 2x2 + 4 3x − 1 Câu 7. Điều kiện xác định của phân thức 2 là : 9x −1 −1 −1 1 1 A. x ≠ B. x ≠ C. x ≠ và x ≠ D. 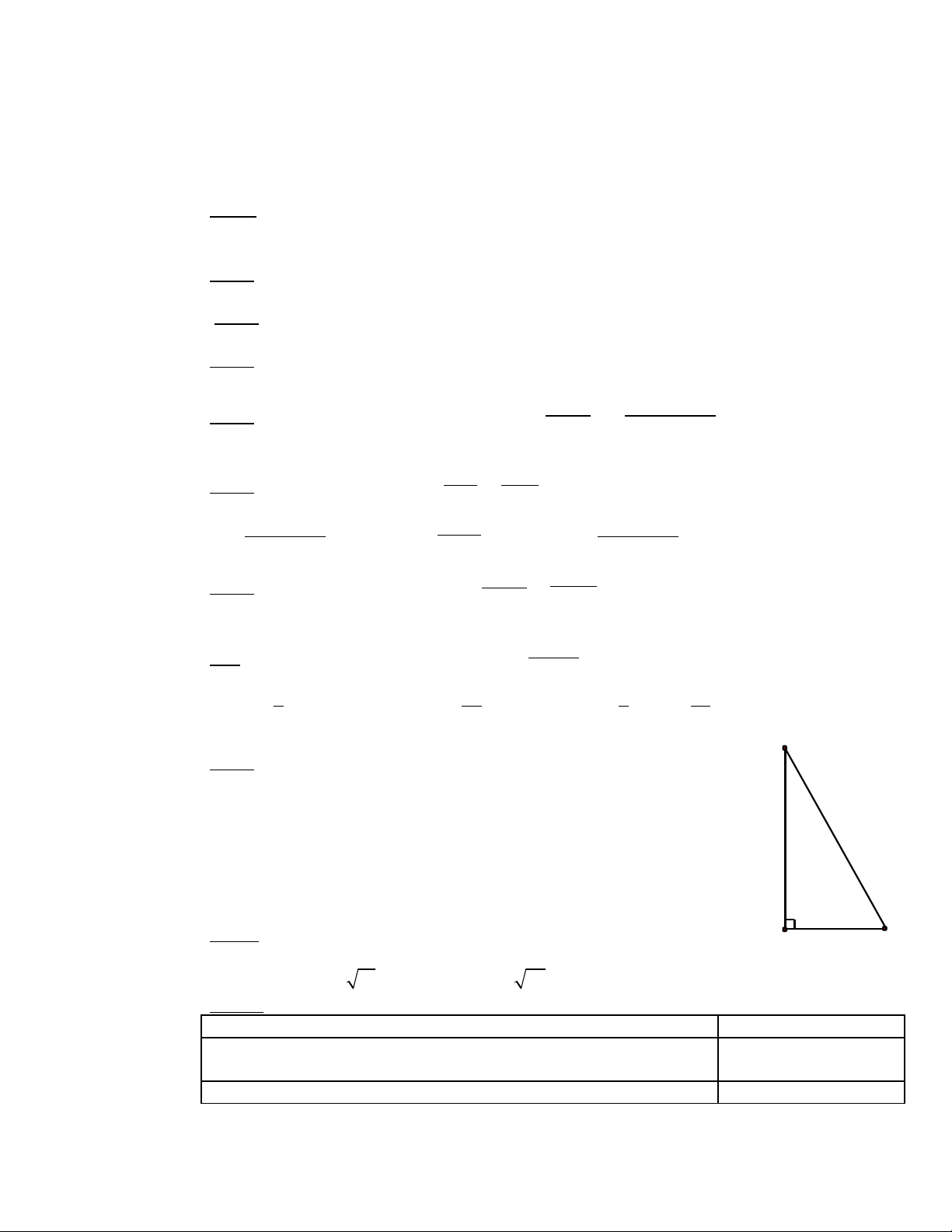x ≠ 9 3 3 3 3 B Câu 8. Cho tam giác ABC vuông tại A, AC = 3cm, BC = 5cm như hình 1. Diện tích của tam giác ABC bằng: 5cm A. 6cm2 B. 10cm2 3cm Hình 1 2 2 C. 12cm D. 15cm Câu 9. Độ dài đường chéo của một hình thoi bằng 4cm và 6cm. Độ dài cA nh của hình ạ C thoi là: A. 13cm B. 13 cm C. 52 cm D. 52cm Câu 10. Nối mỗi ý ở cột A với một ý ở cột B để được kết luận đúng. A B a) Tứ giác có hai cạnh đối song song, hai cạnh đối kia bằng nhau 1. là hình thoi và không song song b) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi 2. là hình chữ nhật
đường c) Tứ giác có hai cặp cạnh đối song song và một góc bằng 900 3. là hình bình hành 4. là hình thang cân II.TỰ LUẬN Bài 1: ( 0,75 điểm ) Phân tích đa thức thành nhân tử : a. x2 + 2x + 1 b. x2 – xy + 5x – 5y Bài 2. ( 1,25 điểm ) Thực hiện phép tính sau: 2 x + 6 x2 + 3x b) ( 4x4y2 + 6 x2y3 – 12x2y ) : 3x2y a) : 3x − x 1 − 3x 2 8 x 3 − 12 x 2 + 6 x − 1 Bài 3. ( 1,75 điểm ) Cho biểu thức P = 4 x2 − 4x + 1 a) Tìm điều kiện xác định của biểu thức P b) Rút gọn P b) Chứng minh rằng với mọi giá trị của x nguyên thì P nguyên Bài 4 : ( 2,75 điểm ) Cho ΔABC vuông ở A , trung tuyến AM . Gọi I là trung điểm của AB , N là điểm đối xứng với M qua I a. Các tứ giác ANMC , AMBN là hình gì ? Vì sao ? b. Cho AB = 4 cm ; AC = 6 cm .Tính diện tích tứ giác AMBN c. Tam giác vuông ABC có điều kiện gì thì AMBN là hình vuông ? Bài 5 : (0,5 điểm) Tìm giá trị nhỏ nhất của các biểu thức sau : 2 C= 2 x - 6x + 15 ĐỀ 2: Câu 1: (2 điểm) Thực hiện phép tính: x2 − x x − 1 + Với x ≠ 1 3x (5x2- 2x-1) a. c. x −1 1− x x 2 − 10 x + 25 x Với x ≠ 1 Với x ≠ 0, x ≠ 5 2 b. (x – 2x + 1) : (x – 1) d. : x2 − 5x x −5 Câu 2: (1,5 điểm) Rút gọn các biểu thức sau: 2( x − 5) x 2 -1 Với x ≠ 0, x ≠ 1 Với x ≠ 0, x ≠ 5 a. b. x(5 − x) x(x-1) Câu 3: (2,5 điểm) a. Phân tích đa thức thành nhân tử x2 – xy + x – y
x 2 − 10 x + 25 b. Cho đa thức P = Với x ≠ 0, x ≠ 5. Tính giá trị của P khi x = 10. x2 − 5x Câu 4: (4 điểm) Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Từ H vẽ HE và HF lần lượt vuông góc với AB và AC (E ∈ AB, F ∈ AC). a. Chứng minh AH = EF. b. Trên tia FC xác định điểm K sao cho FK = AF. Ch ứng minh t ứ giác EHKF là hình bình hành. c. Với BC = 5cm, AC = 4cm. Tính diện tích tam giác ABC. ĐỀ 3: I.Tr¾c nghiÖm (4®iÓm) khoanh trßn ch÷ c¸i tríc c©u tr¶ lêi ®óng: 1. Gi¸ trÞ x tháa m·n x 2 + 16x = 8x lµ: A. x = 8 B. x = 4 C. x = - 8 D. x = -4 2. KÕt qu¶ cña phÐp tÝnh 15x 2 y 2z : (3xyz) lµ: A. 5xyz C. 15xy D. 5xy B. 5 x 2 y 2 z 3. KÕ qu¶ cña phÐp ph©n tÝch ®a thøc 2x – 1– x2 thµnh nh©n tö lµ: A. (x – 1)2 B. - (x – 1)2 C. - (x + 1)2 D. (- x – 1)2 4. Kết quả của phép chia (x2 – 2x + 1) : (x – 1) là: C. (x + 1)2 D. (x – 1)2 A. x + 1 B. x – 1 x −1 x+2 5. KÕt qu¶ cña phÐp nh©n vµ lµ: x 2 2x + 1 x 2 + 4x + 2 x2 + x − 2 D. −x + 1 B. A. C. 2x + 2 2x 2x x2 − 2 M = 6. §a thøc M trong ®¼ng thøc lµ x + 1 2x + 2 A. 2x 2 − 2 B. 2x 2 − 4 C. 2x 2 + 2 D. 2x 2 + 4 x −9 7. §iÒu kiÖn x¸c ®Þnh cña ph©n thøc 2 1 lµ: x− 9
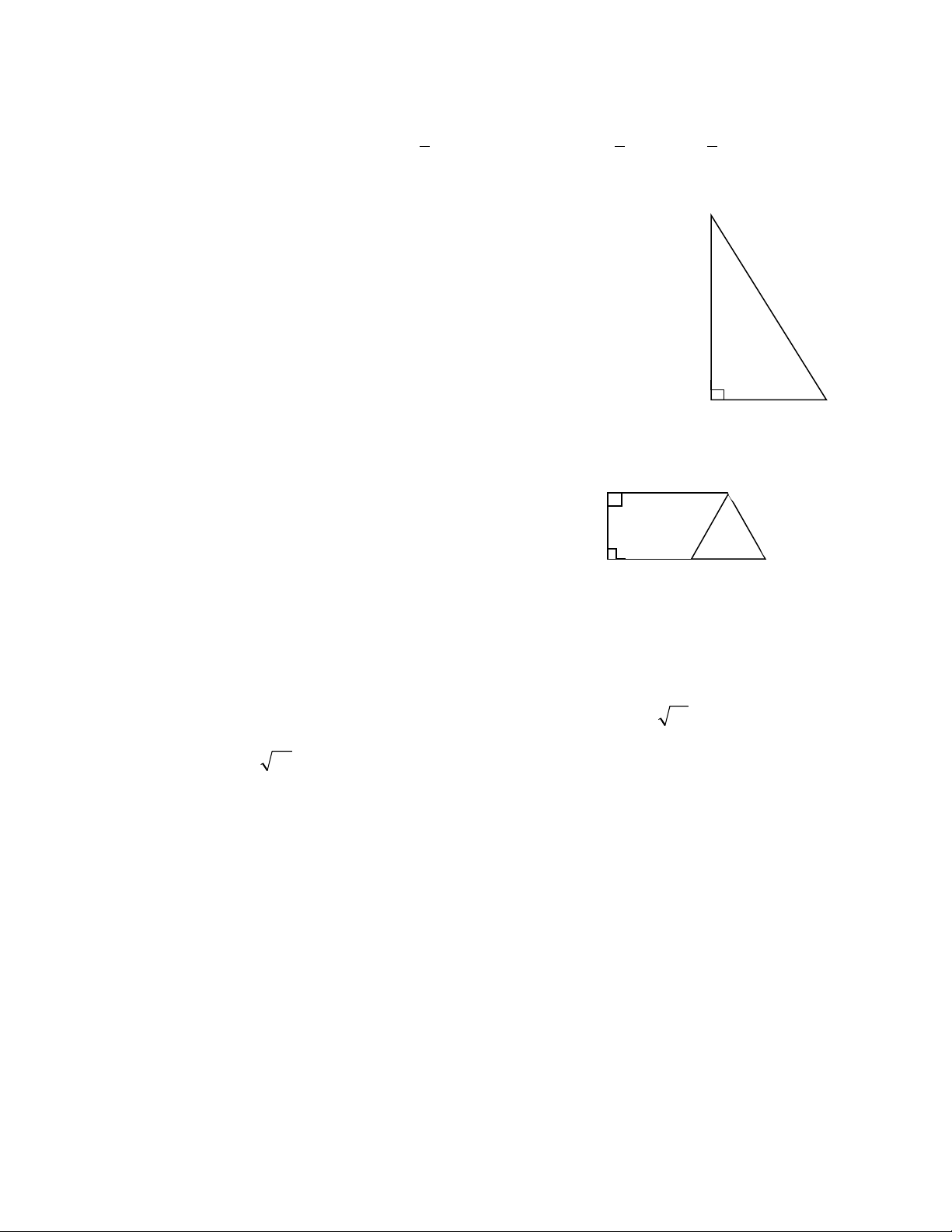
1 1 1 B. x ≠ − C. x ≠ vµ x ≠ − D. x ≠ 9 A. x ≠ −1 3 3 3 8. Cho ∆A BC vu«ng t¹i A, B AC = 3cm, BC = 5cm (h×nh 1). DiÖn tÝch cña ∆A BC b»ng: A. 6cm2 5 cm B. 10cm2 C. 12cm2 3 cm D. 15cm2 A C H× 1 nh 9. Trong h×nh 2 biÕt ABCD lµ h×nh thang vu«ng, BMC lµ tam gi¸c ®Òu. Sè ®o cña gãc ABC lµ: B A A. 600 B. 1300 C D C. 1500 M D. 1200 H×nh 2 10. §é dµi 2 ®êng chÐo cña mét h×nh thoi b»ng 4cm vµ 6cm. §é dµi c¹nh h×nh thoi lµ: A. 13cm B. 13cm C. D. 52cm 52 cm 11. Kh¼ng ®Þnh nµo sau ®©y lµ sai ? A. Tø gi¸c cã hai ®êng chÐo vu«ng gãc víi nhau t¹i trung ®iÓm cña mçi ®êng lµ h×nh thoi. B. Tø gi¸c cã hai ®êng chÐo c¾t nhau t¹i trung ®iÓm cña mçi ®êng lµ h×nh b×nh hµnh. C. H×nh ch÷ nhËt cã hai ®êng chÐo b»ng nhau lµ h×nh vu«ng. D. H×nh ch÷ nhËt cã hai ®êng chÐo vu«ng gãc víi nhau lµ h×nh vu«ng. 12. §iÒn vµo chç ( … ) nh÷ng ®a thøc thÝch hîp: a)(2x + y 2 ).(...................................) = 8x 3 + y 6 b)(27x 3 + 27x 2 + 9x + 1) : (3x + 1)2 = (................................) 13. Nèi mçi ý ë cét Avíi mét ý ë cét B ®Ó ®îc kÕt luËn ®óng.
A B a) Tø gi¸c cã hai c¹nh ®èi song song, hai c¹nh ®èi kia b»ng nhau vµ 1. lµ h×nh thoi kh«ng song song 2. lµ h×nh thang c©n b) Hình thang cã hai ®êng chÐo c¾t nhau t¹i trung ®iÓm cña mçi ®êng c) Tø gi¸c cã hai c¹nh ®èi song song vµ hai gãc ®èi b»ng 900 3. Lµ h×nh b×nh hµnh 4. lµ h×nh ch÷ nhËt II. Tù luËn ( 6 ®iÓm). Câu 1: Rút gọn phân thức 8 xy ( 3 x − 1) 9 − ( x + 5) 3 2 a) b) 2 12 x 3 (1 − 3 x ) x + 4x + 4 Câu 2: Chứng minh rằng biểu thức: n.(2n – 3) – 2n.(n +1) luôn chia hết cho 5 với mọi số nguyên n. Câu 3: Cho tam giác ABC cân tại A, đường trung tuyến AM. G ọi I là trung đi ểm c ủa AC; K là điểm đối xứng với M qua I. a) Tứ giác AMCK là hình gì ? vì sao. b) Tứ giác AKMB là hình gì ? vì sao. c) Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông ĐỀ 4: C©u 1: (1,5 ®iÓm) Ph©n tÝch c¸c ®a thøc sau thµnh nh©n tö: a) 3x2 – 9x b) x(x – 1) + 2(x – 1) c) y3 – 4y C©u 2: (2,0 ®iÓm) a) TÝnh gi¸ trÞ cña biÓu thøc (x + 1)2 + (2 – x)(2 + x) t¹i x = 200. b) Cho biÓu thøc A = 2x2 + y2 + 2xy + 2x + 1. Chøng minh r»ng biÓu thøc A lu«n nhËn gi¸ trÞ kh«ng ©m víi mäi gi¸ trÞ cña x, y. 2 1 2 −2 C©u 3: (2,0 ®iÓm) Cho biÓu thøc A =  : 2 Víi x ≠ 2 vµ x ≠ -2  x − 2 x − 4  3x − 12 a) Rót gän biÓu thøc A b) T×m x biÕt A = 3 C©u 4: (3,0 ®iÓm) Cho tam gi¸c ABC vu«ng t¹i A, AH lµ ® êng cao (H∈BC). KÎ HE, HF lÇn lît vu«ng gãc víi AB vµ AC (E∈AB, F∈AC). a) Chøng minh AH = EF b) Gäi O lµ giao ®iÓm cña AH vµ EF, K lµ trung ®iÓm cña AC. Qua F kÎ ® - êng th¼ng vu«ng gãc víi EF c¾t BC t¹i I. Chøng minh tø gi¸c AOIK lµ h×nh b×nh hµnh. c) EF c¾t IK t¹i M. Chøng minh tam gi¸c OMI c©n.
C©u 5: (1,0 ®iÓm) T×m c¸c sè nguyªn d¬ng a, b tháa m·n ab + b – a = 20 ĐỀ 5: I/ PhÇn tr¾c nghiÖm : (3 ®iÓm) Chän ®¸p ¸n phï hîp 3x − 1 1) Gi¸ trÞ cña ph©n thøc 2 ®îc x¸c ®Þnh khi: x −4 1 A. x ≠ ± 4 B. x ≠ ± 2 C. x ≠ ± D. x ≠ ± 2 2 H×nh b×nh hµnh ABCD lµ h×nh ch÷ nhËt khi 2) A. AC = BD ; B . AC ⊥ BD ; C. AC // BD ; D. AC // BD vµ AC = BD x−3 3) Ph©n thøc nghÞch ®¶o cña lµ : 2−x x−2 3− x 2−x D.Mét ®¸p ¸n kh¸c . A. ; B. ; C. ; 3− x 2−x 3− x 4) Cho tam gi¸c ABC vu«ng t¹i A, AB = 9cm , AC = 12 cm . KÎ trung tuyÕn AM. §é dµi ®o¹n th¼ng AM b»ng: A. 4,5 cm ; B. 6 cm ; C. 7,5 cm ; D. 10 cm . 6) 1− x 2 5) Ph©n thøc rót gän thµnh: x( x − 1) 1+ x 1+ x 1 2 A. B. - C. D. – x x x x 6) Hai ®êng chÐo cña h×nh thoi b»ng 6cm vµ 8cm, c¹nh cña h×nh thoi b»ng: A. 28cm ; B. 5cm ; C. 7cm ; D. 82cm . II/PhÇn tù luËn : (7 ®iÓm) Bµi 1: (2 ®iÓm) Thùc hiªn phÐp tÝnh. x−6 3 −2 a) x + 3 x + 3x 2x2 − x x + 1 2 − x2 + + b) x −1 1− x x −1 Bµi 2 : (2 ®iÓm) Cho biÓu thøc. x 1 2 x ) (Víi x ≠ ±2) A= ( 2 + – ) : (1 – x+2 x−2 x+2 x −4 a) Rót gän A. b) TÝnh gi¸ trÞ cña A khi x= - 4. c) T×m x∈Z ®Ó A∈Z. Bµi 3: (3 ®iÓm) Cho ∆ ABC vu«ng ë A (AB < AC ), ®êng cao AH. Gäi D lµ ®iÓm ®èi xøng cña A qua H. §êng th¼ng kÎ qua D song song víi AB c¾t BC vµ AC lÇn l - ît ë M vµ N. Chøng minh a) tø gi¸c ABDM lµ h×nh thoi. b) AM ⊥ CD . c) Gäi I lµ trung ®iÓm cña MC; chøng minh IN ⊥ HN.
ĐỀ 6: I. PHẦN TRẮC NGHIỆM: (4 điểm) Chọn câu trả lời đúng nhất (mỗi câu đúng đạt 0,5 điểm). x 2 -1 Câu 1: Kết quả thu gọn của phân thức: là: x(x-1) 2 1 x+1 A. B. C. D. 1 x x x Câu 2: Hình bình hành có một góc vuông là hình chữ nhật. A. Đúng B. Sai Câu 3: Số đo mỗi góc của ngũ giác đều là: A. 1080 B. 1800 C. 900 D. 600 Câu 4: Kết quả của phép chia (x – 2x + 1) : (x – 1) là: 2 C. (x + 1)2 D. (x – 1)2 A. x + 1 B. x – 1 x2 - 4 Câu 5: Điều kiện xác định của phân thức: 2 là: x + 2x A. x ≠ 0 B. x ≠ -2 C. x ≠ 0 và x ≠ 2 D. x ≠ 0 và x ≠ -2 1 22 1 Câu 6: Giá trị của biểu thức 3x3y2z : ( − x y z) tại x = − , y = 1, z = 2006 là: 3 9 A. -1 B. 9 C.1 D. 2006 Câu 7: Hình vuông có đường chéo bằng 4cm thì cạnh của nó bằng: A. 4 B. 8 C. 8 D. 2 Câu 8: Tam giác ABC vuông tại A. Diện tích của nó được tính theo công thức: 1 1 1 A. AB.AC B. AB.BC C. AC.BC 2 2 2 II. PHẦN TỰ LUẬN: (6 điểm) x 3 +2x 2 +x Bài 1: (2 điểm). Cho biểu thức: A = . x 2 +x a. Với giá trị nào của x thì giá trị của A xác định? b. Rút gọn biểu thức A rồi tính giá trị của A tại x =2005. Bài 2: (2 điểm). Tìm x, biết: a. x(x – 2) + x – 2 = 0 b. 5x(x – 3) – x + 3 = 0 Bài 3: (2 điểm). Cho hình thoi ABCD, biết hai đường chéo AC = 8cm, BD = 5cm. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. a. Tứ giác EFGH là hình gì? Vì sao? b. Tính diện tích tứ giác EFGH. ĐỀ 7: Câu 1 (1,5 điểm). Thực hiện phép tính: a) (x + 2) (x2 – 2x + 4) – (x3 + 2)
( ) b) 3x − 6x : 3x + ( 3x − 1) : ( 3x − 1) 2 2 Câu 2 (1,5 điểm). Phân tích các đa thức sau thành nhân tử: a) 5x 2 y − 10xy 2 b) 3(x + 3) – x2 + 9 Câu 3 (2,5 điểm). Cho biểu thức: 2 1 −1 4x 2 + 1 1 2 +2 − với x ≠ ; x ≠ ÷: 2 A=   1 + 2x 4x − 1 1 − 2x  4x − 1 2 2 a) Rút gọn biểu thức A. b) Tìm x, để A = 2. Câu 4 (3,5 điểm). Cho tam giác MNP vuông tại M, đường cao MH. Gọi D,E lần l ượt là chân các đường vuông góc hạ từ H xuống MN và MP. a) Chứng minh tứ giác MDHE là hình chữ nhật. b) Gọi A là trung điểm của HP, chứng minh tam giác DEA vuông. c) Tam giác MNP cần có thêm điều kiện gì để DE=2EA. Câu 5 (1 điểm). x−y x 2 + y 2 25 . Tính giá trị của biểu thức A = = Cho x < y < 0 và x+y xy 12 ĐỀ 8: Bai 1 ( 2đ): Phân tích các đa thức sau thành nhân tử: ̀ a/ 12x3 – 24x2 +12x b/ 16x2 – y2 – 2y – 1 c/ (x – 3)(x + 3) + (x – 3)2 d/ a(x – y) – b(y – x) Bai 2 (2,5 đ): Thực hiện phép tính: ̀ 1 11 1 a/ ( + ) : ( - ) y yx x 2x x −1 1 1 + − b/ ( ). x + 1 x −1 1 − x2 4x c/ Tìm số a để đa thức x3 – 3x2 + 7x – a chia hết cho đa thức x - 2 ̀ Bai 3 ( 1,5đ): 1/ Tìm x biết:
a/ (x – 3)(x – 5) – x2 = 0 12 (x2 – 9) = 0 b/ 2009 2/ Cho biểu thức A = x2 + 2x + 2 +y2. Chứng minh biểu thức A luôn luôn dương với mọi x, y? Bài 4(4điểm): Cho tam giác ABC, đường cao AH, trung tuyến AM. Trên tia AH, AM l ần l ượt lấy các điểm D, E sao cho HA = HD; MA = ME. Gọi K là chân đường vuông góc hạ từ E xuống BC. Chứng minh: a/ Tứ giác AKEH là hình bình hành? b/ Tứ giác HKED là hình chữ nhật c/ Tứ giác DBCE là hình thang cân d/ Cho DE = 30cm; AE = 50cm. Tính HM; DM?. ĐỀ 9: I/ Trắc nghiệm ( 2,5 điểm): Học sinh làm bài bằng cách khoanh tròn vào con chữ cái đứng trước câu trả lời đúng nhất trong 4 câu trả lời được cho dưới mỗi câu dẫn . Câu 1 : Biểu thức nào sau đây là các phân thức đại số ? x −1 d/ Cả a,b,c đều đúng a/ 0 b/ c/ 1 x +1 Câu 2 : Giá trị của (-x2y3) : (-3xy2) tại x = -2 ; y = -3 là : a/ 2 b/ -2 c/ 6 d/ -6 4 Câu 3 : Phân thức đối của phân thức là : 5− x −4 5− x 4 4 a/ − b/ − c/ d/ x−5 5− x x−5 4 x+2 Câu 4 : Phân thức nghịch đảo của phân thức là : x−2 −x−2 x−2 −x+2 −4 a/ b/ c/ d/ x−2 x+2 x−2 x−2 Câu 5 : Câu khẳng định nào sau đây là đúng ? a/ (a – b)2 = a2 – b2 b/ (a – b)2 = a2 – 2ab – b2 d/ Tất cả các câu trên đều sai c/ (a – b)2 = (b – a)2 Câu 6 : Các hình nhận giao điểm của 2 đường chéo làm tâm đối xứng của nó là : a/ Hình thang cân và hình chữ nhật b/ Hình bình hành và hình thoi c/ Hình chữ nhật và hình vuông d/ Cả b và c đều đúng Câu 7 : Một hình thoi có cạnh dài 20cm và một đuờng chéo dài 24cm . Đ ộ dài đ ường chéo kia của hình thoi đó là : a/ 32 cm b/ 34 cm c/ 30 cm d/ 16cm Câu 8 : Cho ∆ ABC vuông tại A có AB = 6cm , AC = 8cm . G ọi AM là trung tuy ến c ủa tam giác . Độ dài của đoạn thẳng AM là : a/ 5 cm b/ 4cm c/ 3 cm d/ 2 cm Câu 9 : Số trục đối xứng của hình vuông là : A/ 1 b/ 2 c/ 3 d/4
Câu 10: Cho tam giác ABC vuông tại A có đường cao là AH . Kh ẳng đ ịnh nào sau đây là đúng khi nói về diện tích của tam giác ABC ? 1 1 a/ S = BC. AH b/ S = AB. AC 2 2 c/ Câu a và câu b đều đúng d/ câu a đúng , câu b sai II/ Tự luận : ( 7,5 điểm) Bài 1 : ( 1 điểm) Phân tích đa thức thành nhân tử a/ x3 – x b/ 3x3 + 12x2 + 12x Bài 2 : ( 1 điểm ) Cho biểu thức A = ( a – b)2 + 4ab a) Rút gọn biểu thức A b) Tính giá trị của A khi a + b = -2 . Bài 3 : ( 2điểm ) Thực hiện các phép tính sau x+3 x +1 1  1 4 + − 1 −2 ⋅ b/ (x2 – 4)  a/  x+2 2− x  2x − 2 x − 1 2 ∧ Bài 4: ( 3,5 điểm ) Cho hình bình hành ABCD có AD = 2AB ; A = 600 . Gọi E , F là trung điểm của BC và AD . a/ Chứng minh rằng tứ giác ABEF là hình thoi b/ Chứng minh rằng tứ giác BFDC là hình thang cân c/ Lấy điểm M đối xứng với điểm A qua điểm B . Ch ứng minh t ứ giác BMCD là hình chữ nhật ĐỀ 10: I/ Trắc nghiệm ( 2,5 điểm): Học sinh làm bài bằng cách khoanh tròn vào con chữ cái đứng trước câu trả lời đúng nhất trong 4 câu trả lời được cho dưới mỗi câu dẫn . Câu 1 : Kết quả phép chia đa thức 2 x3 − 8x Câu 6 : Rút gọn phân thức 2x y +4x y - 6x y cho đơn thức (-2x y) là : 3 22 23 2 ( x + 2)( x − 2) , ta được kết quả là : a/ x2 -2y + 3y2 b/ - x +2y - 3y2 a/ x+2 b/ x-2 c/ -x2 + 2y + 3y2 d/ - x -2y + 3y2 2x c/ 2x d/ x−2 ˆˆˆ Câu 2 : Kết quả thực hiện phép tính ˆ , N , P, Q của hình thang Câu 7 : Tính M - 2xy ( 3x - 5y ) là : ˆˆ cân MNPQ ( MN // PQ ) biết M : Q = 2 : 1 . Kết quả là : (a) 6x2y - 10xy2 (b) - 6x2y + 10xy2 a/ 600, 600, 1200 , 1200 (c) 6x2y +10xy2 (d) - 6x2y -10xy2 b/ 600 ,1200 , 1200 , 60 c/ 1200 , 1200 , 600,600 d/ 1200, 600,600, 1200 Câu 3: Câu 8 : Cho x 2 - 8x + a = ( x - b )2 .Phải thay a, b Tứ giác ABCD là hình gì? nếu số đo các bởi cặp số nào trong các cặp số sau để góc A,C,B lần lượt bằng 850,950, 850 được một đẳng thức đúng ? (a) tứ giác lồi (a) a= 16 và b = 4 (b) a= 16 và b = 2 (b) hình thang cân
(c) a= 4 và b = 2 (d) a= 4 và b = 4 (c) hình bình hành (d) hình thoi Câu 9 : Hình vuông có cạnh bằng 5cm thì Câu 4 : Mẫu thức chung có bậc nhỏ nhất của các độ dài đường chéo của nó là: 2x − 1 2y 5 a/ 50cm b/ 50 cm ;2 ;2 phân thức 2 là : x − 4 x − 4x + 4 x − 2x c/ 25cm d/ 5 cm (a) (x - 2)2 (x+2) (b) x(x - 2)2(x+2) 2 (d) x(x - 2)(x+2)2 (c) (x - 2)(x+2) 6 −x Câu 10 : Một tứ giác là hình vuông nếu bằng các phân Câu 5 : Phán thæïc nó là x −1 a) tứ giác có ba góc vuông thức nào trong các phân thức sau : b) hình bình hành có một góc vuông x −6 (a) c) hình thang có một góc vuông 1−x d) hình thoi có một góc vuông x −6 (b) − x −1 6 −x (c) − 1−x (d) cả ba phân thức ở các câu a,b,c Pháön II : Tæû luáûn ( 7,5 điểm ) Baìi 1( 1 điểm ) : Phân tích đa thức thành nhân tử : a) 2a - 2ab2 b) a 2 - 2a + 1 - b 2 Bài 2 ( 1,5điểm ) : Chứng minh rằng biểu thức sau không phụ thuộc vào biến x : ( x +2 )2 - 2 (x +3)(x - 3) + (x- 1)( x-3) Bài 3 ( 1,5 điểm ) : Thực hiện phép tính 1 3 3 + −2 x −1 1 − x x + x +1 3 Bài 4 ( 3,5 điểm ) : Cho tam giác nhọn ABC. Gọi D, E, F lần lượt là trung điểm của các cạnh AC, AB, BC . a) Tứ giác BCDE là hình gì ? Vì sao ? b) Tứ giác BEDF là hình gì ? Vì sao ? c) Gọi H là trực tâm của tam giác ABC . M, N, P lần lượt là trung điểm của HB, HC, HA . Chứng minh rằng tứ giác DEMN là hình chữ nhật . d) Gọi O là giao điểm của MD và EN . Chứng minh r ằng ba đi ểm O, P, F th ẳng hàng ĐỀ 11: I/ Trắc nghiệm ( 2,5 điểm): Học sinh làm bài bằng cách khoanh tròn vào con chữ cái đứng trước câu trả lời đúng nhất trong 4 câu trả lời được cho dưới mỗi câu dẫn . Câu 1 : Kết quả của phép tính (2x2 – 32) : (x – 4) là : a/ 2(x – 4) b/ 2(x + 4) c/ x + 4 d/ x - 4
Câu 2 : Với x = 105 thì giá trị của biểu thức x2 – 10x + 25 bằng : a/ 1000 b/ 10000 c/ 1025 d/ 10025 x+2 x +1 Câu 3 : Mẫu thức chung của 2 phân thức bằng : 2 và x−x 2 − 4x + 2x 2 a/ 2(1 – x)2 b/ x(1 – x)2 d/ 2x(1 – x)2 c/ 2x(1 – x) 3x − 1 Câu 4 : Điều kiện xác định của phân thức là : 9x 2 − 1 1 1 1 1 a/ x ≠ b/ x ≠ − c/ x ≠ và x ≠ − d/ x ≠ 9 3 3 3 3 x −1 x −1 : Câu 5 : Kết quả của phép tính là : x 2 x 2 1 a/ 2x b/ c/ d/ 2 x 2x Câu 6 : Cho ABCD là hình thang ( AB // CD),biết số đo c ủa góc BCD b ằng 60 0 . Số đo của góc ABC là : a/ 600 b/ 1300 c/1500 d/ 1200 Câu 7 : Độ dài 2 đường chéo của một hình thoi bằng 4 cm và 6 cm . Độ dài cạnh hình thoi là : a/ 13 cm b/ 13 cm c/ 52 cm d/ 52 cm Câu 8 : Câu khẳng định nào sau đây sai ? a/ Hình thang có hai cạnh bên bằng nhau là hình thang cân b/ Tứ giác có 2 cạnh đối song song là hình thang c/ Hình thang cân có 1 góc vuông là hình chữ nhật d/ Hình chữ nhật có 2 đường chéo vuông góc là hình vuông Câu 9 : Cho ∆ ABC vuông tại A có AB = 6cm , AC = 8cm . Gọi AM là trung tuyến của ∆ ABC . Độ dài của đoạn thẳng AM là : a/ 5 cm b/ 4cm c/ 3 cm d/ 2 cm Câu 10 : Hãy điền chữ Đ(hoặc S) vào ô tương ứng nếu các câu sau là đúng (hoặc sai) Cho hình chữ nhật ABCD , M thuộc đoạn AB . Khi đó ta có : a/Diện tích của tam giác MDC không đổi khi điểm M thay đổi vị trí trên đoạn thẳng AB b/ Diện tích của tam giác MDA sẽ thay đổi khi điểm M thay đổi vị trí trên đoạn thẳng AB II/ Tự luận : ( 7,5 điểm) Bài 1: ( 2 điểm) Phân tích đa thức thành nhân tử b/ 100 – x2 + 2xy – y2 a/ x(y – 1) – 2(1 – y) Bài 2: ( 1,5 điểm ) Cho biểu thức :
1  x2 − x +1  A = x− : 2  1− x  x − 2x + 1 a/ Rút gọn biểu thức A b/ Tính giá trị của A khi x = -1 Bài 3: (0,5 điểm ) Cho x + y + z = 0 ; x , y , z khác 0 . Tính giá trị của biểu thức :  x  y  z  1 +   1 +  1 +    y  z  x  Bài 4: (3,5 điểm ) Cho hình thang ABCD cân ( AB //CD). Gọi M, N, I , K l ần l ượt là trung điểm của các cạnh AD,BC, AB,CD. a/ Chứng minh tam giác AKB cân b/ Tứ giác MINK là hình gì ? Tại sao ? c/ Chứng minh IK vuông góc với MN ĐỀ 12: Bài 1 : (2điểm) Phân tích đa thức sau thành nhân tử : a) 5x2 - 5x b) 3x2 - 6x + 3 Bài 2( 1 điểm ) Rút gọn biểu thức sau (x +2y)2 - ( 2x - y)(x + 2y) 1− x  1 1 1 − +2   Bài 3 : ( 2 điểm ) Cho biểu thức A =  x − 2 x − 2  x + 2 x + 2x a) Rút gọn biểu thức A b) Tính giá trị của A tại x = -1 Bài 4 : (3, 5 điểm ) Cho hình thang ABCD ( AB // CD ) . Gọi E, F, G, H lần lượt là trung điểm của AB, AC , CD , DB a) Chứng minh tứ giác EFGH là hình bình hành . b) Nếu ABCD là hình thang cân thì tứ giác EFGH là hình gì ? Vì sao ? ˆ c) Nếu ABCD là hình thang cân và có D = 450 thì tứ giác EFGH là hình gì ? Vì sao ? x2 − 3 Bai 5:(1,5đ) Tim giá trị nguyên cua x để biêu thức M = ̀ ̀ ̉ ̉ có giá trị nguyên x−2 ĐỀ 13: Bài 1: (1,5đ) Phân tích các đa thức sau thành nhân tử: b) x 3 y − xy 3 − 2 xy 2 − xy a) 2ab 4 − 8ab3 + 8ab 2 Bài 2: (1,5 đ) Tìm x biết: a) 2 x ( x − 5 ) − x ( 3 + 2 x ) = 26 b) 2 ( x + 5 ) − x − 5 x = 0 2
1  x2 + 4x + 4 1 Bài 3: (2,5đ) Cho biểu thức A =  − ÷×  x−2 x+2 4 a) Tìm điều kiện của x để A có nghĩa. b) Rút gọn A c) Tìm giá trị của x để A = 0 Bài 4: (2,5đ) Cho hình chữ nhật ABCD (AB > BC). Gọi E là điểm đối xứng của B qua A, F là điểm đối xứng của B qua C. a) Tứ giác ADFC là hình gì? Vì sao? b) Chứng minh E, D, F thẳng hàng. c) Chứng minh ∆ BDE và ∆ BDF có diện tích bằng nhau. y   x2 − y2  x +2 ÷:  ÷ Bai 5: (2đ) Thưc hiên phep tinh:  2 ̀ ̣ ̣ ́́ y − xy x − xy   x 2 y + xy 2  