Bùi Gia Phong − Giáo viên trng THPT Trng Vnh Ký Bn tre.
 I − TOÁN ÔN THI TT NGHIP THPT
I/ PHN CHUNG CHO TT C CÁC THÍ SINH (7,0 im).
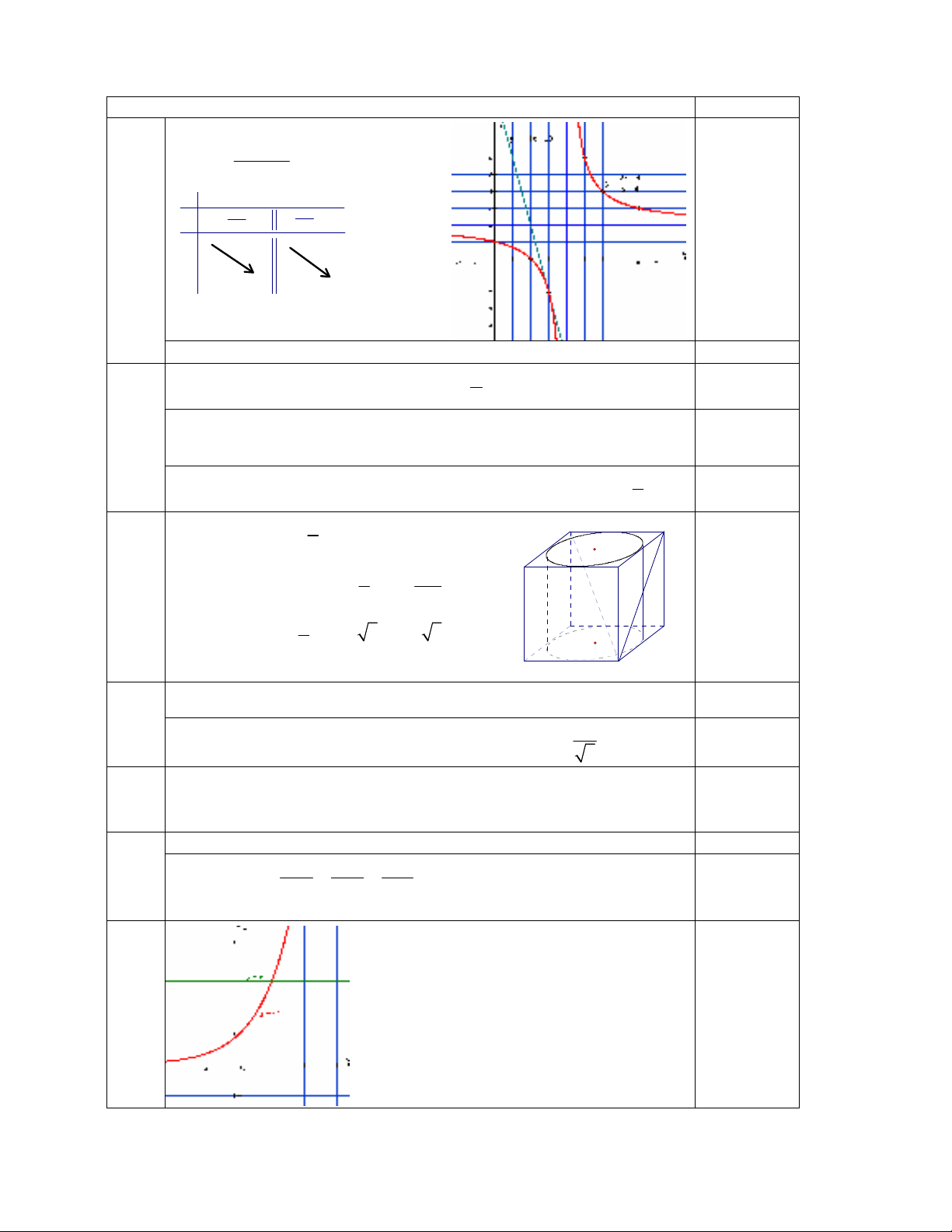
Câu I (3,0 im). Cho hàm s
2x 4
y
x 4
−
=
−
có  th (H).
a) Kho sát s bin thiên và v  th (H).
b) Vit phng trình tip tuyn vi (H) ti im tung  bng −2.
Câu II (3,0 im).
1) Cho y = xlnx. Chng minh rng: x2y’’ − xy’ + y = 0.
2) Gii bt phng trình: log4(x + 7) > log2(x + 1).
3) Tính:
1
x
0
x
I dx
e
=
Câu III (1,0 im). Cho hình lp phng ABCD.A’B’C’D’ có cnh bng a.
a) Tính th tích ca khi tr có hai áy là hai hình tròn ni tip hai mt i din ca hình lp
phng ABCD.A’B’C’D’.
b) Tính din tích xung quanh ca hình nón to thành khi cho tam giác ABC’ quay quanh
ng thng BC’.
II/ PHN RIÊNG (3,0 im).
1) Theo chng trình Chun:
Câu IV.A) (2,0 im).
Trong không gian Oxyz cho A(6; −2; 3), B(0; 1; 6),
OC 2i k
= −
,
OD 4i j
= +
.
a) Chng minh rng ABCD là hình t din. Tính th tích t din ABCD.
b) Vit phng trình mt phng (ABC) và tính chi u cao h t! D ca t din ABCD.
Câu V.A) (1,0 im). Cho hai s phc z1 = 5 − 7i và z2 = 4 − 3i.
Tìm ph"n thc, ph"n o ca s phc z = z1.z2. Tính (z1)3.
2) Theo chng trình Nâng cao:
Câu IV.B) (2,0 im). Trong không gian Oxyz cho hai im M(1; 1; 1), N(2; −1; −2) và mt c"u
(S) có phng trình: x2 + y2 + z2 − 2x + 4y − 6z − 2 = 0.
a) Tìm tâm, bán kính và din tích ca mt c"u (S).
b) Vit phng trình chính t#c ca ng thng MN và xét v trí tng i ca ng thng
MN vi mt c"u (S).
Câu V.B) (1,0 im). Tính th tích khi tròn xoay to thành khi cho hình phng gii hn b$i các
ng y = ex, y = e, x = 0 quay quanh trc tung.
Bùi Gia Phong − Giáo viên trng THPT Trng Vnh Ký Bn tre.
C'
D'
B'
A'
DC
B
A
Tóm t#t cách gii I. Thang im
a) TX: D = R\{4}.
2
4
y'
(x 4)
−
=−.
x
y
y'
-∞+∞
4
2
2
-∞
+∞
TC: x = 4 ; TCN: y = 2.
2,0
I
b) y0 = −2 x0 = 3 PTTT y = −4x + 10.1,0
1) y’ = lnx + 1
1
y''
x
=
pcm. 1,0
2)
2
x 1 0
x 7 (x 1)
+ >
+ > +
−1 < x < 2 1,0
II/
3) u = x du = dx ; dv = e−x dx . Ch%n v = −e−x
2
I 1
e
= −
1,0
III/ a)
a
R
2
=
; h = a.
2
3
2
a a
V R h a
2 4
π
= π = π =
b) 2
xq
1
S .2 .a.a 3 a 3
2
= π = π
1,0
a)
AB( 6;3;3), AC( 4;2 4)
− − −
;
AB, AC ( 18; 36;0)
= − −
; V = 12. 1,0
IV.A)
b) (ABC): x + 2y − 2 = 0
4
d(D, (ABC))
5
= 1,0
V.A) z = 20 −15i − 28i + 21 i2
z = −1 − 43i ph"n thc −1; ph"n o −43
(5 − 7i)3 = − 610 − 182i.
1,0
a) I(1; −2; 3); R = 4; S = 4πR2 = 64π. 1,0
IV.B)
b)
x 1 y 1 z 1
1 2 3
− − −
= =
− −
d(I, MN) < R pcm.
(Hoc im M nm trong mt c"u ng thng MN c#t mt c"u)
1,0
V.B)
x
y e
y e
x 0
=
=
=
x ln y
x 0
y e
y 1
=
=
=
=
e
2
1
V (ln y) dy
= π
u = (lny)2 ; dv = dy
(Tích phân t!ng ph"n hai l"n )
V = π(e − 2) (vtt).
1,0
Bùi Gia Phong − Giáo viên trng THPT Trng Vnh Ký Bn tre.
 II − TOÁN ÔN THI TT NGHIP THPT
I/ PHN CHUNG CHO TT C CÁC THÍ SINH (7,0 im).
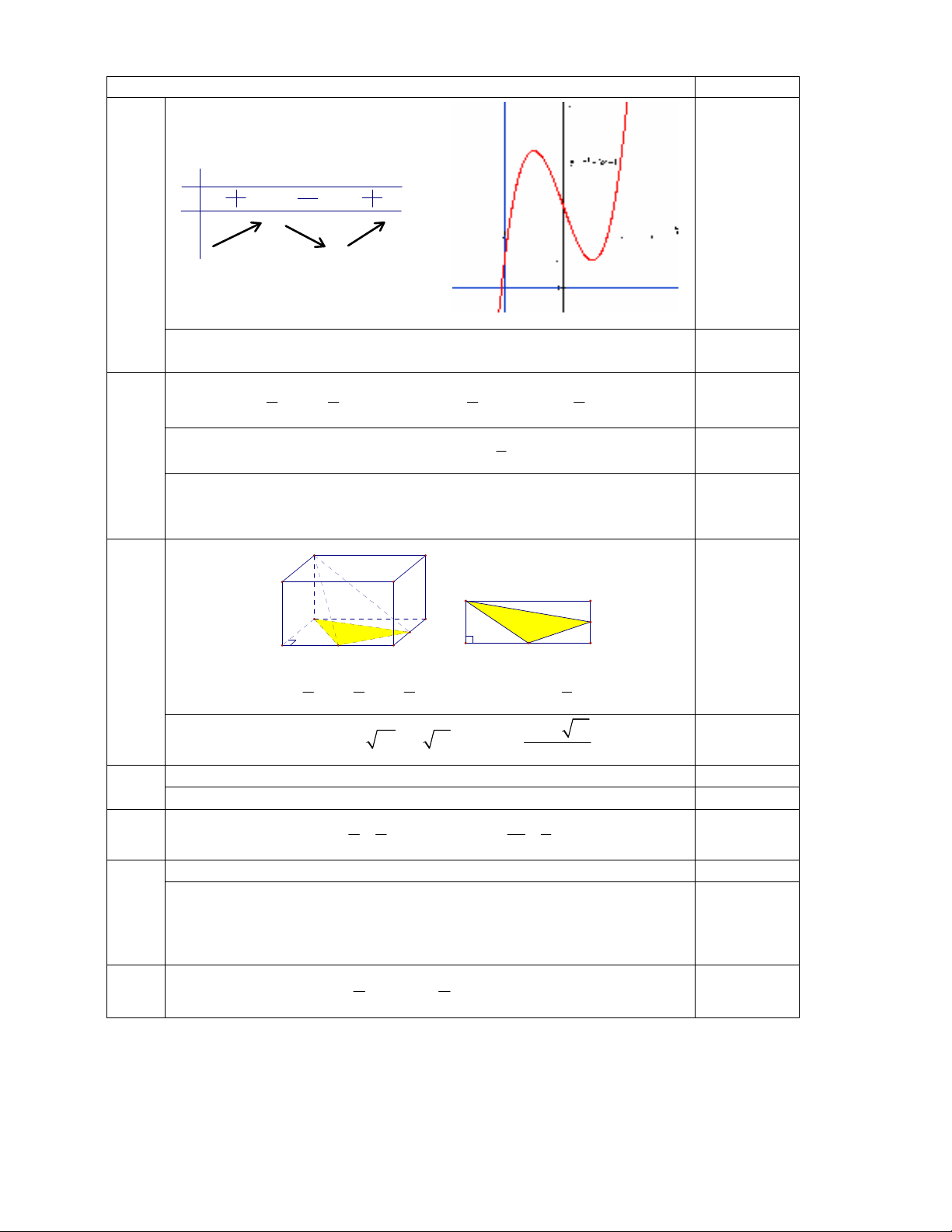
Câu I (3,0 im). Cho hàm s y = x3 − 3x + 1 có  th (C).
a) Kho sát s bin thiên và v  th (C).
b) Tìm m  phng trình: x3 − 3x + 6 − 2−m = 0 có ba nghim phân bit.
Câu II (3,0 im).
1) Gii phng trình: 4.9x + 12x − 3.16x = 0.
2) Tính tích phân
2
e
3
e
dx
I dx
x.ln x
=.
3) Tìm giá tr ln nht và giá tr nh& nht ca hàm s f(x) = x2e−x trên on [−1; 3].
Câu III (1,0 im). Cho hình hp ch' nht ABCD.A’B’C’D’ có AB = 6, AD = 8, AA’ = 10. G%i M,
N l"n l(t là trung im ca A’B’ và B’C’.
a) Tính th tích khi t din D’DMN.
b) Tính th tích ca khi tròn xoay to thành khi cho ∆D’DN quay quanh D’N.
II/ PHN RIÊNG (3,0 im).
1) Theo chng trình Chun:
Câu IV.A) (2,0 im).
Trong không gian Oxyz cho mt phng (P) có phng trình x + y + z − 10 = 0 và ng thng
∆ có phng trình
x 1 4t
y 3 5t
z 2 t
= − +
= − −
= +
.
a) Chng minh rng ng thng ∆ song song vi mt phng (P).
b) Vit phng trình mt phng (Q) cha ∆ và vuông góc vi (P).
Câu V.A) (1,0 im). Tìm ph"n thc và ph"n o ca s phc
3
2 3i
z (1 i)
1 2i
+
= + −
−
.
2) Theo chng trình Nâng cao:
Câu IV.B) (2,0 im).
Trong không gian Oxyz cho mt phng (P) có phng trình x + y + z − 10 = 0 và ng
thng ∆ có phng trình
x y 1 z 3
2 1 1
− −
= =
−
.
a) Chng minh rng ∆ c#t mt phng (P). Tìm giao im ca ∆ và (P).
b) Vit phng trình ng thng ∆’ là hình chiu vuông góc ca ∆ trên (P).
Câu V.B) (1,0 im). Vit s phc
z 2 2i 3
= − di dng l(ng giác và tính z6.
Bùi Gia Phong − Giáo viên trng THPT Trng Vnh Ký Bn tre.
Tóm t#t cách gii II. Thang im
a) TX: D = R.
y’ = 3x2 − 3
y’ = 0 x = ±1
-1
3
1
+∞
x
y
y'
-∞+∞
-∞
00
-1
y’ = 6x
y’’ = 0 x = 0
im un U(0; 1).
2,0
I
b) x3 − 3x + 6 − 2−m = 0 x3 − 3x + 1 = 2−m −5.
−1 < 2−m − 5 < 3 −3 < m < −21,0
1)
2 2x
4 4
4 3 0
3 3
+ − =
. t
x
4
y 0
3
= >
4
y
3
=
x = 1. 1,0
2) t t = lnx
3
I
8
=
1,0
II/
3) TX: D = R. f’(x) = (2x − x2)e−x . f’(x) = 0 x = 0 hoc x = 2.
f(−1) = e; f(0) = 0; f(2) = 4e−2; f(3) = 9e−3.
maxf(x) = f(−1) = e ; minf(x) = f(0) = 0.
1,0
a)
// //
\
\N
MB'A'
D'
D
C'
C
B
A
_
_
N
B'
M
////
D'
A'
C'
D'MN
1 1 1
S 6.8 6.4 3.4 8.3 18
2 2 2
= − − − =
D'DMN
1
V 18.10 60
3
= =
0,5
III/
b) r = 10;
h 52 2 13
= = nón
200 13
V
3
π
= 0,5
a) H PT vô nghim ∆ // (P). 1,0
IV.A)
b) (Q): 2x + y − 3z + 8 = 0. 1,0
V.A)
4 7 14 3
z i ( 2 2i) i
5 5 5 5
= − + + − − = − −
1,0
a) Gii h phng trình (6; −2; 6). 1,0
IV.B)
b) ∆’ = (P) ∩ (Q) vi (Q): 2x + y − 3z + 8 = 0
x 18 4t
': y 28 5t
z t
= − +
∆ = −
=
1,0
V.B) z 4 cos isin
3 3
π π
= − + −
z6 = 46 = 4096. 1,0
Bùi Gia Phong − Giáo viên trng THPT Trng Vnh Ký Bn tre.
 III − TOÁN ÔN THI TT NGHIP THPT
I/ PHN CHUNG CHO TT C CÁC THÍ SINH (7,0 im).
Câu I (3,0 im). Cho hàm s y = − x4 + 6x2 − 5 có  th (C).
a) Kho sát s bin thiên và v  th (C).
b) Vit phng trình tip tuyn ca (C) ti im có hoành  th&a f’’(x) = 0.
Câu II (3,0 im).
1) Gii bt phng trình: 1 2
2
x
log log (x 1)
2 x
< − −
−
.
2) Tính tích phân
5
1
2
I x 2x 1 dx
= −
.
3) Tìm giá tr nh& nht ca hàm s f(x) = xlnx.
Câu III (1,0 im). Cho hình t din u ABCD có cnh bng a.
a) Tính th tích khi t din ABCD.
b) Tính din tích mt c"u ngoi tip t din ABCD.
II/ PHN RIÊNG (3,0 im).
1) Theo chng trình Chun:
Câu IV.A) (2,0 im). Trong không gian Oxyz cho ng thng ∆ có phng trình
x 3 y 2 z 6
2 3 4
+ + −
= = và ng thng ∆’ có phng trình
x t
y 19 4t
z 15 t
=
= +
= −
.
a) Chng minh rng ∆ c#t ∆’. Tìm giao im ca ∆ và ∆’.
b) Vit phng trình mt phng xác nh b$i ∆ và ∆’.
Câu V.A) (1,0 im). Tính din tích hình phng gii hn b$i  th hàm s y = sinx, trc hoành
và hai ng thng x = π, x = − π.
2) Theo chng trình Nâng cao:
Câu IV.B) (2,0 im). Trong không gian Oxyz cho ng thng ∆ có phng trình
x 5 6t
y 1 2t
z 5 4t
= −
= −
= +
và
ng thng ∆’ có phng trình
x 6 z 11
y
3 2
+ −
= =
−
.
a) Chng minh rng ∆ và ∆’ ng phng.
b) Vit phng trình mt phng xác nh b$i ∆ và ∆’.
Câu V.B) (1,0 im). Gii phng trình: z2 − 2iz − 8 + 24i = 0 trên tp s phc.