CH NG 2ƯƠ
V T D N - Đi N MÔIẬ Ẫ Ệ
TR NG Đ I H C CÔNG NGHI P TP. H CHÍ MINHƯỜ Ạ Ọ Ệ Ồ
KHOA KHOA H C C B NỌ Ơ Ả
GIAÙO TRÌNH VAÄT LYÙ ÑAÏI CÖÔNG
PHAÀN 2: ÑIEÄN - TÖØ HOÏC
GV: PGS.TS. NGUYEÃN KHAÙNH
DUÕNG
BÀI 1
V T D N CÂN B NG Ậ Ẫ Ằ
TĨNH Đi NỆ
§1. V t d nậ ẫ
1.1. V t d n:ậ ẫ
- V t d nậ ẫ là nh ng v t có các ph n t ữ ậ ầ ử
t i đi n chuy n đ ng t do trong toàn ả ệ ể ộ ự
v t (kim lo i d n đi n t t).ậ ạ ẫ ệ ố
- V t cách đi nậ ệ (đi n môi) là nh ng v t ệ ữ ậ
không có các ph n t t i đi n t do, ầ ử ả ệ ự
đi n tr r t l n (các ch t vô c ).ệ ở ấ ớ ấ ơ
- Bán d nẫ là các ch t trung gian gi a ấ ữ
d n đi n và cách đi nẫ ệ ệ
Gi i thích tính ch t d n đi n c a v t d n ả ấ ẫ ệ ủ ậ ẫ
theo thuy t ếc u t o nguyên tấ ạ ử và thuy t ế
vùng năng l ngượ .
1.2. V t d n cân b ng tĩnh đi nậ ẫ ằ ệ
a. Đ nh nghĩaị - Đi u ki n cân b ng tĩnh ề ệ ằ
đi nệ
-V t d n có các ậ ẫ ph n t t i đi nầ ử ả ệ tr ng ở ạ
thái n đ nh (t do), không chuy n đ ng.ổ ị ự ể ộ
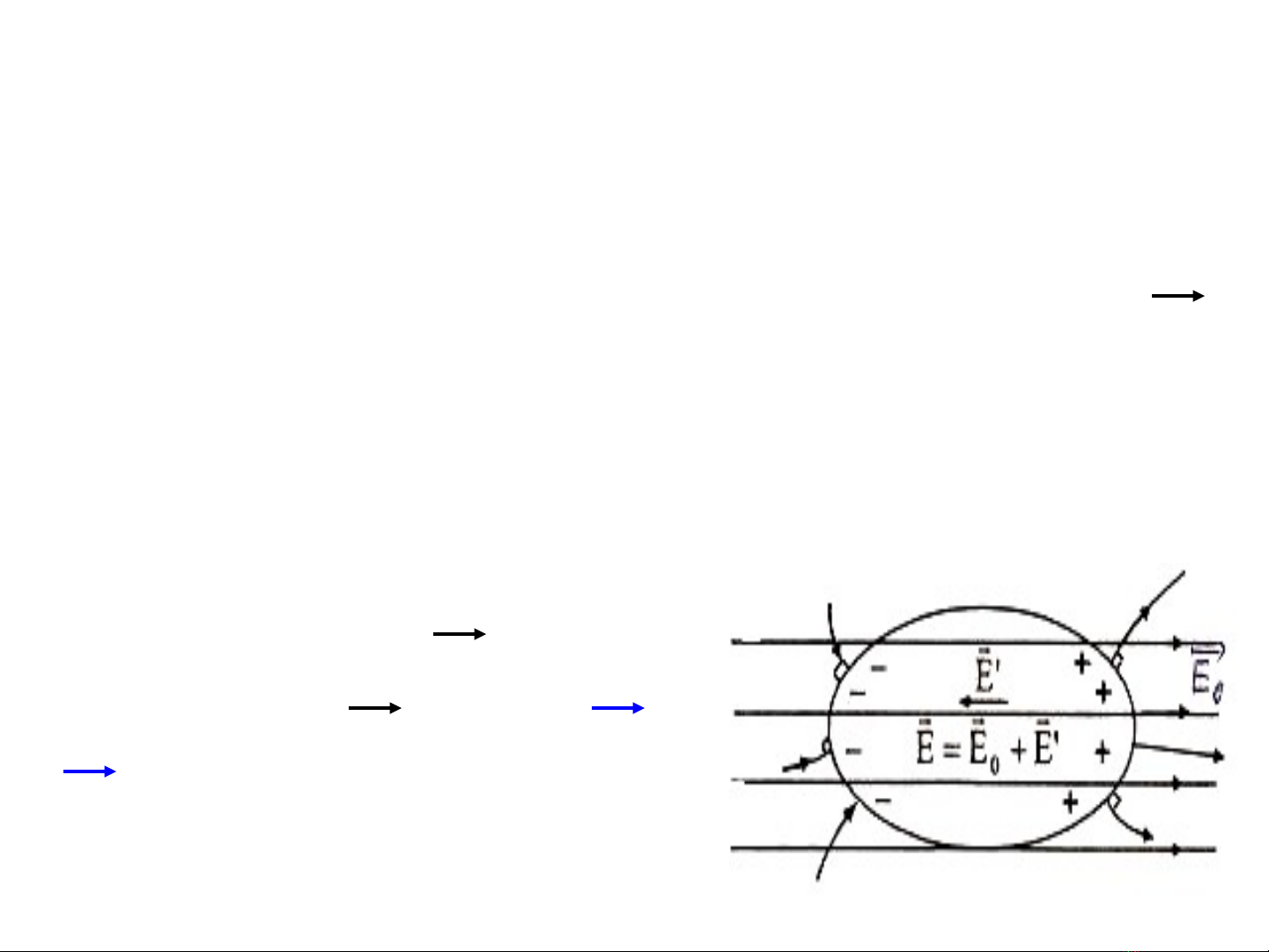
-Khi đ t v t d n vào đi n tr ng ngoài Eặ ậ ẫ ệ ườ o,
các đi n tích d ngệ ươ chuy n đ ng v m t ể ộ ề ộ
phía theo chi u đi n tr ng, các ề ệ ườ đi n tích ệ
âm chuy n đ ng theo chi u ng c l i. ể ộ ề ượ ạ
Trong v t d n xu t ậ ẫ ấ
hi n đi n tr ng E’ ệ ệ ườ
ng c chi u v i Eượ ề ớ o. Khi
E’ = Eo, tr ng thái cân ạ
b ng đ c thi t l p.ằ ượ ế ậ
- Đ có s cân b ng tĩnh đi n c n đi u ể ự ằ ệ ầ ề
ki n:ệ
+ Véct c ng đ đi n tr ng bên ơ ườ ộ ệ ườ
trong v t d n b ng 0: ậ ẫ ằ Etr = Eo+E’ = 0.
+ b m t c a v t d n véc t c ng Ở ề ặ ủ ậ ẫ ơ ườ
đ đi n tr ng ộ ệ ườ E vuông góc v i m t ớ ặ
v t d n.ậ ẫ Thành ph n ti p tuy n ầ ế ế Et c a ủ
véct ơE ph i b ng 0 t i m i đi m trên ả ằ ạ ọ ể
m t v t d n:ặ ậ ẫ Et = 0 và E = En