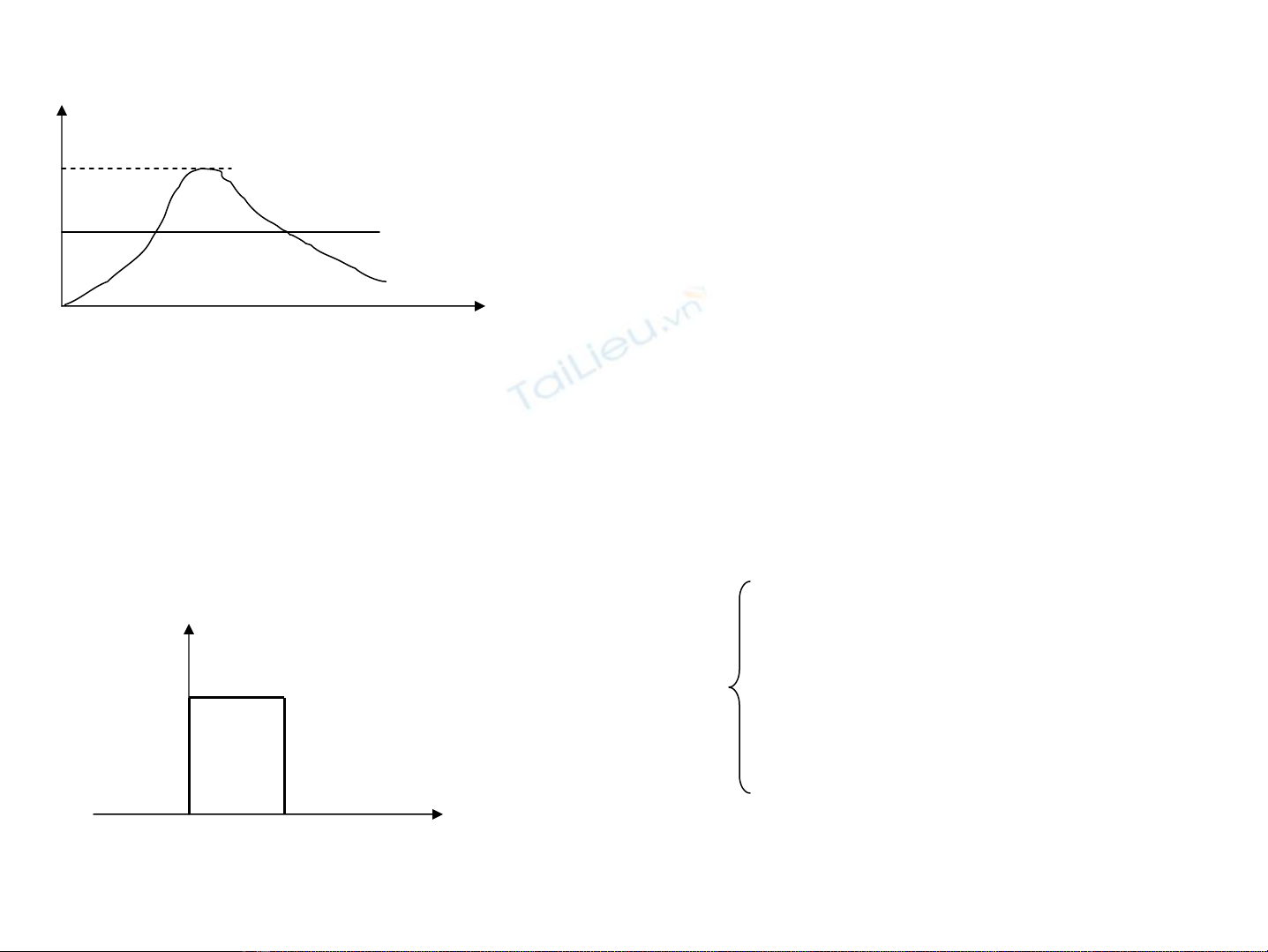
5.2. HiÖu øng ®−êng hÇm
U
Umax W
x
§èi víi c¬ cæ ®iÓn nÕu n¨ng
l−îng h¹t W<U th× h¹t
kh«ng v−ît qua ®−îc hμng
rμothÕ
§èi víi c¬ häc LT vi h¹t cã kh¶ n¨ng xuyªn qua
hμng rμo thÕ cao h¬n n¨ng l−îng cña nã: HiÖu
øng xuyªn hÇm
U
x
a0
U0
III III
ψ1(x) ψ2(x) ψ3(x) U= 0 x≤0 miÒn I
U00<x<a miÒn II
0 x≥a miÒn III
Ph−¬ng tr×nh Schrodinger cho ba vïng
2
1
2
1
21
2mW2
0k
dx
d
h
==ψ+
ψ2
1
kvíi
)WU(
m2
0k
dx
d
0
2
2
2
2
22
2−==ψ+
ψ
h
2
2
kvíi
2
3
2
1
23
2mW2
0k
dx
d
h
==ψ+
ψ2
1
kvíi
miÒn I
miÒn II
miÒn III
NghiÖm cña c¸c ph−¬ng tr×nh: xik
1
xik
11 11 eBeA)x( −
+=ψ
xk
2
xk
22 22 eBeA)x( −
+=ψ )ax(ik
3
)ax(ik
33 11 eBeA)x( −−− +=ψ
HÖ sè truyÒn qua
/xuyªn hÇm 2
1
2
3
*
11
*
33
|A|
|A|
D=
ψψ
ψψ
=
Theo tÝnh chÊt liªn tôc cña hμm sãng vμ®¹o hμm
bËc nhÊt cña hμm sãng.
T¹i c¸c bê:
ψ1(0)= ψ2(0)
ψ’1(0)= ψ’2(0)
ψ2(a)= ψ3(a)
ψ’2(a)= ψ’3(a)
C¸c hÖ thøc:
A1+B1= A2+B2
ik1(A1-B1)= -k2(A2+B2)
A2e-k2a+B2ek2a= A3
-k2(A2e-k2a+B2ek2a)=ik1A3
B3=0, kh«ng cã sãng ph¶n x¹ tõ v« cïng
Tõ 2 ph−¬ng tr×nh cuèi x¸c ®Þnh A2, B2qua A3
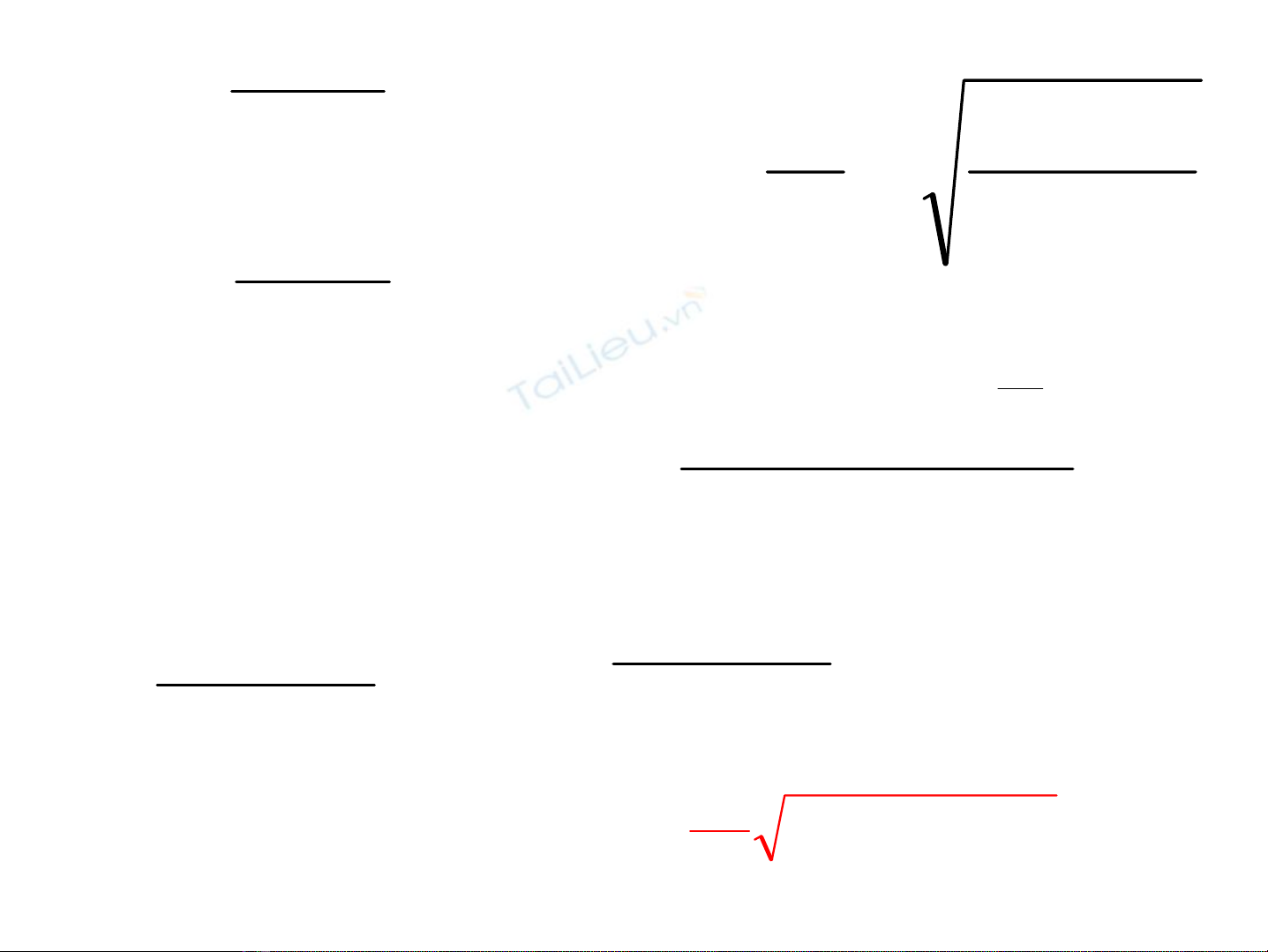
ak
32 2
eA
2
in1
A−
=
ak
32 2
eA
2
in1
B−
+
=WU
W
k
k
n
02
1
−
==
Coi W<<U0hoÆc
bÒ réng cña hμng
rμolínk2a>>1
ak
31 2
eA
4
)
n
i
1)(in1(
A+−
=
ak2
2
2
2
e
)n1(
n16
D−
+
=1~
)n1(
n16
2
2
+(U0~10W)
)WU(m2
a2
ak2 0
2eeD −−
−== h
MÆc dï W<U0vÉn cã h¹t xuyªn qua hμng rμoth
Õ
Víi ®iÖn tö m=9,1.10-31kg, U0-W=1,28.10-31J
a(m) 10-10 1,5.10-10 2.10-10 5.10-10
D 0,1 0,03 0,008 5.10-7
D ®¸ng kÓ khi a nhá: HiÖu øng xuyªn hÇm chØ
x¶y ra ë kÝch th−íc vi m«
=> TÝnh sãng cña vi h¹t
Ph¸t x¹ ®iÖn tö l¹nh
Ph©n r· h¹t α