
1
CHƢƠNG 4:
XỬ LÝ NÂNG CAO CHẤT LƢỢNG
ẢNH
(image enhancement)
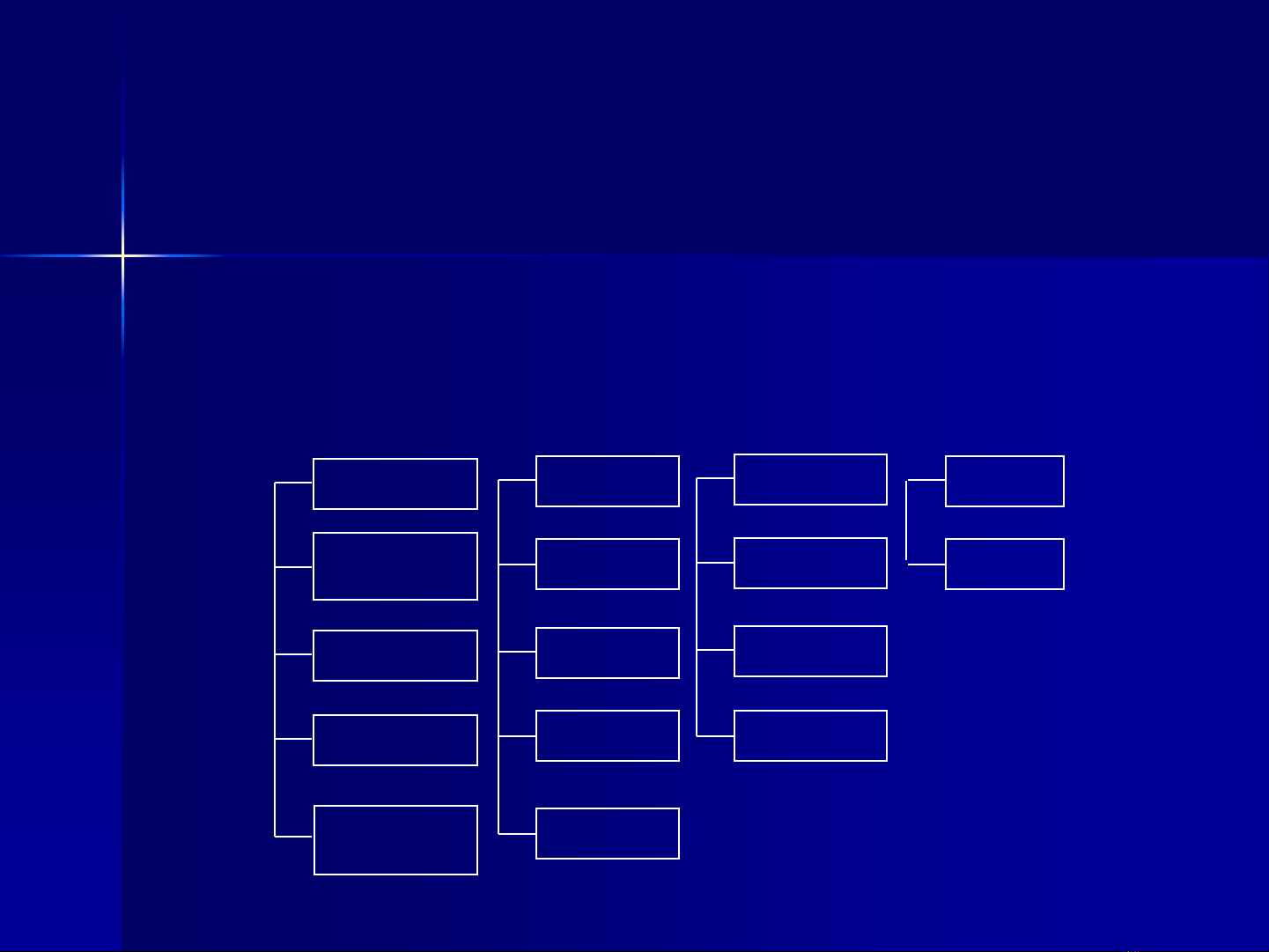
4.1. CÁC KỸ THUẬT TĂNG CƯỜNG ẢNH
(Image Enhancement)
Nhiệm vụ của tăng cường ảnh không phải là làm tăng lượng thông
tin vốn có trong ảnh mà làm nổi bật các đặc trưng đã chọn làm sao
để có thể phát hiện tốt hơn, tạo thành quá trình tiền xử lý cho phân
tích ảnh.
To¸n tö ®iÓm
T¨ng ®é t-¬ng
ph¶n
Xo¸ nhiÔu
Chia cöa sæ
M« h×nh ho¸
l-îc ®å
To¸n tö KG
Läc trung
vÞ
Tr¬n nhiÔu
Läc d¶i thÊp
Tr¬n ¶nh
BiÕn ®æi
Läc gèc
Läc tuyÕn
tÝnh
Läc s¾c thÓ
Gi¶ mµu
Sai mµu
H×nh 4.1. C¸c kü thuËt c¶i thiÖn ¶nh

Nâng cao chất lƣợng ảnh
là bước cần thiết trong xử lý
ảnh nhằm hoàn thiện một số đặc tính của ảnh.
Nâng cao chất lượng ảnh gồm hai công đoạn khác nhau:
tăng cường ảnh và khôi phục ảnh. Tăng cường ảnh nhằm
hoàn thiện các đặc tính của ảnh như :
-Lọc nhiễu, hay làm trơn ảnh,
-Tăng độ tương phản, điều chỉnh mức xám của ảnh,
-Làm nổi biên ảnh.
Các thuật toán triển khai việc nâng cao chất lượng ảnh hầu
hết dựa trên các kỹ thuật trong miền điểm, không gian và
tần số. Toán tử điểm là phép biến đổi đối với từng điểm
ảnh đang xét, không liên quan đến các điểm lân cận khác,
trong khi đó, toán tử không gian sử dụng các điểm lân cận
để quy chiếu tới điểm ảnh đang xét.

4
XỬ LÝ ĐIỂM
Toán tử Thoạt động tại mỗi vùng lân cận của vị trí điểm
ảnh (x, y) trong ảnh f để cho ảnh đầu ra g tương ứng.
Ttác động lên vùng lân cận có kích thước 11 (tác động
lên điểm đơn) g chỉ phụ thuộc vào giá trị của f tại điểm
(x, y), và T trở thành hàm biến đổi cấp xám có dạng:
s = T(r)
r = f(x, y)
s = g(x, y)
Kỹ thuật này được gọi là kỹ thuật xử lý điểm
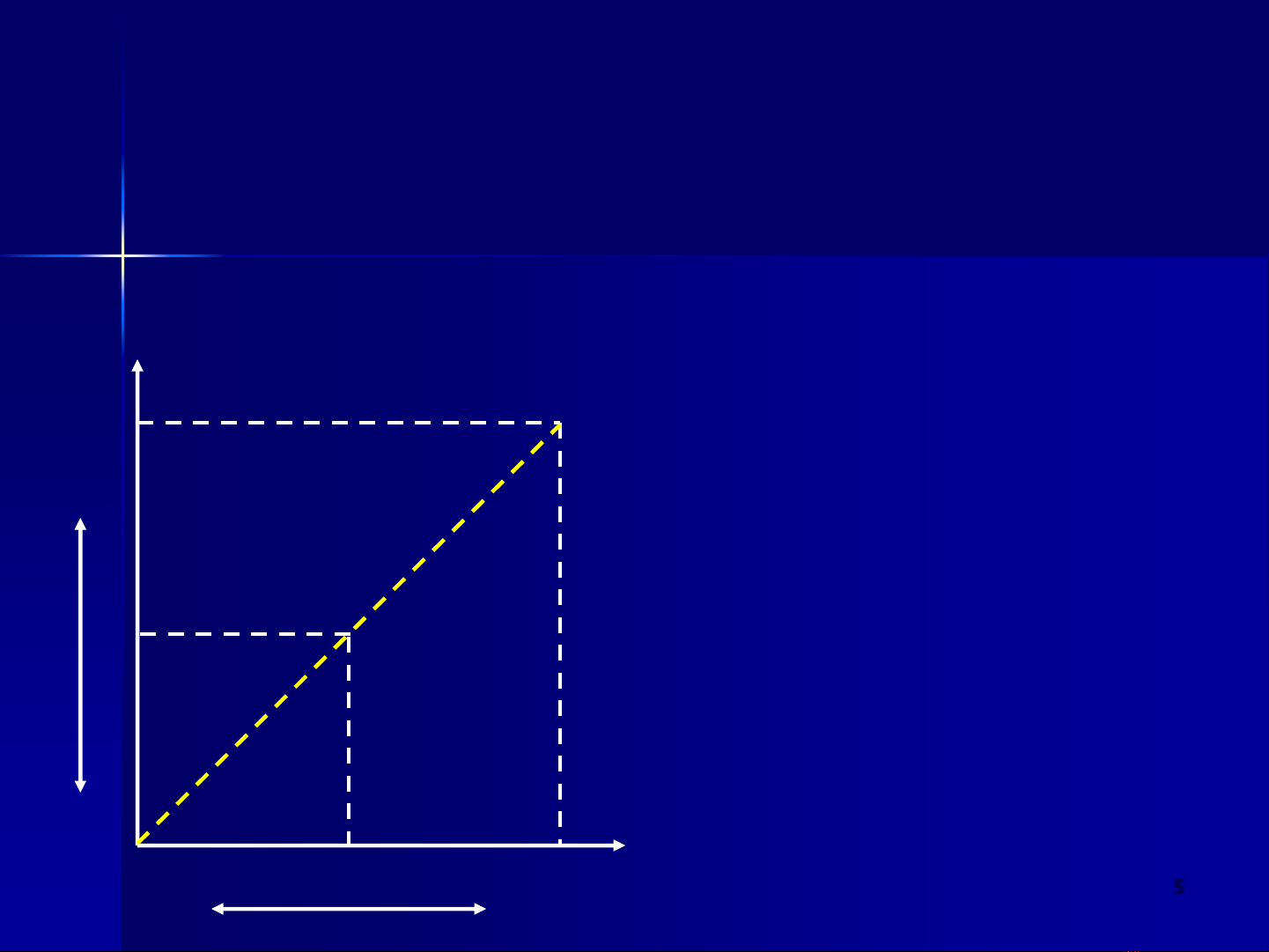
5
BIẾN ĐỔI ĐỒNG NHẤT
Ví dụ: Hàm biến đổi đồng nhất các điểm ảnh
r
s=T(r)
m
T(r)
Tối Sáng
Tối Sáng
Hàm biến đổi đồng nhất T(r).
Ảnh kết quả có độ tương phản
giống với ảnh gốc.
m


























