2 đề thi HK2 Toán 10 - (Kèm Đ.án)

Chia sẻ: Nguyễn Lê Huy | Ngày: | Loại File: PDF | Số trang:7

Thêm vào BST

Báo xấu

709
lượt xem 146
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Nhằm giúp các bạn học sinh có tài liệu ôn tập những kiến thức cơ bản, kỹ năng giải các bài tập Toán nhanh nhất và chuẩn bị cho kì thi sắp tới tốt hơn. Hãy tham khảo 2 đề thi học kì 2 Toán 10 kèm đáp án.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: 2 đề thi HK2 Toán 10 - (Kèm Đ.án)

SỞ GD&ĐT BẮC GIANG ĐỀ KIỂM TRA HỌC KÌ II NĂM HỌC 2010-2011 MÔN TOÁN LỚP 10 (ĐỀ CHÍNH THỨC) Thời gian làm bài : 90 phút (Không kể thời gian phát đề) A. PHẦN CHUNG CHO TẤT CẢ HỌC SINH (8 điểm). Câu I. (3 điểm) Giải các bất phương trình sau: x 2 - 3x + 2 1. x 2  5x  4  0 ; 2. >0 x+4 Câu II. (1 điểm) Điều tra tuổi của 30 công nhân của một xưởng may, ta có bảng phân bố tần số sau: Tuổi 20 24 26 30 32 35 Cộng Tần số 3 5 6 5 6 5 30 Tìm độ tuổi trung bình của 30 công nhân, (chính xác đến hàng phần nghìn). Câu III. (3 điểm) Trong mặt phẳng với hệ toạ độ Oxy, cho hai điểm A(2;1), B(-2; 4) và đường thẳng x  2  t d: (t  ) .  y  1  2t 1. Lập phương trình tổng quát của đường thẳng  đi qua hai điểm A, B. 2. Tìm toạ độ điểm H là hình chiếu của điểm B trên đường thẳng d. 3. Lập phương trình đường tròn có tâm nằm trên đường thẳng d đồng thời tiếp xúc với trục hoành và đường thẳng  . Câu IV (1 điểm) 2 2 2 Cho ba số dương a, b, c thỏa mãn hệ thức    1. a 2 b2 c2 Tìm giá trị nhỏ nhất của biểu thức P  abc B. PHẦN RIÊNG - PHẦN TỰ CHỌN (2 điểm). Học sinh chỉ được làm một trong hai phần (phần I hoặc phần II) I. Dành cho học sinh học theo chương trình chuẩn: Câu Va. (1 điểm) 1  Tìm các giá trị lượng giác của góc  , biết cos   ,   ( ;0) . 4 2 Câu VIa. (1 điểm) Tìm tham số m để phương trình sau có nghiệm : 2x 2  2x  m  3  x  1 . II. Dành cho học sinh học theo chương trình nâng cao: Câu Vb. (1 điểm) Cho góc lượng giác  thoả mãn cos  0, sin   0 và tan   cot   4 . Tính giá trị của biểu thức T  tan 4   cot 4  . Câu VIb. (1 điểm) Tìm tham số m để bất phương trình x 2  2x  m  3  0 nghiệm đúng với mọi x thuộc (2; ) . ---------------- Hết ------------------ Họ tên thí sinh:............................................................Số báo danh:.................
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KÌ II NĂM HỌC 2010-2011 MÔN TOÁN, LỚP 10. Chú ý : Dưới đây chỉ là sơ lược từng bước giải và cách cho điểm từng phần của mỗi bài. Bài làm của học sinh yêu cầu phải chi tiết ,lập luận chặt chẽ. Nếu học sinh giải cách khác đúng thì chấm và cho điểm từng phần tương ứng. Câu Nội dung Điểm I (3đ) 1) x2  5x  4  0  1  x  4 1,00 Tập nghiệm của BPT là S = 1; 4 0,5 2) x 2 - 3x + 2 Xét dấu f(x) = x+4 2 0,25 Ta có x - 3x + 2  0  x  1; x  2 x  4  0  x  4 Bảng xét dấu: x - -4 1 2 + 0,75 x 2  3x  2 + | + 0 - 0 + x+4 - 0 + | + | + f(x) - || + 0 - 0 + Từ bẳng xét dấu ta có tập nghiệm của BPT là :S =  4;1   2;   0,5 II (1 đ) Độ tuổi trung bình của 30 công nhân là : 20.3  24.5  26.6  30.5  32.6  35.5 0,75 T 30  28, 433 0,25 III 1)  (3đ) AB   4;3 0,25   Đường thẳng  đi qua hai điểm A, B nên  có một VTCP AB   4;3    có một  0,25 VTPT là n   3; 4   Vậy đường thẳng  đi qua A(2 ;1) và có một VTPT n   3; 4  , có phương trình tổng 0 ,5 quát là : 3  x  2   4  y  1  0  3 x  4 y  10  0  2) đường thẳng d có một VTCP là : u  1; 2  0,25  H  d  H  2  t ;1  2t   BH   4  t; 3  2t  0,25   H là hình chiếu của B trên d  BH .u  0  t  2  H (0;5) 0,5 3) Giả sử đường tròn (C) cần tìm có tâm I và bán kính R 0,25 Do I  d  I  2  t ;1  2t  đường tròn (C) tiếp xúc với trục hoành và tiếp xúc với   d  I ,ox   d  I ,  0,25
t  1  1  2t  t   1 t   3 2 Với t = 1 thì I(3 ;-1) và R =1 . Phương trình đường tròn (C) là :  x  3   y  1  1 2 0,25 1  7 1 1 0,25 Với t= thì I  ;  và R  , Phương trình đường tròn (C) là : 3  3 3 3 2 2  7  1 1 x   y    3  3 9 IV 2 2 2 2 2 c (1 đ) Ta có:   1    0,25 a2 b2 c2 a 2 b2 c2 Do a, b,c là các số dương nên a+2, b+2, c+2 là các số dương Theo côsi cho hai số dương ta có: 2 2 2 2 c 4  2 .   (1) a2 b2 a2 b2 c2  a  2  b  2  0,25 b 4 a 4 TT:  (2) ;  (3) 0,25 b2  a  2  c  2  a2  c  2  b  2  Từ (1) , (2), (3) ta có P = abc  64 , dấu ‘=’ xảy ra khi a=b=c= 4 Vậy Min P = 64 khi a=b=c=4 0,25 Va.    0,25 (1 đ) do     ;0   sin   0  2  15 15 0,25 Ta cã sin 2   cos 2   1  sin 2   1  cos 2    sin    16 4 sin  0,25 tan     15 cos   15 0,25 cot   15 VIa x 1  0 x  1  (1 đ) 2x 2  2x  m  3  x  1 (1)   2 2   2  2 x  2 x  m  3   x  1   x  4 x  4  m (2) 0,5 PT(1) có nghiệm khi và chỉ khi PT (2) có nghiệm thuộc 1;   Số nghiệm của phương trình (2) bằng số giao điểm của đồ thị hàm số y  x 2  4 x  4 và đt có pt : y = -m 0,25
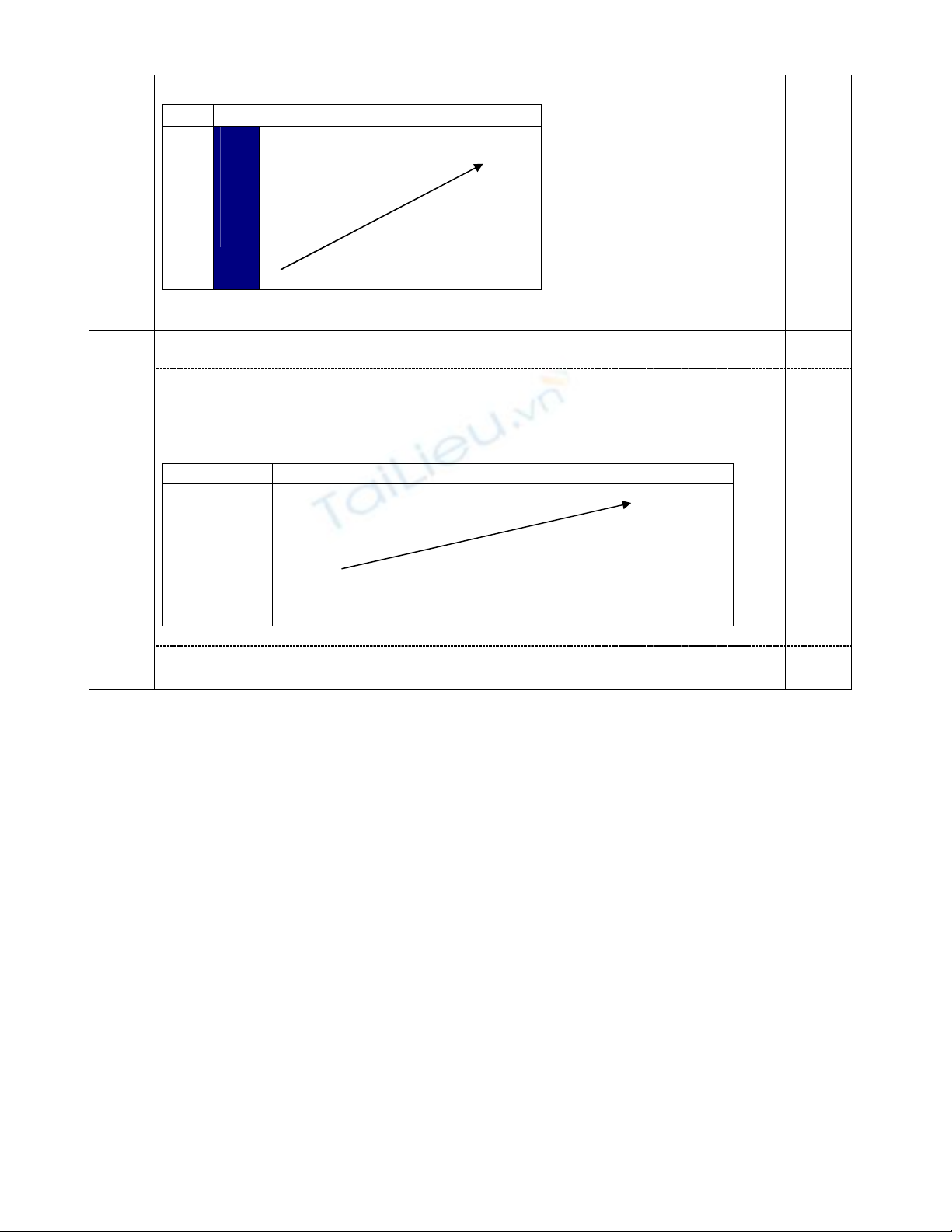
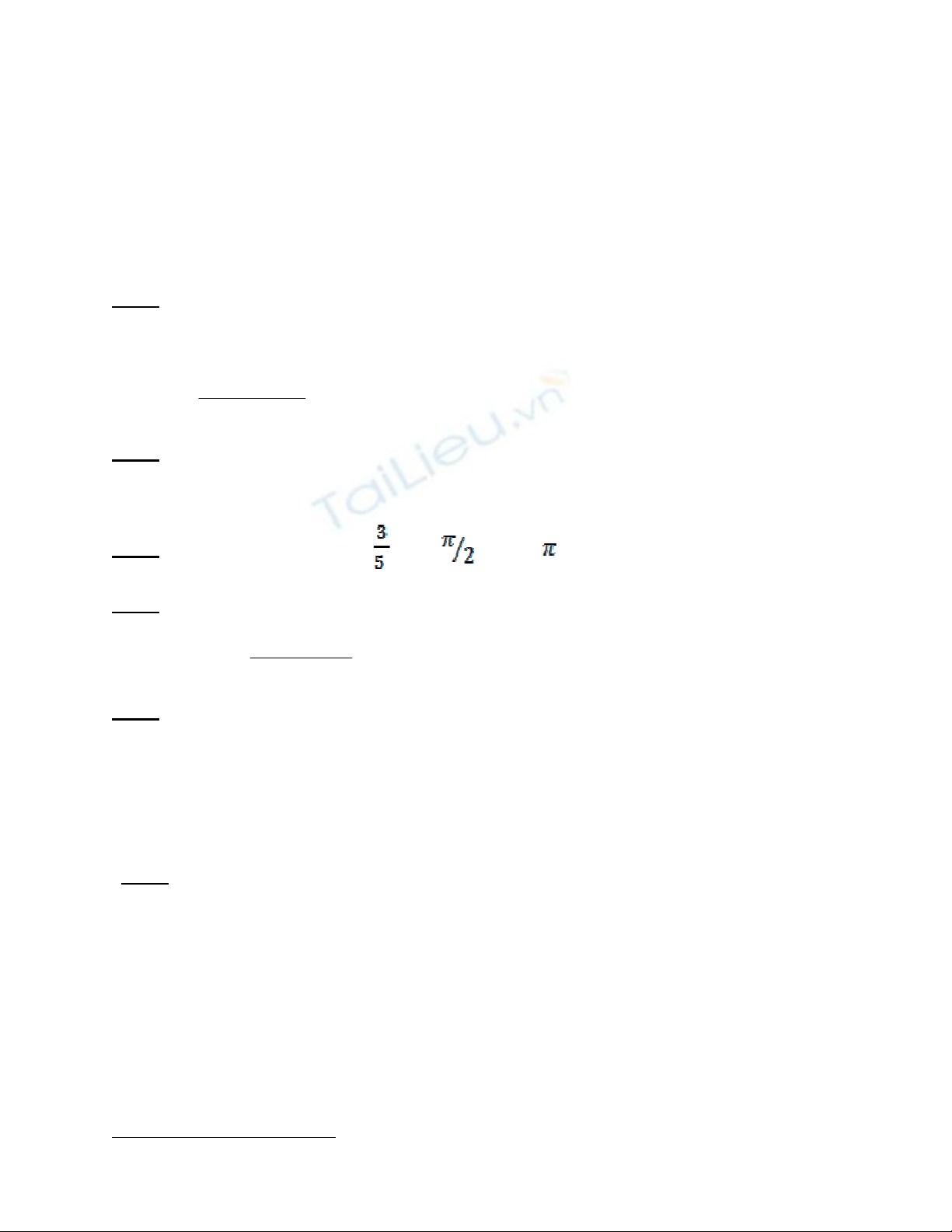
BBT của hàm số y  x 2  4 x  4 trên 1;   0,25 x 1   f(x) 1 Từ BBT ta có thì phương trình có nghiệm  m  1  m  1 Vb 2 0,5 (1 đ)  T  tan 4   cot 4   tan 2   cot 2   2 2 2 0,5   tan   cot    2   2  196  2  194   VIb +Ta có x  2x  m  3  0  x 2  2x  3   m 2 0,25 (1 đ) +Xét BBT của hàm số y  x 2  2x  3 trên  2;   0,5 x 2 + + f(x) 5 Từ BBT ta có 5   m  m  5 là giá trị cần tìm 0,25
SỞ GIÁO DỤC VÀ ĐÀO TẠO TPHCM TRƯỜNG THPT ĐÔNG Á ĐỀ KIỂM TRA HỌC KỲ 2 Môn Toán – lớp 10 Thời gian làm bài: 90 phút (không kể thời gian phát đề) Câu 1 ( 3 điểm ) Giải các bất phương trình sau. a) (x-2)( x 2 +5x +6 ) > 0  2x 2  7 x  7 b)  1 x 2  3x  10 Câu 2 ( 1 điểm ).Tìm các giá trị của m để bất phương trình: x2 – m x – 3m -1 > 0 Câu 3 (1,5 điểm ) Biết cos  =  và (
ĐÁP ÁN TOÁN10 CÂU Ý NỘI DUNG ĐIỂM 1 a (x-2)( x 2 +5x +6 ) > 0 x-2=0  x = 2 0.25đ x 2 +5x +6 = 0  x = -2; x = -3 0.25đ Lập bảng xét dấu đúng 0.5đ S=(-3;-2)  ( 2;+∞) 0.5đ b 0.5đ  2x 2  7x  7  x 2  4x  3  1  2 0 x 2  3 x  10 x  3x  10 0.5đ Lập bảng xét dấu đúng 0.5đ S=( - ∞; -2)  [1;3]  (5; +∞) 2 x2 – m x – 3m -1 > 0 x  R 0.5đ ∆ = m 2 +4(3m+1) < 0 0.5đ m (-6- 32 ; -6+ 32 ) 3 sin 2 α +cos 2 α=1  sin 2 α = 1- cos 2 α 2 2  3  16 sin α = 1-    = 0.25đ  5 25 4 sin 2 α =  5 4 vì (
4 4 7 2 0.5đ 2 cos2α = 1 - 2 sin α = 1 – 2   = - a 5 25 5 cos a  cos 7a Chứng minh rằng:  tan 4a sin 7a  sin a 0.25đ+0.25đ 2 sin 4a. sin 3a b VT =  tan 4a ( VT=VP  đpcm) 2 cos 4a. sin 3a 0.25đ BC (2;-5)  n BC = (5;2) 0.25đ phương trình cạnh BC: 5x + 2y- 13 = 0 c 0.25đ+025 phương trình cạnh BM: x+ y – 5 = 0 Đường thẳng (d) đi qua trọng tâm G và vuông góc với BC , 0.25đ nhận BC làm véc tơ pháp tuyến BC (-2;5) 0.25đ (d) :6x-15y + 5= 0 d 0. 5đ 5.6  2.2  13 21 AH= d(A;BC)=  52  22 29 0.5đ BC= 29 1 21 21 S ∆ABC = . 29  6 2 29 2 phương trình đường tròn (c) đi qua 3 điểm A,B,C là. 0.25đ 43 27 32 0.25đ (c) : x 2  y 2  x y 0 7 7 7 x2 y2 0.25đ+0.25đ Phương trình chính tắc của elip (E):  1 a2 b2 0.25đ F2 (2;0)  c =2 . 0.25đ MF1  MF2  2 a  4 2  32 + 32 =2a  a = 4 0.25đ a 2 +b 2 = c 2  b 2 = a 2 - c 2  b 2 =16 -4 =12 x2 y2 0.25đ phương trình ( E) :  1 16 12