1
Anten và truyn sóng
ThS. Phm Minh Nam
2
Tài liu tham kho
Lê Tin ThưngTrn Văn Sư ,Truy n sóng và
Anten, NXB ð*i h+c Qu.c Gia TPHCM –2010
Constantine A.Balanis, Antenna theory analysis
and design, John Wiley & Son.Inc.,1997.
David M. Pozar, Microwave Engineering, John
Wiley & Son.Inc, 1998
3
Chương trình môn h+c
Phn 1
Chương 1: LHch sI phát triLn anten
Chương 2: Mô t các ñNc tính bQc x* cSa anten
Chương 3: Lí thuyt anten
Chương 4: H th.ng bQc x*
Chương 5: Các lo*i anten
Phn 2
Chương 1: Truy n sóng vô tuyn
Chương 2: Truy n sóng ñưng dây dWn
Chương 3: Truy n sóng .ng dWn sóng
Chương 4: Truy n sóng qua cáp quang
4
ðánh giá
TiLu luYn
Hình thQc làm ngoài gi
Thi gian 3 tun
Thi giZa kỳ
Hình thQc thi t\ luYn
Thi gian thi 60 phút
Thi cu.i kỳ
Hình thQc thi t\ luYn
Thi gian thi 60 phút
5
Chương 1 Lch sphát trin Anten
ThS. Phm Minh Nam
6
Lch sphát trin Anten
Anten là h th.ng cho phép truy n và nhYn
năng lư`ng trưng ñin ta.
Anten có thL ñư`c xem như thit bH dùng ñL
truy n năng lư`ng trưng ñin ta giZa máy
phát và máy thu mà không cn bct kỳ phương
tin truy n dWn tYp trung nào như cáp ñdng,
.ng dWn sóng hoNc s`i quang…
Anten ñư`c ưa chufng trong vic chuyLn ti
các trưng ñin ta g tn s. cao.
7
Lch sphát trin Anten
Các sóng trưng ñin ta chi ph.i ho*t ñfng cSa
Anten ñư`c dihn t bgi h phương trình Maxwell
(1876).
H phương trình Maxwell ñã th.ng nhct các ñHnh luYt
trưlc ñó như Ampere, Faraday…
1886: Heinrich Hertz kiLm chQng ñư`c s\ tdn t*i
sóng ñin ta.
1897: Alexander Popov phát triLn tuyn Anten thYt
ñu tiên có kh năng truy n xa 3 dNm.
8
Lch sphát trin Anten
1901: Guglielmo Marconi ñã hin th\c ñư`c thông tin
vô tuyn xuyên ð*i Tây Dương.
1916: Ln ñu tiên sI dnng ñi u biên ñL truy n tín
hiu ting nói.
1934: T*o ra h th.ng vô tuyn thương m*i ñu tiên
giZa Anh và Pháp ho*t ñfng g 1.8G
19401945: Phát triLn Anten dùng trong radar, Anten
phn x*, Anten thcu kính, Anten dãy…
Hin nay Anten ñư`c sI dnng trong nhi u lĩnh v\c
khác nhau như GPS, WLAN…
9
Chương 2 Các đc tính ca Anten
ThS. Phm Minh Nam
10
C
Cá
ác đ
c đ
c t
c tí
ính c
nh c
a Anten
a Anten
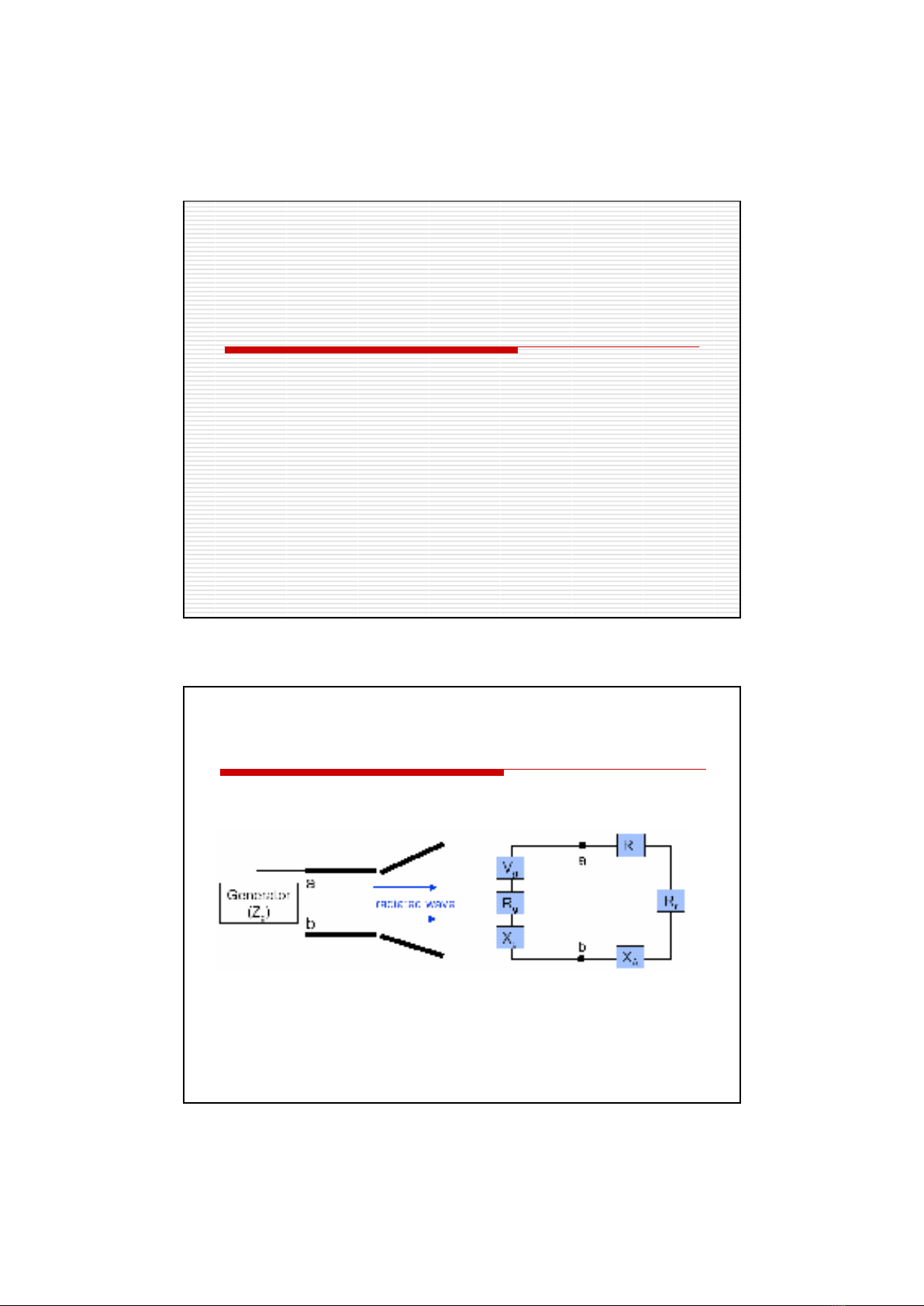
Trkháng vào ca Anten
Xem Anten như m*ng mft cIa
Trg kháng vào: Z
A
= R
A
+ jX
A
Thông thưng R
A
gdm 2 thành phn
+ R
r
là ñin trg bQc x*
+ R
L
là ñin trg tiêu hao cSa Anten