zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Khoa Học Tự Nhiên

Bài giảng Vật lý đại cương 2 - Chương 1: Trường điện từ

Chia sẻ: Hứa Tung | Ngày: | Loại File: PDF | Số trang:32

Báo xấu

53
lượt xem 6
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Vật lý đại cương 2 - Chương 1: Trường điện từ có nội dung trình bày về: luận điểm thứ nhất - điện trường xoáy, luận điểm thứ hai - dòng điện dịch, trường điện từ và hệ phương trình Maxwel. Mời các bạn cùng tham khảo chi tiết nội dung bài giảng.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Vật lý đại cương 2 - Chương 1: Trường điện từ

Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phát biểu luận điểm thứ nhất Phương trình Maxwell-Faraday
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phát biểu luận điểm thứ nhất Mọi từ trường Phương biến thiên theo thời gian đều xuất trình Maxwell-Faraday hiện điện trường xoáy.
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phát biểu luận điểm thứ nhất Phương trình Maxwell-Faraday
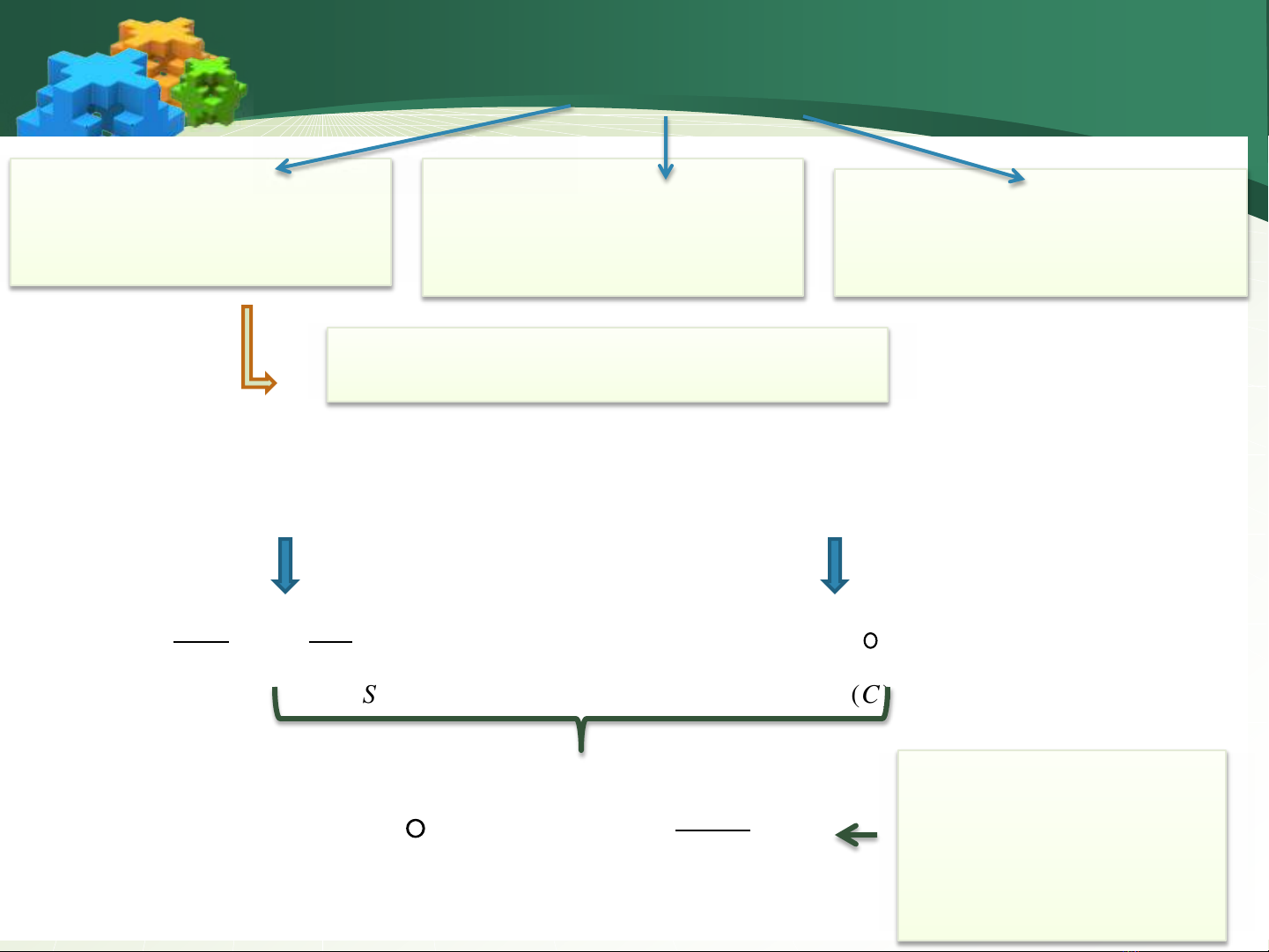
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phương trình Maxwell-Faraday Xét một mạch dẫn kín (C) đặt trong từ trường biến thiên. Sức điện động cảm ứng có thể xác định bằng hai cách sau: d d     c      BdS  c   Edl dt dt S (C )    B  Phương trình  Edl    t dS Maxwell-Faraday (C ) S dạng tích phân
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phương trình Maxwell-Faraday Có thể viết phương trình Maxwell-Faraday dạng vi phân dựa vào định lý Stokes như sau:      B   (C ) Edl   rotEdS    S S t dS Theo định lý Stokes   B Phương trình Maxwell-Faraday rotE   dạng vi phân t
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phát biểu luận điểm thứ hai Biểu thức của mật độ dòng điện dịch Phương trình Maxwell-Ampere
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phát biểu luận điểm thứ hai Biểu thức của mật độ dòng điện dịch Phương trình Maxwell-Ampere
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phát biểu luận điểm thứ hai Mọi điện trường biến thiên theo thời gian đều xuất hiện một từ trường biến thiên
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phát biểu luận điểm thứ hai Biểu thức của mật độ dòng điện dịch Phương trình Maxwell-Ampere
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Biểu thức của mật độ dòng điện dịch Xét hai bản tụ điện có diện tích S và có tích điện tích mặt trên bề mặt bản tụ. Theo định lý Gauss ta có:   dD d   Q  DdS  Q (S ) dt  dt S dD 1 dQ idich  DdS  dS (S )  dt  S dt  S  jdich (S )   dD - mật độ dòng điện dịch D   jdich  dt
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phát biểu luận điểm thứ hai Biểu thức của mật độ dòng điện dịch Phương trình Maxwell-Ampere
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phương trình Maxwell-Ampere Theo như phần trên thì dòng điện toàn phần phải bao gồm dòng điện dẫn và dòng điện dịch. Như vậy định luât Ampere theo điều chỉnh của Maxwell sẽ như sau:        mà jtotal  jdan  jdich  Hdl  I total   jtotaldS    D  (l ) (S ) và jdan  E; jdich  t     D   - Phương trình Maxwell- (l ) Hdl  (S )  jdan  t dS Ampere dạng tích phân
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Phương trình Maxwell-Ampere Có thể viết phương trình Maxwell-Faraday dạng vi phân dựa vào định lý Stokes như sau:       D    Hdl   rotH .dS  ( S )  jdan  t dS (l ) (S ) Định lý Stokes Định luật Maxwell-Ampere    D - Phương trình Maxwell- rotH  jdan  t Ampere dạng vi phân
Ví dụ: mật độ dòng điện Điện trường trong một tụ điện phẳng có dạng E  E0 sin(t ) với E0, tần số f, khoảng cách giữa hai bản d, điện dung của tụ điện C là các đại lượng đã biết. Tìm: 1. Giá trị cực đại của dòng điện dịch. 2. Độ dẫn điện. Biết giá trị cực đại của dòng điện dịch bằng một nửa giá trị cực đại dòng điện dẫn.   jdan  E   S Cd  idich  jdich S jdan  0      D E jdich  t idichmax  0.5idanmax   D   0E      jdichmax S  0.5 jdanmax S idichmax  2CdE0f    jdanmax  2 jdichmax
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Trường điện từ Hệ phương trình Maxwell
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Trường điện từ Hệ phương trình Maxwell
Trường điện từ Luận điểm thứ nhất: Luận điểm thứ hai: Trường điện từ và hệ Điện trường xoáy Dòng điện dịch phương trình Maxwell Trường điện từ Từ hai luận điểm nêu trên của Maxwell có thể đưa ra kết luận là từ trường biến thiên làm xuất hiện điện trường biến thiên VÀ điện trường biến thiên thì sinh ra từ trường biến thiên. Do đó mà trường điện E và trường từ B lan truyền trong không gian dưới dạng sóng, gọi là sóng điện từ. Trường điện từ có mang năng lượng.
Trường điện từ Sóng trường điện từ Xét môi trường truyền sóng trong chân không hoặc điện môi. Q=0 Q  .V    0. Độ dẫn điện   0.      divD   divD  0 rot.rotE   rotB t       rot.rotE  .divE   E   E 2 divB  0 divB  0 2       D E  B  B rotB  0 .rotH  0   0 0 rotE   rotE   t t t t Đặt v2  1     D  D  0 0 rotH  E  rotH  t t   1  E 2 Phương trình truyền sóng cho điện trường 2 E  2 0 v t 2   1  B 2 Phương trình truyền sóng cho từ trường 2 B  2 v t 2 0
Trường điện từ 1 Xét vận tốc truyền sóng v  0 0 1 1 1    3.108 m / s  c  0 0 1 1 4 .10 7 4 .9.109 9.1016 c Vậy v  Trong đó c là vận tốc ánh sáng trong chân không. Như vậy ánh sáng cũng có tính chất điện từ. Đặt n   , n gọi là chiết suất tuyệt đối của môi trường. Do n>1 nên vận tốc truyền sóng điện từ trong môi trường khác chân không có: c c v  c  n
Trường điện từ Sóng điện từ đơn sắc phẳng Sóng điện từ được gọi là đơn sắc phẳng nếu thỏa mãn các điều kiện sau. 1. Sóng điện từ là sóng ngang chỉ phụ thuộc vào một tọa độ. 2. Cả điện trường và từ trường đều vuông góc với phương truyền sóng và tạo thành tam diện thuận như sau:   E  H  phuong truyen song 3. Điện trường và từ trường dao động cùng pha, và trị số thỏa mãn phương trình:    0 E  0 H

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.