BÀI 1: LÀM QUEN VỚI MATLAB
I- Lý thuyết và thực hành
1- mở 1 hàm m-file và thực hiện yêu cầu sau:
a- tạo ma trận có chiều dài n x m:
b- cộng trừ nhân chia hai ma trận vừa tạo( đưa ra kết quả)
c- trích ra đường chéo của 2 ma trận ban đầu sau đó ghép lại thành 1 ma trận mới
d- trích 2 dòng đầu của ma trận 1 và 2 dòng cuối của ma trận 2. sau đó ghép chúng
thành ma trận mới
e- trích cột cuối của ma trận thứ nhất và cột đầu của ma trận 2. sau đó ghép với ma
trận 1 để tạo ma trận mới
% chương trình thực hiện
>> a=[2 4 6 0 ;3 5 7 7;10 4 5 4];
>> b=[2 4 6 1; 4 9 2 4 ;1 5 6 7 ];
>> x=a+b
x =
4 8 12 1
7 14 9 11
11 9 11 11
>> y=a-b
y =
0 0 0 -1
-1 -4 5 3
9 -1 -1 -3
>> z=a.*b
z =
4 16 36 0
12 45 14 28
10 20 30 28
>> t=a./b
t =
1.0000 1.0000 1.0000 0
0.7500 0.5556 3.5000 1.7500
10.0000 0.8000 0.8333 0.5714
>> diag(a); % ham co cong dung trich duong cheo cua ma tran
>> diag(b);
>> x1=[diag(a) diag(b)]
x1 =
2 2
5 9
5 6
>> a1=a(1:2,:);
>> b1=a(2:3,:);
>> x2=[a1;b1]
x2 =
2 4 6 0
3 5 7 7
3 5 7 7
10 4 5 4
>> a2=a(:,4);
>> b2=b(:,1);
>> x3=[a2 b2]
x3 =
0 2
7 4
4 1
2- đồ họa
2.1- trong không gian 2D:
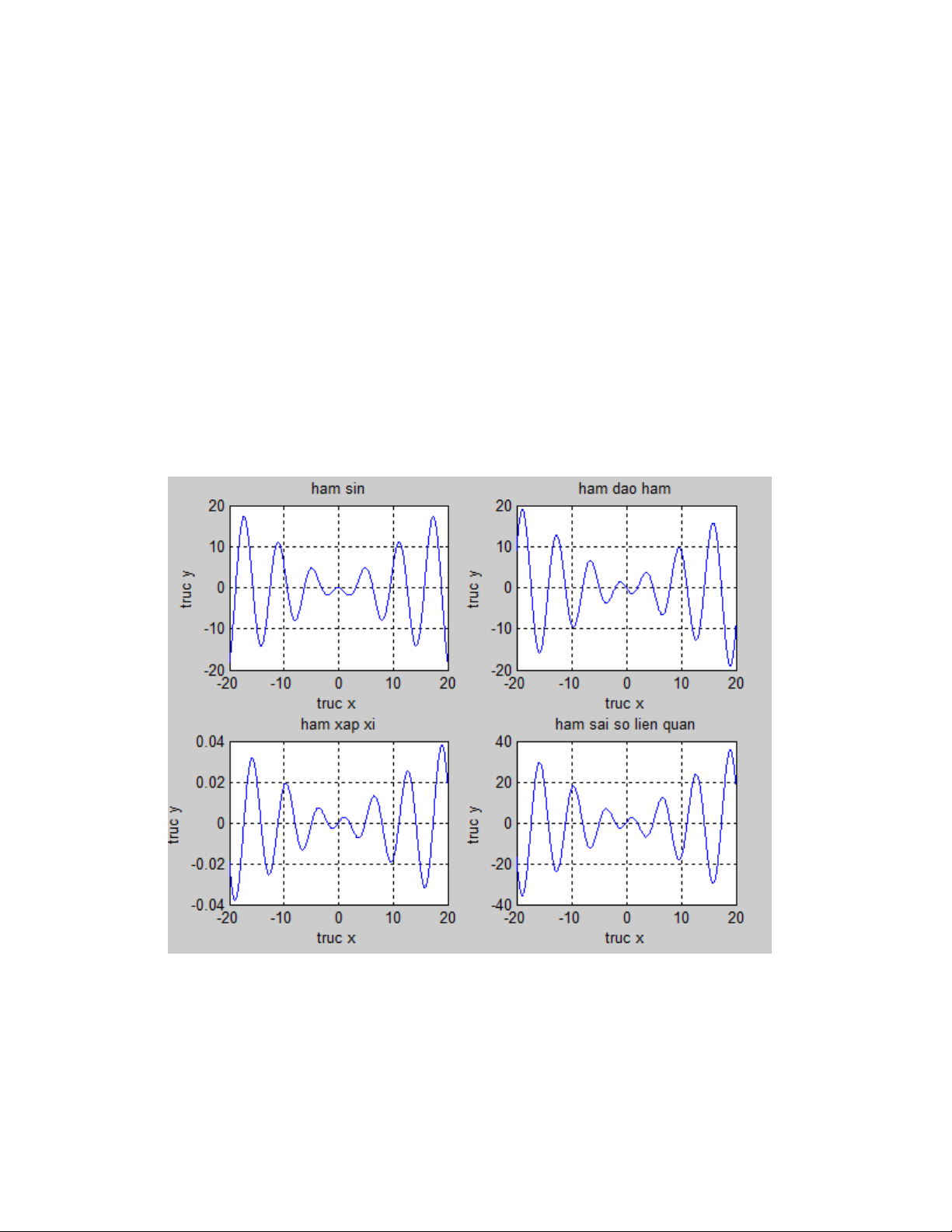
mở 1 hàm m-file và vẽ đồ thị của các hàm sau(vẽ trên cùng 1 của sổ)
hàm f(x) : f(x)= -x.sin(x)
đạo hàm của f(x) : f’(x)=-x.cosx-sinx
đạo hàm xấp xỉ : f12=diff(f(x)/x(2)-x(1))
sai số liên quan: f22=(f12-f’(x)(1:999))/norm(f12)
% chương trình
x=linspace(-20,20,1000); %chon khoang lay mau
%ham f(x);
y=-x.*sin(x);
subplot(2,2,1); % chia o trong do thi
plot(x,y) %ve do thi trong khong gian 2d
grid
title('ham sin'); %tao tieu de cho do thi
xlabel('truc x' ); %tao nhan cho truc x
ylabel('truc y'); %tao nhan cho truc y
%ham dao ham;
y1=-x.*cos(x)-sin(x);
subplot(2,2,2);
plot(x,y1)
grid %ve luoi trong do thi
title('ham dao ham');
xlabel('truc x');
ylabel('truc y');
%ham xap xi
y2=diff(y/x(2)-x(1));
subplot(2,2,3);
plot(x(1:999),y2);
grid
title('ham xap xi');
xlabel('truc x');
ylabel('truc y');
y3=(y2-y1(1:999))/norm(y2);
subplot(2,2,4);
plot(x(1:999),y3);
grid
title('ham sai so lien quan');
xlabel('truc x');
ylabel('truc y');
%ket qua chuong trinh
2.2-trong không gian 3D:
mở 1 hàm m-file và vẽ đồ thị của các hàm sau(vẽ trên từng cửa sổ)
a- z1=f(x,y)=sinx.siny, với x,y=[0,
π
]
b- z2=f(x,y)=x - x3 + y2 + 1, với x,y=[-3,3]
c- z3=f(x,y)=
2 2
2 2
sin( )
( ).
x y
x y x
+
+
, với x,y=[-8,8]
% do thi 1
x=(0:0.05:pi)
y=(0:0.05:pi)
[x,y]=meshgrid(x,y); % tao ma tran he thong trong do thi 3d
z1=sin(x).*sin(y);
figure; %tao them 1 do thi moi
mesh(x,y,z1); %ve do thi 3d
xlabel('Truc x');
ylabel('Truc y');
zlabel('Truc z1');
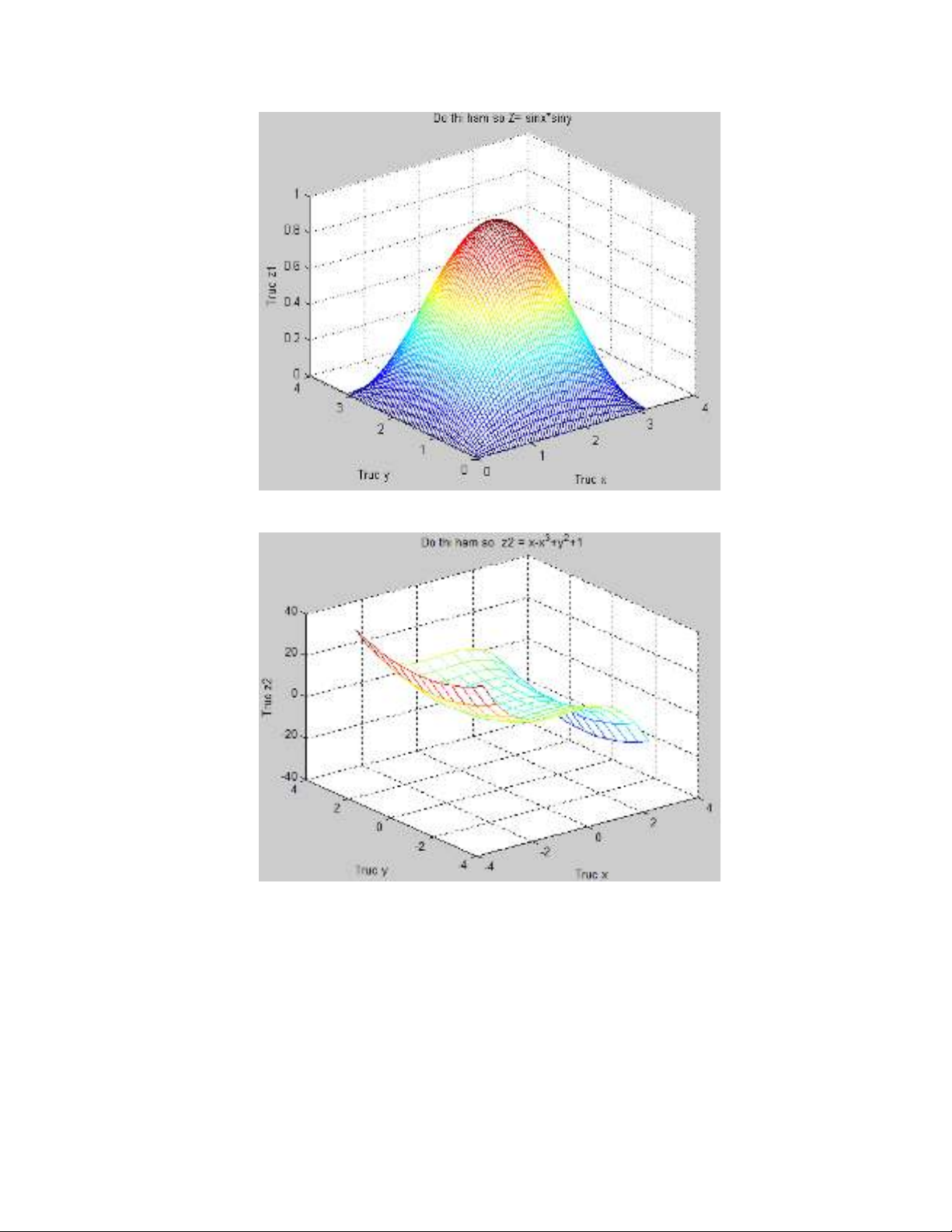
title(' Do thi ham so Z= sinx*siny');
% do thi 2
[x,y]=meshgrid(-3:0.5:3);
z2=x-x.^3+y.^2+1;
figure;
mesh(x,y,z2);
xlabel('Truc x');
ylabel('Truc y');
zlabel('Truc z2');
title(' Do thi ham so z2 = x-x^3+y^2+1');
% do thi 3
[x,y]=meshgrid(-8:0.5:8);
z3=sin (sqrt(x.^2+y.^2))./sqrt((x.^2+y.^2).*x);
figure;
mesh(x,y,z3);
xlabel('Truc x');
ylabel('Truc y');
zlabel('Trucz3');
title(' Do thi ham so z3 = sin((sqrt(x.^2+y.^2)./sqrt((x.^2+y.^2).*x))');
% ket qua chuong trinh