Insertion Sort
•N i dungộ
–Gi i thu tả ậ
–Ví d minh h aụ ọ
–Phân tích th i gian ch yờ ạ
•Tr ng h p x u nh tườ ợ ấ ấ
•Trung bình
•T t nh tố ấ
Insertion Sort
•L u ý quan sát sau đâyư:
–Dãy có 1 ph n t thì đ c s p.ầ ử ượ ắ
–T ng quát : n u ta có dãy đã đ c s p có ổ ế ượ ắ k ph n tầ ử,
ta có th chèn m t ph n t m i đ t o ra m t dãy ể ộ ầ ử ớ ể ạ ộ
đ c s p có kích th c ượ ắ ướ k + 1
Insertion Sort
Ví dụ
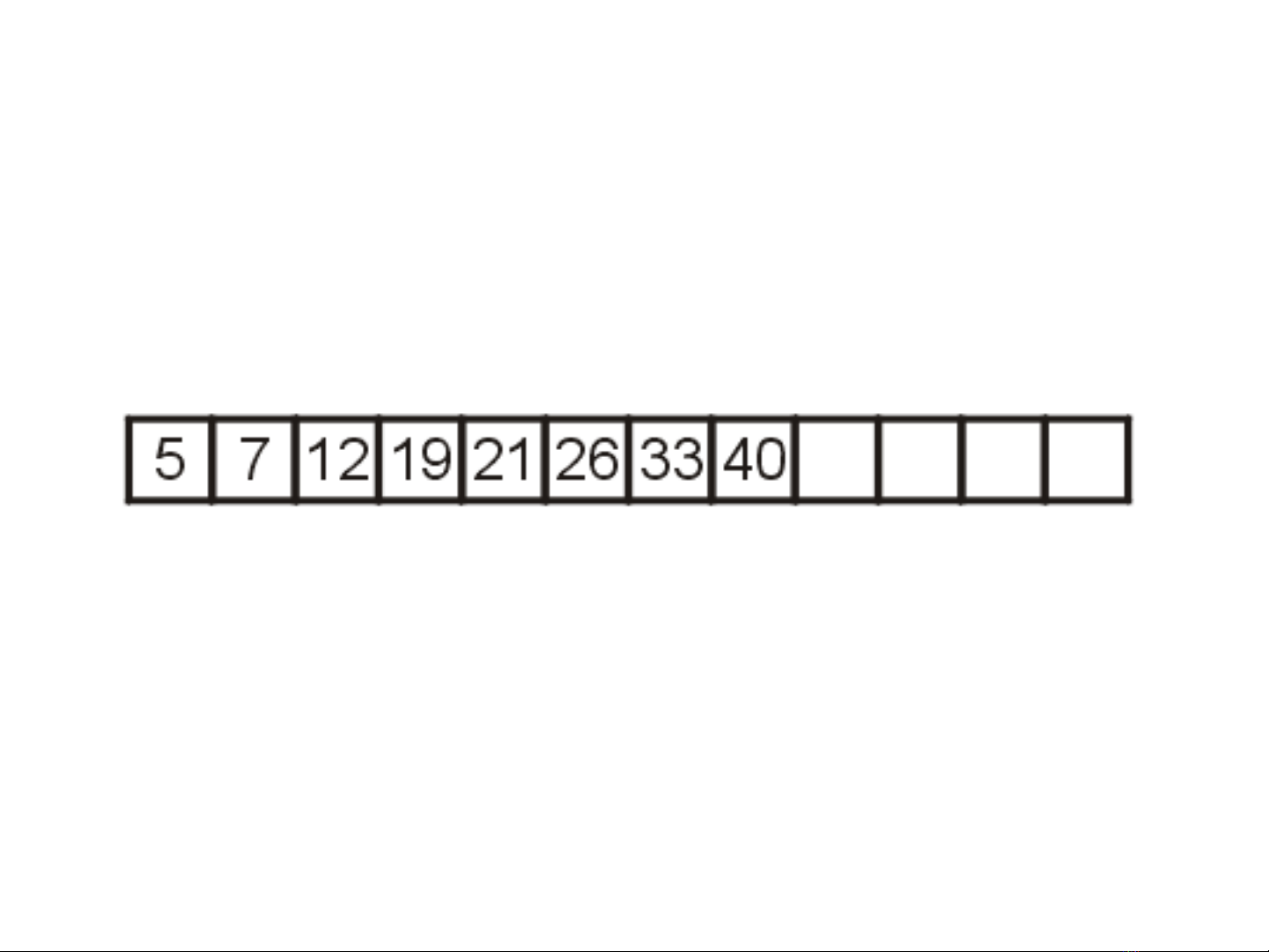
• Hãy xem dãy đ c s p sau đây ch a ượ ắ ứ k = 8 ph n tầ ử
•Gi s ta mu n chèn ph n t 14 vào trong dãy sao ả ử ố ầ ử
cho dãy v n đ c s p.ẫ ượ ắ
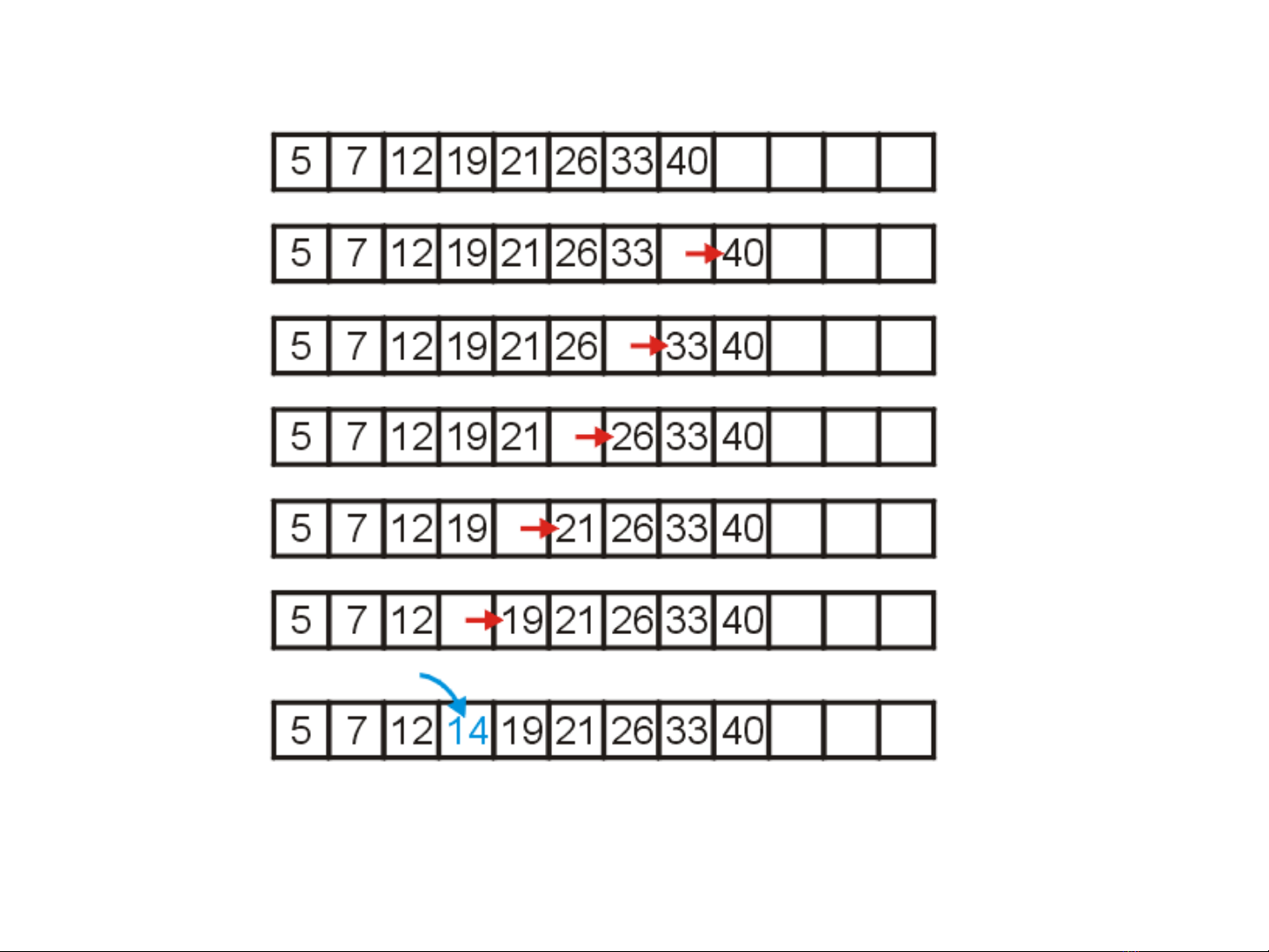
•B t đ u đi t cu i dãy, n u ph n t mang giá tr l n ắ ầ ừ ố ế ầ ử ị ớ
h n 14, copy nó sang ph iơ ả .
Insertion Sort
Khi tìm đ c ph n t có giá tr bé h n 14, chèn 14 vào ượ ầ ử ị ơ
v trí b tr ngị ỏ ố .
Insertion Sort
•V i dãy b t kỳớ ấ :
–Xem ph n t đ u tiên là m t dãy đ c s p có kích ầ ử ầ ộ ượ ắ
th c ướ k = 1.
•Sau đó, gi s ta đã có dãy đ c s p có kích ả ử ượ ắ
th c ướ k.
–Chèn ph n t th (ầ ử ứ k + 1) trong dãy ch a đ c s p ư ượ ắ
vào trong dãy trên.
–Dãy đ c s p bây gi có kích th c ượ ắ ờ ướ k + 1
Gi i thu tả ậ