Ch ngươ 8
GIAO THOA ÁNH SÁNG
Ch ngươ 8
GIAO THOA ÁNH SÁNG
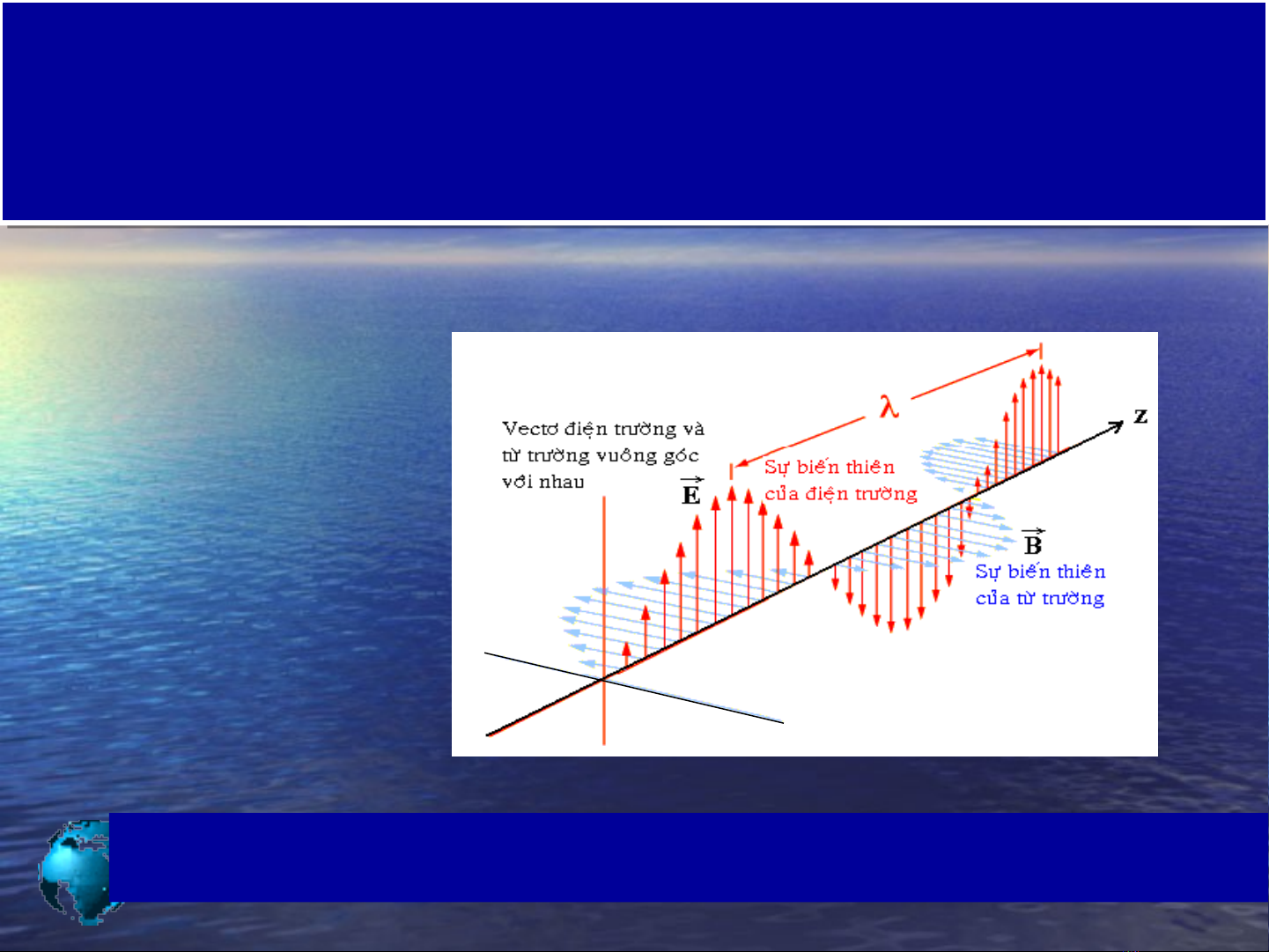
Ánh sáng lan truyền dưới dạng sóng
Hình 8.1: Sóng đi nệ từ
x
Oy
8.1. LÝ
THUY T SÓNG Ế
V ÁNH SÁNGỀ
8.1.1. Các đc ặ
tr ng c a sóng ư ủ
ánh sáng
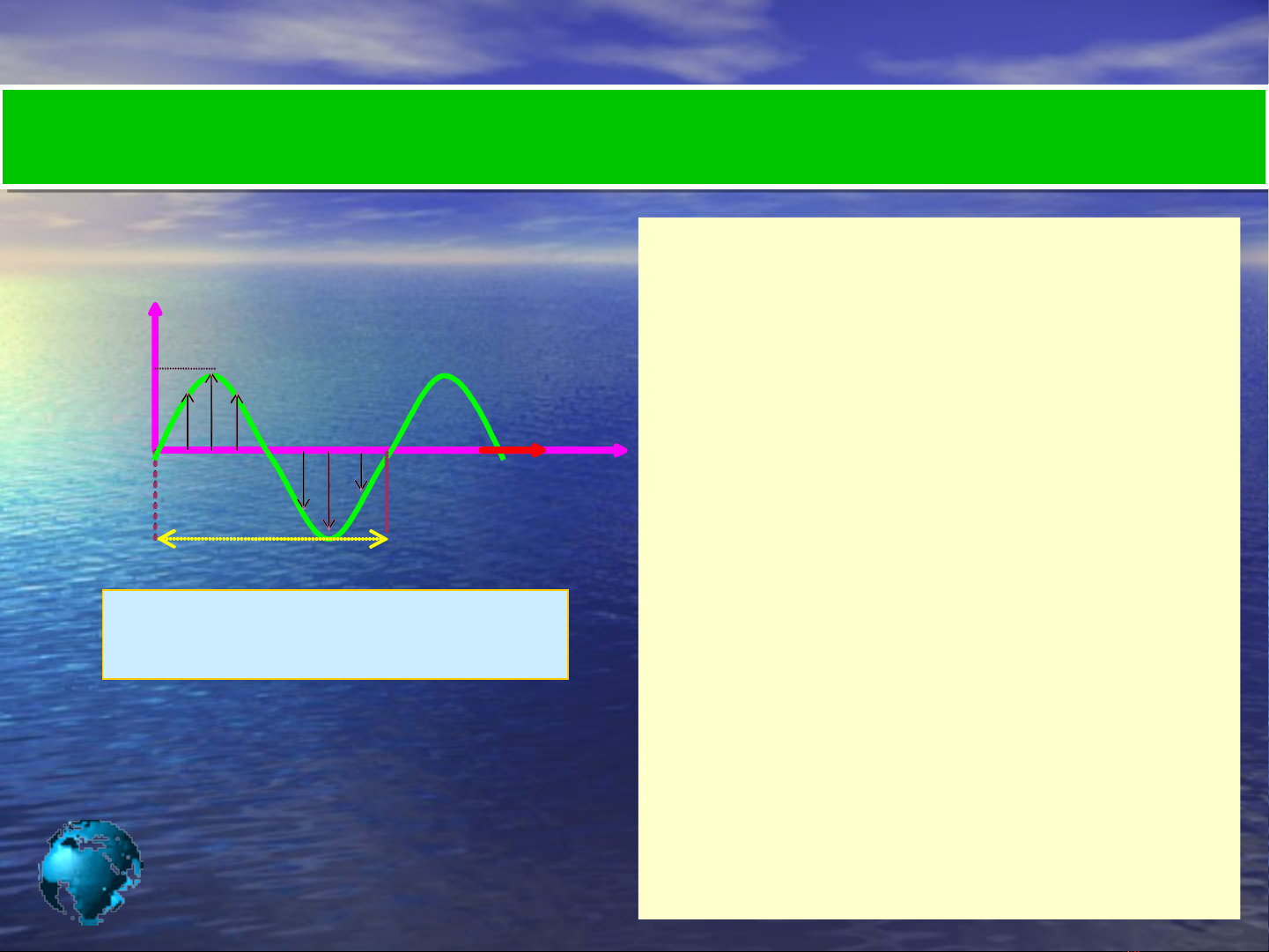
Sóng ánh sáng có các đc tr ng c b n sau:ặ ư ơ ả
Sóng ánh sáng có các đc tr ng c b n sau:ặ ư ơ ả
Dao đng ánhộ sáng
Biên đ sángộ (a)
C ng đ sáng (I = aườ ộ 2)
Chu k dao đng sáng (T)ỳ ộ
T n s sóngầ ố =1/T
T n s gócầ ố = 2/T
B c sóng ánh sángướ =cT
O
a
x
λ
z
-a
c
r
Hình 8.2: Dao đng c a ộ ủ
sóng ánh sáng

8.1.2. Ph ng trình sóng ánh sáng đn s cươ ơ ắ
1. Quang l c a tia sángộ ủ
Quang l c a tia sáng t A đn Bộ ủ ừ ế :
LAB = [AB] = n.l
Xét môi tr ng đng ch t v ph ng di n quang h c ườ ồ ấ ề ươ ệ ọ
có chi t su t không đi là nế ấ ổ , l là kho ng cách t A đn ả ừ ế
B
B
A
I
n1
n2
Hình 8.3: Quang l qua hai môi tr ngộ ườ

Tr ng h p tia sáng truy n t A đn B qua hai ườ ợ ề ừ ế
môi tr ng đng ch t khác nhau.ườ ồ ấ
G i ọl1 là quãng đng ánh sáng đi t A đn I, ườ ừ ế l2 là quãng đng ườ
ánh sáng đi t I đn B.ừ ế
Quang l ánh sáng đi t A đn B là:ộ ừ ế
LAB = LAI + LIB
LAB = n1l1 + n2l2

Tương tự, xét tia sáng đi từ A đến B qua
ba môi trường có chiết suất khác nhau:
LAB = LAI + LIJ + LJB
LAB = n1l1 + n2l2 + n3l3
A
IJ
B
n2
n1
Hình 8.4: Quang lộ qua ba môi trường
Hình 8.4: Quang lộ qua ba môi trường











![Bài tập Vật lý sóng: Tổng hợp bài tập 6 [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250805/oursky04/135x160/401768817575.jpg)














