1
1
CÂN BẰNG PHA HỆ 1 CẤU TỬ
5.1. Khái quát về cân bằng pha trong hệ một cấu tử
5.2. Phương trình Clausius - Clapeyron
5.3. nh hưng của áp suất tổng đến áp suất hơi
bão hòa
5.4. nh hưng của nhiệt độ đến áp suất hơi bão
hòa
5.5 Biểu đồ trạng thái của hệ một cấu tử
CHƯƠNG 5
2
5.1. Khái quát về cân bằng pha
trong hệ một cấu tử
Hêmtcutưl hê ch gmmtcht nguyên cht. Cân
bng pha trong hêmtcutưl cân bng giacctrng
thitphpcamtcht. trng thi khihoclng,hu
htccchtch tntich c mtdng pha. Song chng c
nhiutrng thitphprnkhc nhau gil ccdng đa
hnh hay điviđơn chtgil ccdng thù hnh.
Sư chuyntư trng thitphpny sang trng thitp
hpkhcgil sư chuynpha cahêmtcutư.Sư
chuyn pha bao giơ cng km theo sưthay điđtngt
nhng tnh chtcahênhư khilưng riêng, nhitdung,
thêtch,hiung nhit…
Khi pdng quy tcpha Gibbs cho hêmtcutưta c:
f32f12fkc
3
Nếuhêgồm 1 pha:c = 2. Nghal ca2 thông sôbên ngoi
đuc thêtythay đi trong mtgiihnxcđnh m hê
vntnti 1 pha.
Nếuhêgồm 2 pha nằmcân bằng:c = 1.Nghal trong 2
thông sôbên ngoi, thi ch mt thông sôl đclp, thông sô
cnlil thông sôphu thuc. Nicch khc, mipsut,
nhitđô chuyn pha c giatr phu thucva xcđnh.Ngưc
li, cng c thênipsutchuynpha l hm sô canhitđô
chuynpha.
Nếuhêgồm 3 pha nằmcân bằng:c = 0.nghal ch c thê
tnti cân bng ca 3 pha trong mtđiukinbên ngoihon
tonxcđnh (vê psutva nhitđô). Cng c thê khng
đnh, tuy hêmtcutư c thêtnti nhiudng pha khc
nhau, song sôpha đng thinm trong mttrng thi cân
bng tiđa ch c thêl 3(v đôtưdo c≥0).
5.1. Khái quát về cân bằng pha
trong hệ một cấu tử
4
5.2.1 nh hưng của áp suất đến nhiệt độ
chuyển pha
Đivihêmtcutưthithêđng pch cnphuthuc
vonhit đ và áp sut nên ccđilưng đctrưng cơ
bn cho sư chuynpha l nhit đ và áp sut.Chng c
mi liên hê trctipvinhau trong qu trnh chuynpha
đa đưc Clapeyron - Clausius thitlpbng biuthc:
Trong đo:
T: nhitđô tuytđi.
V: sư bin thiên thêtch capha tothnh va
pha ban đu.
: nhitchuynpha.
V.T
dP
dT
5.2. Phương trình Clausius Clapeyron
2
5
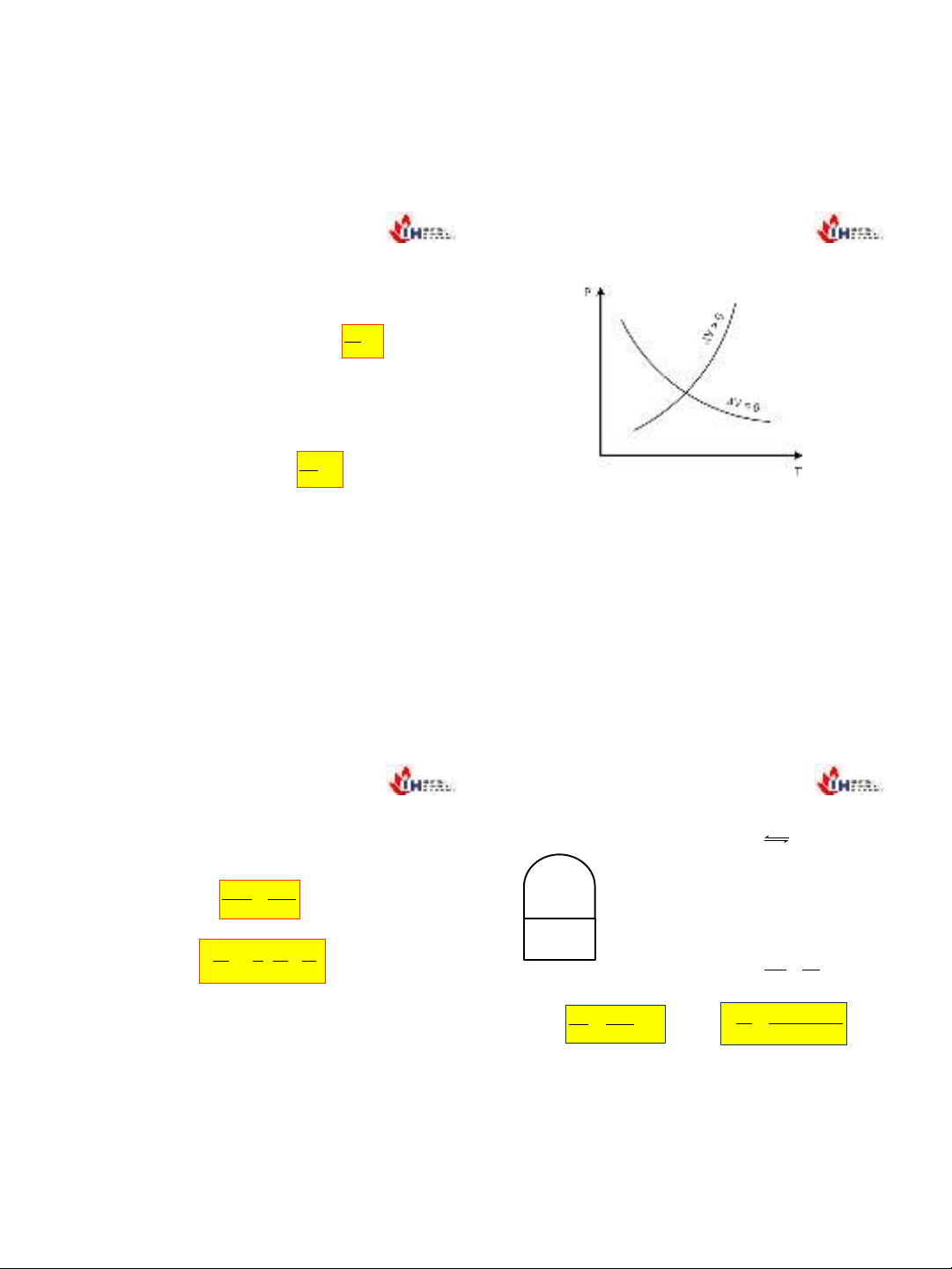
Ta conhnxtsau:
Viqu trnh sôi (hóa hơi):
λhh>0 và ΔV =Vh–Vl>0 nên:
Viqu trnh nng chythicnVcothê dương hoc
âm.đa sô chtthido đo:
0
dP
dT
Nghal khi psuttăng thi nhitđô tăng.Đưng cong P =
f(T) hưng sang phi (hình 5.1). Đây là trưng hp ph
bin ca nhiu nguyên cht.
0
dP
dT
5.2.1 nh hưng của áp suất đến nhiệt độ
chuyển pha
5.2. Phương trình Clausius Clapeyron
6
Hình 5.1. Sự phụ thuộc của nhiệt độ nóng chảy vào
áp suất
5.2.1 nh hưng của áp suất đến nhiệt độ
chuyển pha
7
Phương trnh Clausius - Clapeyron II mô t nh hưng
ca nhit đ đn áp sut hơi bão hòa:
Ta có th rút ra:
Từ phương trình này ta có th tính toán gn đng các
thông s nhit đng như áp sut hơi,nhit đ sôi hay
nhit hóa hơi…
2
RT
dT
dlnP
121
2
T
1
T
1
RP
P
ln
5.2.2 nh hưng nhiệtđôđếnpsuấthơi
bohòa
5.2. Phương trình Clausius Clapeyron
8
Khi h cân bng: Glng Ghơi
Hay dGl=dGh
Khi T = const: dG = V. dP
Nên ta có: Vl.dPl= Vh.dPh
Áp suttcđng lên pha lng chnh l p
suttng cng nên:
5.3. nh hưng của áp suất tổng
cộng đến áp suất hơi bão hòa
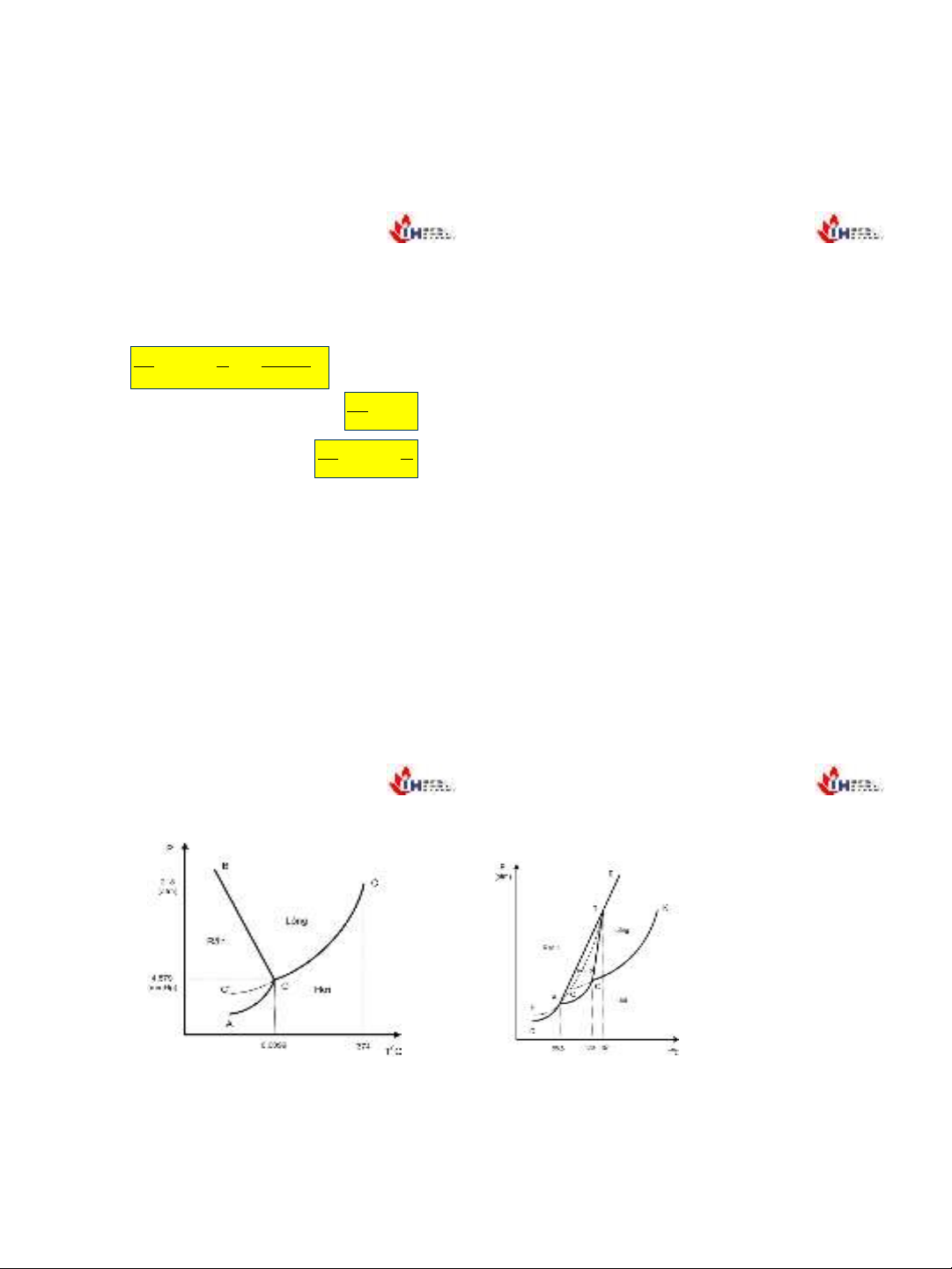
Lỏng A
Hơi A + khí
Pt= P + P’
Xét hệ sau:
h
l
tV
V
dP
dP
T.R
PPV
P
P
ln 1,t2,tl
1
2
Ta chng minh đưc h thc sau:
hay
3
9
Theo Clausius Clapeyron thì nhit chuyn pha tùy thuc vào
áp sut cân bng nên =(T, P)
Ly vi phân từng bin và kt hp PT C–C I ta có:
+Đi vi cân bng L–Hhay R–H, ta có:
+Đi vi cân bng R–L, ta có:
5.4. nh hưng của nhiệt độ đến
nhiệt chuyển pha
P
PT
ΔVln
λ
T
λ
ΔC
dT
dλ
P
ΔC
dT
dλ
T
λ
ΔC
dT
dλ
P
10
Trng thái ca h mt cu tử có th biu diễn bi phương trình
liên h gia các thông s ca h.
Nhưng các h ta thưng gp không ch là h mt pha khí lý
tưng mà là h d th nhiu pha.Nu dùng phương trình trng
thái đ biu diễn mt h như th thì rt phc tp.Do đ ngưi
ta thưng biu diễn trng thái ca h bng các gin đ.
Trng thái ca h đưc hoàn toàn xác đnh bi ba thông s:áp
sut,nhit đ và th tích riêng. Vì th biu đ không gian gm
ba trc thng góc vi nhau, trên đ ghi tương ng các giá tr P,
Tvà V. Nu kho sát trong điu kin 1 thông s nào đ ca h
không đi thì ta có các biu đ phng:
–Khi V = const, ta có biu đ đng tích (P -T).
–Khi P = const, ta có biu đ đng áp (T -V).
–Khi T = const, ta có biu đ đng nhit (P -V).
Tùy theo yêu cu nghiên cu mà ta sử dng nhng biu đ
thích hp. Sau đây chúng ta xét biu đ trng thái (P -T) ca
vài cht đ làm ví d.
5.5. Giản đồ trạng thái của hệ một cấu tử
11
5.5. Giản đồ trạng thái của hệ một cấu tử
5.5.1 Biểu đồ trạng thái của nước
12
•Lưu huỳnh rắn tồn tại dưới hai dạng thù
hình là:dạng trực thoi (dạng rombic: R.1) và
dạng đơn tà (monoclinic: R.2).
•Các đường nét liền trên giản đồ mô tả cân
bằng bền giữa hai pha tương ứng.Những
đường này chia giản đồ thành 4 vùng tương
ứng với 4dạng pha. Điểm Kgọi là điểm tới
hạn.
•Các đường nét đứt mô tả các cân bằng
không bền.
Các điểm A, B và C là các điểm ba bền, mô tả
các cân bằng ba pha tương ứng.
5.5. Giản đồ trạng thái của hệ một cấu tử
5.5.2 Biểu đồ trạng thái củalưu huỳnh
4
13
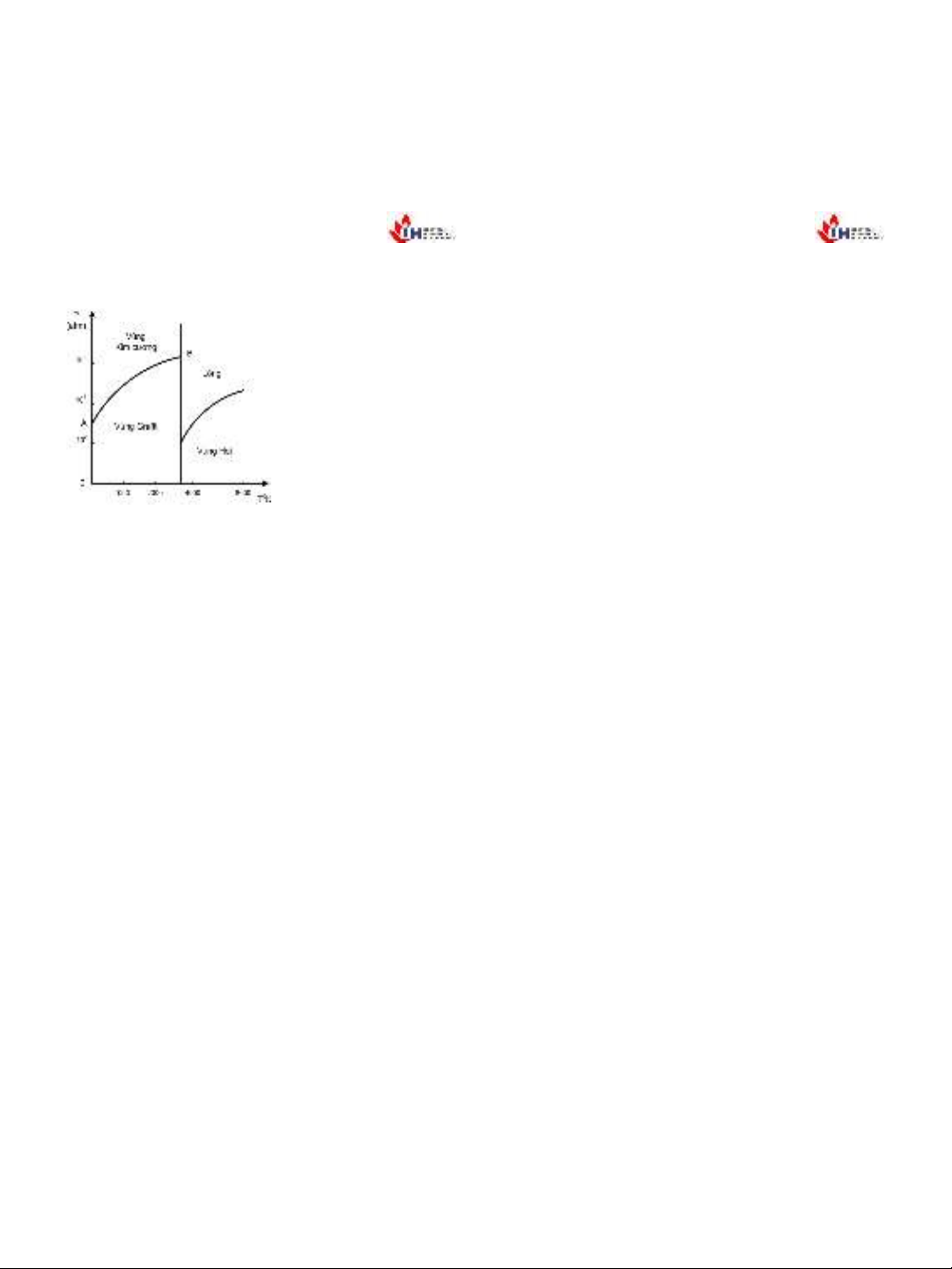
Đường cong AB là đường cân bằng
cacbon dạng kim cương và cacbon dạng
grafit. Về mặt nhiệt động,ở điều kiện bình
thường grafit bền hơn kim cương.Muốn
chuyển hóa grafit thành kim cương ở
2980K thì phải cần áp suất P > 2,2.104atm.
Nhưng trong quá trình thực tế chỉ xảy ra
ở điều kiện nhiệt độ cao, áp suất rất cao và
có xúc tác. Ví dụ ở nhiệt độ 20000C, áp
suất trên 7,1.105atm và có hỗn hợp xúc tác
tantan - coban, người ta có thể tạo được
kim cương từ grafit.
5.5. Giản đồ trạng thái của hệ một cấu tử
5.5.1 Biểu đồ trạng thái của cacbon
14
Bài tp mẫu
Ví dụ 1: Tính áp sut cn thit đ nhit đ sôi ca nưc là
120,90C. Bit nhit hóa hơi ca nưc 538,1 cal/g.
Ví dụ 2: 00Cnhit nóng chy ca nưc đ là 5996,63 J/mol,
th tích riêng ca nưc lng và nưc đ tương ng là Vl=
1,001 cm3/g, Vr= 1,089 cm3/g.Hi khi áp sut 3 atm thì nhit đ
nóng chy ca nưc đ là bao nhiêu?
Ví dụ 4: Xác đnh lưng CS2đưc ly ra khi thi 0,005 m3
không khí vào CS2áp sut 720 mmHg và 400C. Cho bit nhit
hóa hơi ca CS2 nhit đ sôi chuẩn 46,50Clà 355,8 J/g.