1
Chương IV
ðNG LC HC CHT LNG LÝ TƯNG
ðng lc hc cht lng nghiên cu cơ s lý thuyt chuyn ñng ca cht
lng và xây dng các phương trình vi phân mô t' chuyn ñng này trong m)i
quan h+ v,i các ngo-i lc tác d.ng.
Cht lng lý tưng khi b qua s 'nh hưng ca tính nh,t, có nghĩa là h+
s) nh,t
0
=
.
1.PHƯƠNG TRÌNH VI PHÂN CHUY!N ðNG " PHƯƠNG
TRÌNH EULER.
Xut phát t8 nguyên lý bin thiên ñng lư9ng: Ngo-i lc tác d.ng lên mt
h+ th)ng cht lng b<ng t)c ñ thay ñ=i ñng lư9ng ca kh)i cht lng ñó. Ta
có:
1
du
F grad p
dt
ρ
− =
(4.1)
Chiu lên các tr.c tCa ñ, phương trình (1.1) tr thành:
1
1
1
x
x
y
y
z
z
du
p
F
x dt
du
p
F
y dt
du
p
F
z dt
ρ
ρ
ρ
∂
− =
∂
∂
− =
∂
∂
− =
∂
(4.2)
Phương trình (4.1) và (4.2) gCi là phương trình vi phân chuyn ñng Euler ca
cht lng lý tưng d-ng vector và hình chiu tương ng.
2.BÀI TOÁN ðNG LC HC CHT LNG LÝ TƯNG
Trong trưHng h9p cht lng lý tưng, không nén ñư9c, h+ phương trình Euler
có 4 Jn
, ,
x y z
u u u
và áp sut p. ð gi'i h+ phương trình này ta sL d.ng thêm
phương trình liên t.c:
0
y
xz
u
uu
divu x y z
∂
∂∂
= + + =
∂ ∂ ∂
(4.3)
ð tích phân h+ 4 phương trình trên, ta thêm vào ñiNu ki+n ñOu và ñiNu ki+n
biên ca nó:
•ðiNu ki+n ñOu là ñiNu ki+n xác ñPnh các thành phOn vQn t)c và áp sut
t-i thHi ñim ban ñOu t=0:
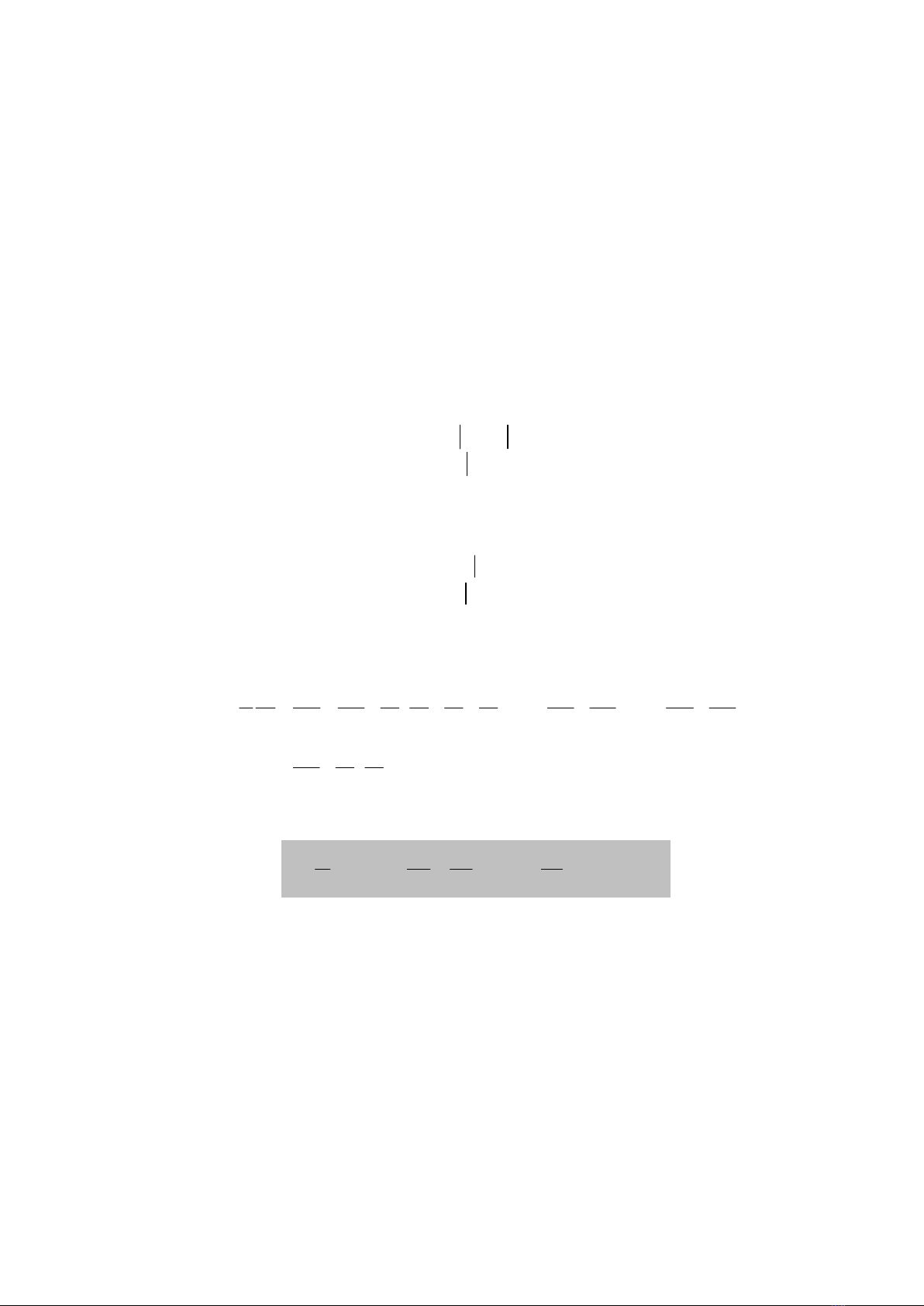
2
(
)
(
)
( ) ( )
( ) ( )
( ) ( )
1
2
3
4
0 , ,
0 , ,
0 , ,
0 , ,
x
y
z
u f x y z
u f x y z
u f x y z
p f x y z
=
=
=
=
(4.4)
•
ðiNu ki+n biên là ñiNu ki+n xác ñPnh biên gi,i môi trưHng lng ñang xét
và biu thP b<ng ñiNu ki+n cho trên mRt vQt và ñiNu ki+n khá xa vQt rSn
(coi
∞
). ðiNu ki+n biên trên mRt vQt rSn ph'i tha mãn ñiNu ki+n h-t
lng không xuyên qua hoRc tách rHi khi mRt vQt rSn.
U
Khi vQt rSn S ñng yên, dòng cht lng lý tưng chuyn ñng t8
vô cùng ñn bao quanh vQt ta có:
0
n n
S S
u v
u
∞
=
=
(4.5)
U
Khi vQt rSn S chuyn ñng trong cht lng lý tưng v,i vQn t)c
v
trong cht lng ñư9c coi là ñng yên  vô cùng, ta có:
0
n S
u
u u
∞ ∞
=
=
(4.6)
3.D+NG LAMB – GROMECO C/A PHƯƠNG TRÌNH EULER
Sau khi sSp xp trên phương x, ta ñư9c
( ) ( )
2
22
2
1
2 2 2
2
y y
x x x x x
z z
x z y
xz y
y z
u u
du u u u u
u u
p
F u u
x dt t x z y x y
uuu rot u u rot u
t x
ρ
∂
∂ ∂ ∂∂
∂ ∂
− = = + + + + − − −
∂ ∂ ∂ ∂ ∂ ∂ ∂
∂∂
= + + −
∂ ∂
(4.7)
Ta bin ñ=i tương t cho phương y và z. Cu)i cùng ta ñư9c d-ng Lamb –
Gromeco ca phương trình Euler:
( )
2
1
2
du u u
F grad p grad rot u u
dt t
ρ
∂
− = = + + ∧
∂
(4.8)
Tính cht ñRc bi+t ca phương trình vi phân chuyn ñng ca cht lng lý
tưng dư,i d-ng Gromeco là tan t-i d-ng hin ca vector xoáy ca vQn t)c.
4.PHƯƠNG TRÌNH BERNOULLI CHO DƯ1NG DÒNG
Trong trưHng h9p t=ng quát, phương trình vi phân chuyn ñng ca cht lng
lý tưng không tích phân ñư9c. ð tích phân ñư9c, ta xét mt s) trưHng h9p
ñRc bi+t.
a.Tích phân Lagrange – Cauchy v=i chuy?n ñAng có thD
Xét cht lng không nén ñư9c, chuyn ñng không xoáy dư,i tác d.ng ca lc
có th, nghĩa là
3
0
const
rot u
u grad
F grad U
ϕ
=
=
=
=
(a)
v,i
ϕ
là hàm th vQn t)c, U là hàm th lc kh)i ñơn vP.
Khi ñó:
( )
ugrad grad
t t t
ϕ
ϕ
∂ ∂ ∂
= =
∂ ∂ ∂
(b)
( )
1
p
gradp grad
ρ ρ
=
(c)
Th (a), (b) và (c) vào phương trình (4.8), ta thu ñư9c
2
0
2
u p
grad U
t
ϕ
ρ
∂
+ + − =
∂
(4.9)
Tích phân (1.9) cho ta
( )
2
2
u p
U C t
t
ϕ
ρ
∂+ + − =
∂
(4.10)
v,i
(
)
C t
xác ñPnh t8 ñiNu ki+n biên.
b.Tích phân Euler
Khi cht lng chuyn ñng d8ng, (4.10) có d-ng
2
2
u p
U Const
ρ
+ − =
(4.11)
Khi lc kh)i là trCng lc,
U gz
= −
, (4.11) tr thành
2
2
u p
z Const
g
γ
+ + =
(4.12)
GCi
2
2
u p
H z
g
γ
= + +
– ñ cao thy lc trong toàn miNn cht lng.
2
2
u
g
– ñ cao ño t)c.
p
γ
– ñ cao ño áp.
z– ñ cao ño mc.
c.Phương trình Bernulli cho ñưIng dòng
Xét cht lng lý tưng không nén ñư9c, chuyn ñng d8ng dư,i tác d.ng ca
lc có th là trCng lc. Khi ñó ta có phương trình Bernulli cho mt ñưHng dòng
như sau:
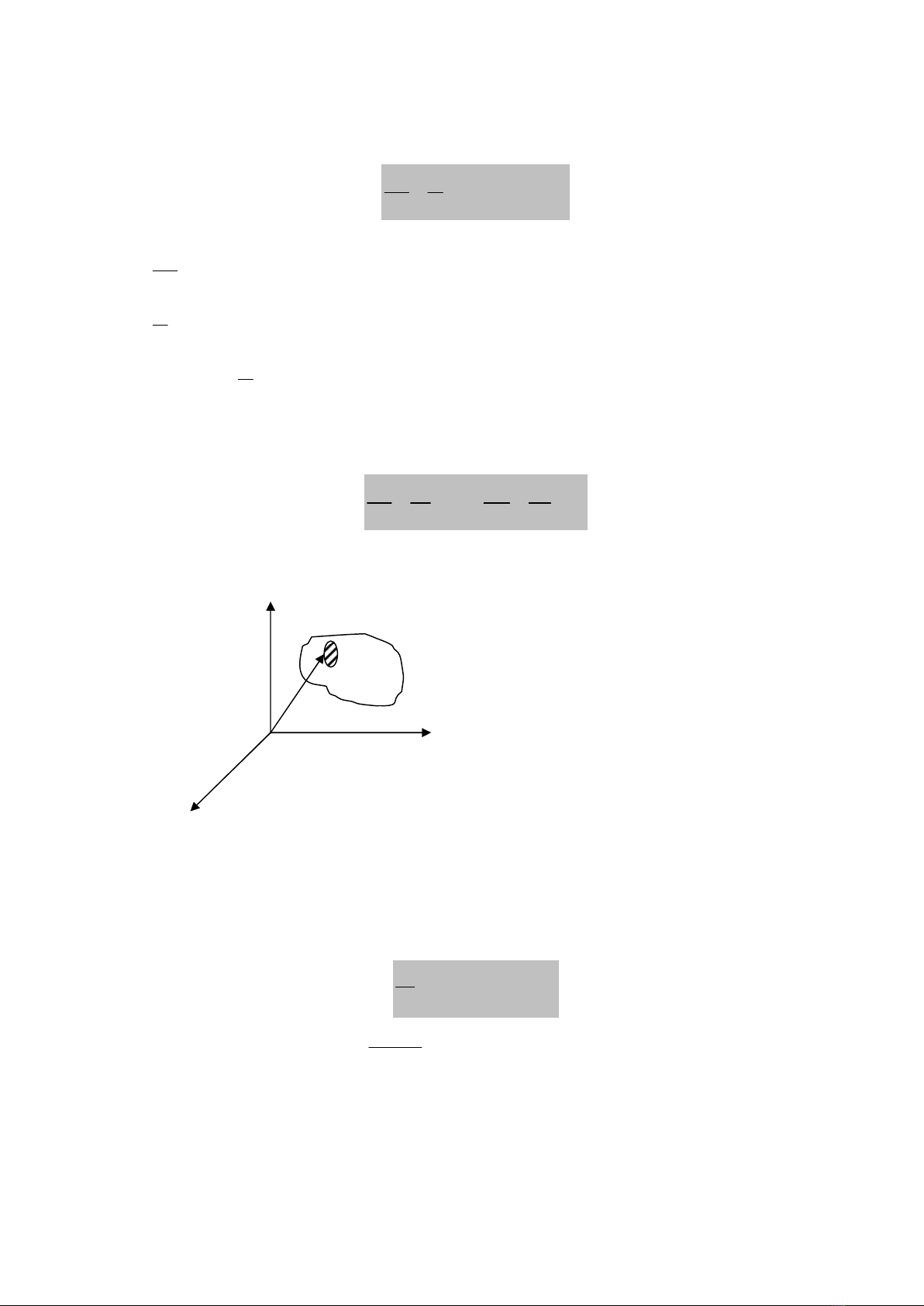
4
2
2
u p
z C const
g
γ
+ + = =
(4.13)
Ý nghĩa ca năng lư!ng Bernulli
2
2
u
g
– Te ñng năng: ñng năng ca 1 ñơn vP trCng lư9ng cht lng.
p
γ
– Te áp năng: kh' năng áp sut có th ñưa mt ñơn vP trCng lư9ng cht lưu
lên ñ cao
p
γ
so v,i mRt phgng xy.
z – Te vP năng.
T=ng ba ñ-i lư9ng gCi là te năng.
Xét hai ñim khác nhau trên 1 ñưHng dòng, ta có
2 2
1 1 2 2
1 2
2 2
u p u p
z z
g g
γ γ
+ + = + +
(4.14)
ðây chính là ñPnh luQt b'o toàn năng lư9ng ca cht lng lý tưng
5.ðMNH LÝ ðNG LƯNNG – ðMNH LÝ MOMEN ðNG LƯNNG
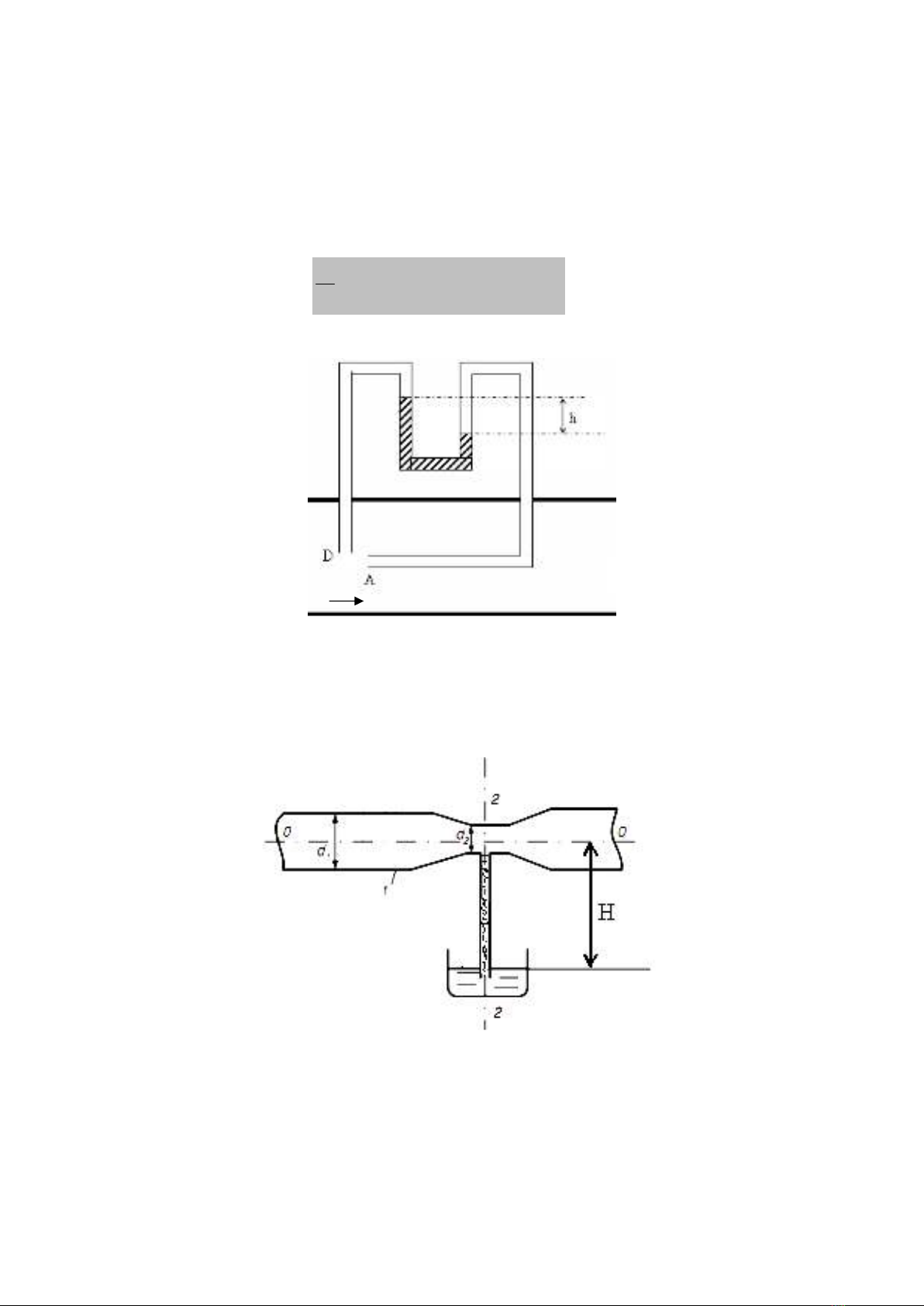
Xét mt th tích hhu h-n V ñư9c
bao quanh bi mRt kín S trong cht
lng ñang chuyn ñng.
MRt kín S bao quanh th tích hhu
h-n gCi là mRt kim soát. Th tích V
gCi là th tích kim soát.
a.ðOnh lý ñAng lưQng ñRi v=i th? tích chSt lTng hUu hVn
ðng lư9ng ca kh)i cht lng chuyn ñng:
V
K udV
ρ
=
∫∫∫
ðnh lý
1
n
e
k
k
V
d
udV F
dt
ρ
=
=
∑
∫∫∫
(4.15)
⇒
(
)
1
n
e
n k
k
V S
u
dV uu dS F
t
ρρ
=
∂+ =
∂
∑
∫∫∫ ∫∫
n
u
là hình chiu ca
u
lên phương pháp tuyn ngoài ca mRt
S
t-i ñim kh'o
sát.
d
x
z
y
0
r
S
5
b. ðOnh lý mômen ñAng lưQng ñRi v=i th? tích chSt lTng hUu hVn
Mômen ñng lư9ng ñ)i v,i tâm 0:
(
)
0
V
L r u dV
ρ
= ∧
∫∫∫
ðnh lý
( )
( )
0
1
n
e
k
k
V
d
r u dV m F
dt
ρ
=
∧ =
∑
∫∫∫
(4.16)
6. VÍ D[
Ví d\ 1.
ð ño vQn t)c ca dòng nư,c, ngưHi ta ñRt vào mt )ng pito AD hình chh
U
có
cha thy ngân (hình vm) sao cho ñOu A hư,ng vN dòng t,i ca dòng ch'y và
ñOu B hư,ng vuông góc v,i dòng t,i. NgưHi ta ño ñ chênh ct thy ngân
trong )ng là
h
.
Ví d\ 2.
B qua t=n tht năng lư9ng, xác ñPnh ñưHng kính d
2
ca mRt cSt co hnp ca
)ng ñ khi cho mt lưu lư9ng nư,c qua )ng là
8.8 /
Q l s
thì nư,c trong )ng
ñRt t-i mRt cSt co hnp sm ñư9c hút lên mt ñ cao
H=55cm
. ðưHng kính )ng t-i