
CHÖÔN G III: ÑOÄN G HOÏC CHÂT
L UƯ
I. Hai phöông phaùp moâ taû chuyeån
ñoäng cuûa löu chaát.
II. M t s khái ni m th ng dùngộ ố ệ ườ
III. Ph ng trình Bernoulli ươ
IV. Phaân loïai chuyeån ñoäng
V. Gia toác toaøn phaàn cuûa phaàn
töû löu chaát
VI. Phaân tích chuyeån ñoäng cuûa löu
chaát
VII. Ph ng pháp th tích ki m soát và đo hàm ươ ể ể ạ
c a m t tích phân kh iủ ộ ố
VIII. ng d ng ph ng pháp th tích ki m soátỨ ụ ươ ể ể
IX. Bài t p áp d ng.ậ ụ

1). Ph ng pháp Lagrange: ươ la ph ng pha p ươ
thông dung trong c hoc vât răn nghi a la khao / ơ / / 0
sa t s chuyên đông cua ca c ư/ 0 / 0 phân t chât l u ư0 ư
so v i ơhê truc chon tr c/ / / ươ . Luât /chuy n đng ể ộ
chuy n đng ể ộ
c aủ
c aủ phân t chât l u ư0 ư
phân t chât l u ư0 ư đc xa c đinh b i ca c ươ/ / ơ0
đc xa c đinh b i ca c ươ/ / ơ0
ph ng tri nh:ươ
ph ng tri nh:ươ
Chuy n đng cua chât l u co thê mô ta băng ể ộ 0 ư 0 0
hai ph ng pha p: ươ ph ng pháp Lagrange ươ va
ph ng pha p Euler ươ
0
f( r = t r ),
rr
2
2
dr du d r
u = a = =
dt dt dt
� �
r r
r
r
r
I. Hai phöông phaùp moâ taû chuyeån ñoäng cuûa löu
chaát
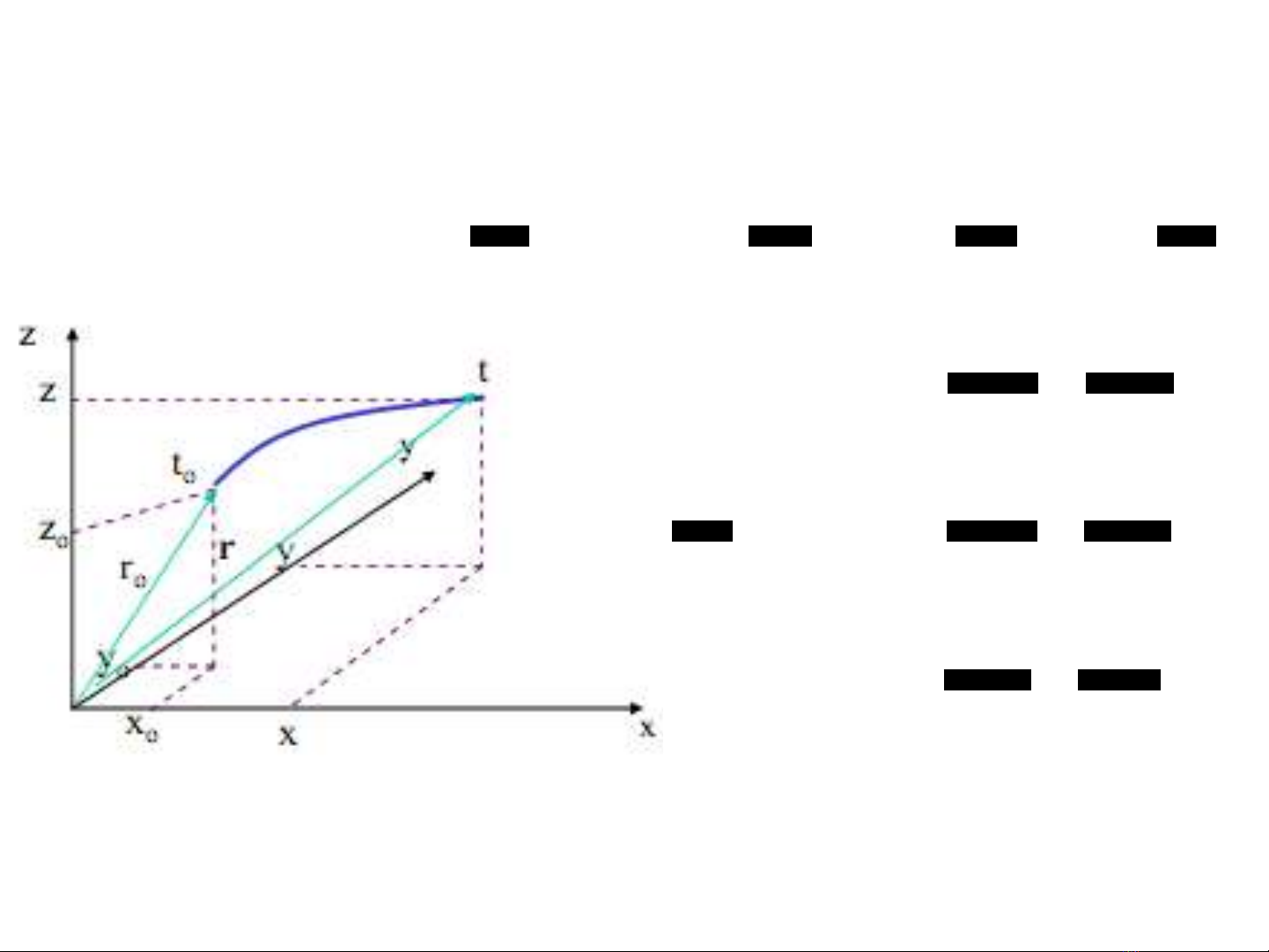
1). Ph ng pháp Lagrangeươ
Trong phöông phaùp Lagrage , caùc yeáu
toá chuyeån ñoäng chæ phuï thuoäc vaøo
thôøi gian, VD: u = at2 +b
0
f(r r = ),t
rr
x y z
dr dx dy dz
u = u = ; u = ; u =
dt dt dt dt
r
r
2
x
x2
2
y
y2
2
z
z2
du d x
a = =
dt dt
du
du d y
a = a = =
dt dt dt
du d z
a = =
dt dt
r
r
I. Hai phöông phaùp moâ taû chuyeån ñoäng cuûa löu
chaát (tt)

1). Phöông phaùp Lagrange:
Dươ>i da/ng tươ@ng minh chuyeån ñoäng cuûa theå
tích löu chaát ñöôïc moâ taû bôûi vò trí cuûa caùc
phaàn töû theo thôøi gian cuûa theå tích:
Öu ñieåm: moâ taû chuyeån ñoäng moät caùch chi
tieát.
Khuyeát ñieåm: soá löôïng phöông trình phaûi
giaûi quaù lôùn (3n); khoâng theå moâ taû cuøng
moät luùc quyõ ñaïo cuûa nhieàu phaàn töû.
Khaû naêng aùp duïng: phoøng thí nghieäm.
( )
( )
( )
2
x
0 0 0 x2
x
2
y
0 0 0 y y 2
2
z
zz2
0 0 0
du d x
dx
x=x x ,y ,z ,t a = =
u = dt dt
dt
du
dy d y
y=y x ,y ,z ,t u = a = =
dt dt dt
dz du d z
u = a = =
z=z x ,y ,z ,t dt dt dt
� �
� �
� � �
� � �
� � �
� � �
I. Hai phöông phaùp moâ taû chuyeån ñoäng cuûa löu
chaát (tt)

2). Phöông phaùp Euler:
Trong tr ng h p tông qua t ươ ơ , ng i ta th ng nghiên ươ ươ
c u ưchuyên đông cua chât l u băng ph ng pha p 0 ư ươ le.Ơ
Chuyeån ñoäng cuûa theå tích löu chaát ñöôïc
quan nieäm laø tröôøng vaän toác vaø ñöôïc moâ
taû bôûi moät haøm vaän toác lieân tuïc theo
khoâng gian vaø thôøi gian:
Öu ñie åm: chæ coù 3 phöông trình.
Kh u y e át ñie åm: khoâng cho thaáy roõ caáu truùc
cuûa chuyeån ñoäng.
Kh a û n a ên g a ùp d u ïn g : tính toaùn.
Gia tôc
Quy đao
( )
( )
( )
x x
y y
x y
u = u x,y,z,t
u = u ) u = u x,y,z,t
u = u x,y,
(r,
z
t
,t
� �
� �
� �
� �
� �
� �
�
r r r
I. Hai phöông phaùp moâ taû chuyeån ñoäng cuûa löu
chaát (tt)














![Bài tập trắc nghiệm Kỹ thuật nhiệt [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250613/laphong0906/135x160/72191768292573.jpg)
![Bài tập Kỹ thuật nhiệt [Tổng hợp]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250613/laphong0906/135x160/64951768292574.jpg)

![Bài giảng Năng lượng mới và tái tạo cơ sở [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2024/20240108/elysale10/135x160/16861767857074.jpg)








