4/18/2022
1
CBGD: ThS. TRÀ NGUYỄN QUỲNH NGA
BỘ MÔN CƠ LƯU CHẤT
tnqnga@hcmut.edu.vn
TRƯỜNG ĐẠI HỌC BÁCH KHOA TPHCM
Tháng 04 năm 2022
2
CHƯƠNG 5: DÒNG CHẢY ĐỀU TRONG ỐNG
1. Dòng chảy trên bản phẳng
2. Dòng chảy trong đường ống
3. Phương trình cơ bản của dòng chảy trong ống
4. Phân bố vận tốc trong dòng chảy tầng phát triển hoàn toàn trong ống
5. Phân bố vận tốc trong dòng chảy rối
6. Tính toán mất năng
7. Các dạng bài toán đường ống
4/18/2022
2
Một sốví dụvềđường ống trong kỹthuật
Hệ thống ống trong PCCC
Hệ thống ống dẫn khí (Nhà máy khí-điện-đạm Cà Mau)
Chương 5: DÒNG CHẢY ĐỀU TRONG ỐNG tnqnga@hcmut.edu.vn
3
taàng
Ñoaïn daàu chaûy taàng
Re = VL/< Rephaân giôùi
ÖÙùng vôùi lôùp bieân chaûy taàng
L=0 L=Ltôùi haïn Ñoaïn chaûy roái
Re = VL/> Rephaân giôùi
ÖÙùng vôùi lôùp bieân chaûy roái
roái
Caùc maáu nhaùm
Lôùp bieân taàng ngaàm coù beà daøy
taàng ngaàm
taàng ngaàm >: rối thành trơn
taàng ngaàm<: rối thành nhám
I. DOØNG CHAÛY TREÂN BAÛN PHAÚNG
4
Bản phẳng
4/18/2022
3
II. DOØNG CHAÛY TRONG OÁNG
Ta hình dung doøng chaûy trong oáng gioáng nhö doøng chaûy qua baûn phaúng ñöôïc cuoän troøn
laïi. Nhö vaäy theo lyù thuyeát , ôû ñaàu vaøo cuûa oáng coù moät ñoaïn maø doøng chaûy ôû cheá ñoä
chaûy taàng, roài sau ñoù môùi chuyeån sang chaûy roái.
Ñoaïn ñaàu oáng chaûy taàng
L=0 L=Ltôùi haïn Ñoaïn tieáp theo chaûy roái
Vaãn toàn taïi lôùp bieân taàng ngaàm
coù beà daøy taàng ngaàm
Loõi roái
Vò trí lôùp bieân
taàng ñaõ phaùt
trieån hoaøn
toaøn
5
III. PHÖÔNG TRÌNH CÔ BAÛN CHO DOØNG ÑEÀU TRONG OÁNG
Trong oáng xeùt ñoaïn vi phaân doøng chaûy ñeàu hình truï coù dieän tích dA nhö hình veõ:
 
   0
Ta coù : J = hd/ L laø ñoä doác thuyû löïc, L laø chieàu daøi ñoaïn doøng chaûy
Töø pt cô baûn coù theå vieát :
0
max
0
max
r
r
ττhay
2
r
Jγτ



 ⇔

0FFFαsinG
ms21
F2=p2dA
F1=p1dA
Fms
G
Gsin
s
=max
=0
1
1
2
2
Maët chuaån
z1z2
L
Löïc taùc duïng treân phöông doøng chaûy
( phöông s) :
Phöông trình cô baûn cuûa doøng ñeàu
JRγτ
Suy ra:
ÖÙùng suaát tieáp tyû leä baäc nhaát theo r
2/Jrγτ
Hay:
6
4/18/2022
4
IV. PHAÂN BOÁ VAÄN TOÁC TRONG DOØNG CHAÛY TAÀNG PHAÙT TRIEÅN HOAØN TOAØN TRONG OÁNG
hay
2
o
2
max
r
r
1uu
Phaân boá vaän toác trong chaûy taàng coù daïng Parabol
dr
du
μτ
Newton
2
r
Jγτ
P.Tr.C.Baûn
2
r
Jγ
dr
du
μ
C
μ4
r
Jγu
2
ou
r
dr r
parabol
r
r0
dr
μ2
r
Jγu
22
o
rr
μ4
Jγ
u
Taïi tâm r=0 ta coù u=umax
2
omax
r
μ4
Jγ
u
Taïi thành r=r0ta coù u=0
μ4
r
JγC
2
0
2
o
22
o
max
r
rr
uu
dr
μ2
r
Jγdu
7
ro
r
dA
Löu löôïng vaø vaän toác trung bình trong doøng chaûy taàng trong oáng :
2
o
2
max
r
r
1uu
0 0
r r
2 2
max 0
2
0
0 0
2
0 max max
2 u
dQ udA u.2 rdr Q 2 urdr (r r )rdr
r
r u Q u
Q V
2 A 2
8
4/18/2022
5
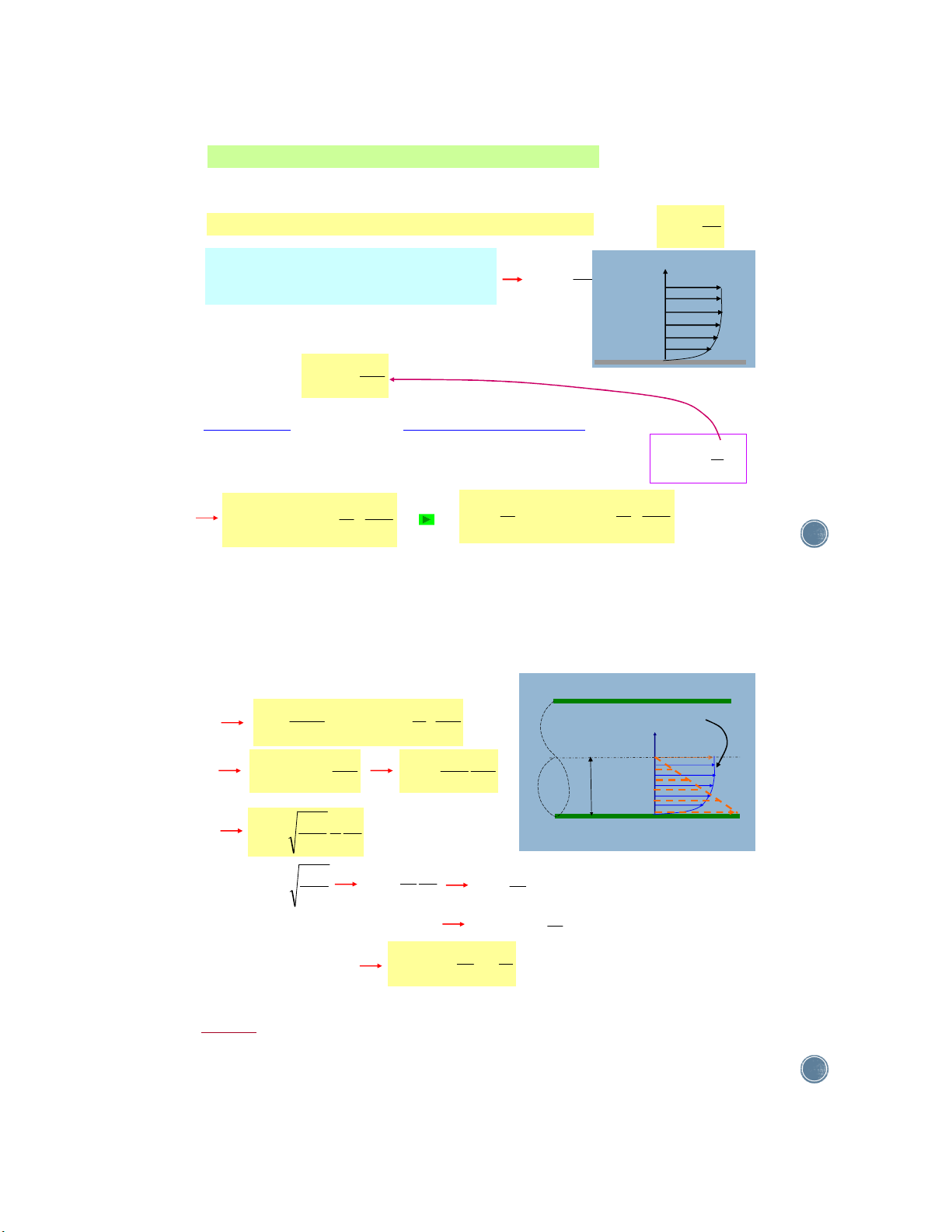
V.PHAÂN BOÁ VAÄN TOÁC TRONG DOØNG CHAÛY ROÁI
Ñoái vôùi doøng chaûy roái trong oáng, öùng suaát tieáp phuï thuoäc chuû yeáu vaøo ñoä chuyeån ñoäng hoãn
loaïn cuûa caùc phaân töû löu chaát, do ñoù:
=taàng +roái ;vì roái >> taàng neân ta boû qua taàng
Theo Prandtl: öùng suaát nhôùt roái khoâng phuï thuoäc vaøo tính nhôùt cuûa löu chaát.
Nhaän xeùt:
Töø thí nghieäm , Nikudrase cho raèng chieàu daøi xaùo troän l trong oáng:
2/1
o
r
y
1kyl
k : haèng soá Karman ( k = 0,4)
roi
du
dy
Neáu ñaët:
Theo giaû thieát cuûa Prandtl, phuï thuoäc vaøo
chieàu daøi xaùo troän vaø gradient vaän toác, goïi laø
öùng suaát nhôùt roái, vaø tính baèng:
dy
du
lρε
2
yu
y : khoaûng caùch töø thaønh ñeán lôùp chaát loûng ñang xeùt
l :chieàu daøi xaùo troän
Nhö vaäy:
2
2
roi
2
l
dy
2
2 2
roi
2
0
y du
k y 1
r dy
2
2 2
max
2
0 0
r y du
k y 1
r r dy
9
Nhö vaäy: Phaân boá löu toác trong tröôøng hôïp chaûy roái coù daïng ñöôøng logarit
Nhaän xeùt:söï phaân boá vaân toác trong tröôøng hôïp chaûy roái töông ñoái ñoàng ñeàu , gaàn vôùi vaän toác
trung bình hôn so vôùi tröôøng hôïp chaûy taàng. Ñoù cuõng laø lyù do taïi sao caùc heä soá hieäu chænh
ñoäng naêng ()hay heä soá hieäu chænh ñoäng löôïng () coù theå laáy baèng 1
y
u
ro
omax
Umax
Đường cong logarit
Neáu ñaët goác toaï ñoä taïi thaønh oáng:
2
2
0
22
0
0
max
dy
du
r
y
1ykρ
r
yr
τ
2
2
22
max
dy
du
ykρτ
2
2
2
max
2
y
dy
kρ
τ
du
y
dy
k
1
ρ
τ
du
max
Ñaët
max
*
u
(u*: vaän toác ma saùt)
y
dy
k
u
du
*
CyLn
k
u
u
*
Taïi taâm oáng r = ro, u = umax
o
*
max
rLn
k
u
uC
y
r
Ln
k
u
uu
o
*
max
10