110/31/2014
Chương 4
4.1_ Khái niệm tính ổn định
4.2_ Tiêu chuẩn ổn định đại số
(Routh, Hurwitz)
4.3_ Tiêu chuẩn ổn định tần số
(Nyquist, Bode)
4.4_ Phương pháp quỹ đạo nghiệm
Khảo sát tính ổn định
của hệ thống
210/31/2014
4.1 Khái niệm tính ổn định
Ổn định là yêu cầu cơ bản của hệ thống ĐKTĐ.
Ổn định BIBO: (Bound Input- Bound Output, vào chặn ra chặn)
Hệ thống được gọi là ổn định BIBO nếu với tín hiệu vào hữu hạn
thì tín hiệu ra cũng hữu hạn. Tức là nếu |r(t)|<thì |y(t)|< .
Ví dụ: hệ ổn định BIBO với r(t) = 1(t) thì y() = const.
Hệ thống
r(t) y(t)
Hệ ổn định không ổn định giới hạn ổn định
310/31/2014
4.1 Khái niệm tính ổn định
Ổn định tiệm cận (Lyapunov): Hệ ổn định tiệm cận nếu
như khi có nhiễu tức thời đánh bật hệ ra khỏi trạng thái
cân bằng thì sau đó hệ có khả năng tự quay về trạng thái
cân bằng ban đầu.
Hệ ổn định giới hạn ổn định
không ổn định
Với hệ tuyến tính thì hai khái niệm ổn định nêu trên là
tương đương. Hệ tuyến tính đạt ổn định BIBO thì cũng
sẽ ổn định tiệm cận và ngược lại.
410/31/2014
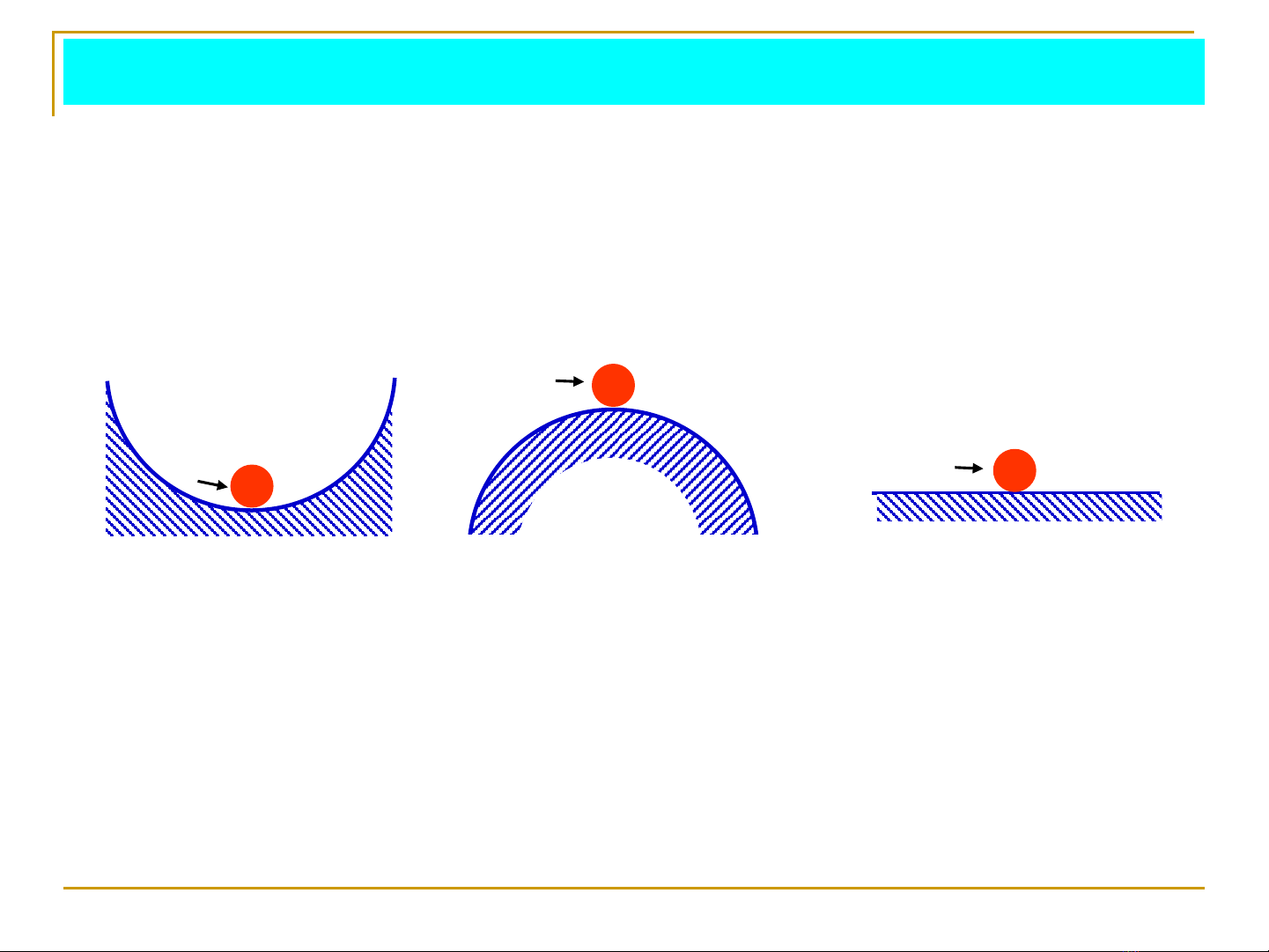
4.1 Khái niệm tính ổn định
Xét hệ thống tuyến tính có PTVP:
y0(t)_ là nghiệm riêng của PTVP.
yqđ(t)_ Là nghiệm tổng quát của PTVP khi vế phải bằng 0.
y(t) = y0(t) + yqđ (t)
11
1 0 1 0
11
nn
nn
nn
mm
mm
mm
d y d y d r d r
a a ... a y(t) b b ... b r(t)
dt dt dt dt
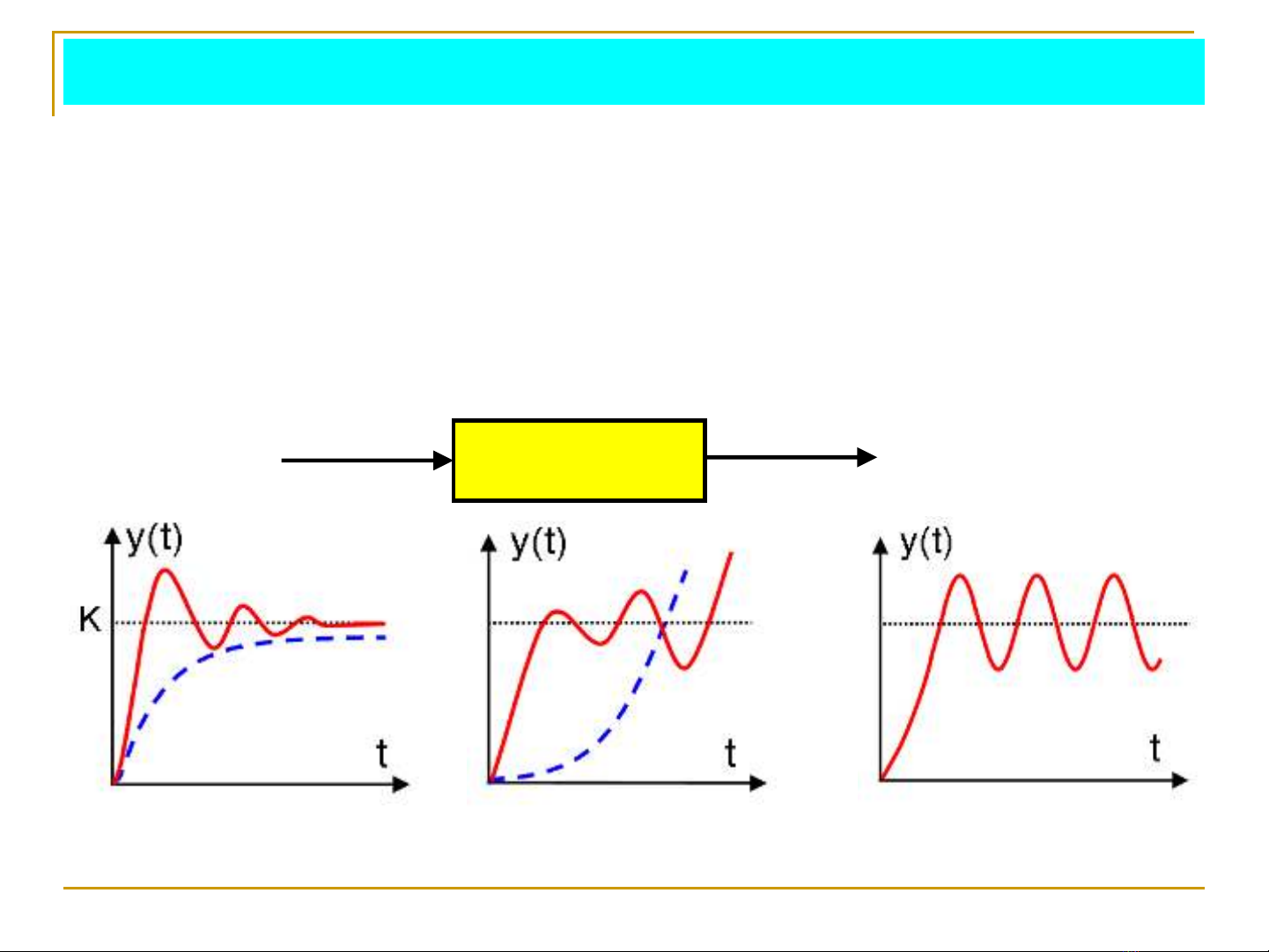
Đáp ứng của hệ cũng là nghiệm PTVP:
Ta thấy nếu r(t) hữu hạn thì y0(t) cũng hữu hạn, nên:
Tính ổn định của hệ chỉ phụ thuộc thành phần quá độ yqđ(t).
VD1, xét hệ có ptvp:
5 ( ) ( ) 2 ( )y t y t r t
Với r=1(t) thì y(t)= 2-2e-t/5 trong đó y0(t)=2 ; yqđ(t)=-2e-t/5
VD2, xét hệ có ptvp:
( ) 2 ( ) 5 ( ) 5 ( ) 5 ( )y t y t y t r t r t
y(t)= 1-e-tcos2t+2e-tsin2t = 1-(1/2+j)e(-1+2j)t - (1/2-j)e(-1-2j)t
510/31/2014
4.1 Khái niệm tính ổn định
Từ nhận xét nêu trên ta có thể định nghĩa cách khác về ổn định:
Một hệ thống tuyến tính được gọi là ổn định nếu quá trình quá
độ tắt dần theo thời gian. Hệ thống không ổn định nếu QTQĐ tăng
dần. Hệ thống ở giới hạn ổn định nếu QTQĐ không đổi hoặc dao
động với biên độ không đổi .
Tổng quát:
Ci_là hằng số phụ thuộc thông số của hệ và điều kiện đầu.
si_là nghiệm của phương trình đặc tính:
sicũng gọi là cực của hệ thống.
sicó thể là số thực (=i) hay số phức (=i ji)
1
10
... 0
nn
nn
a s a s a
Hệ ổn định
1
0
i
nst
i
tt
i
lim (t) lim C e
qñ
y
1
() i
nst
i
i
y t C e
qñ
