2/14/2020
73
145
CHƯƠNG 3 Ổn định hệ thống
146
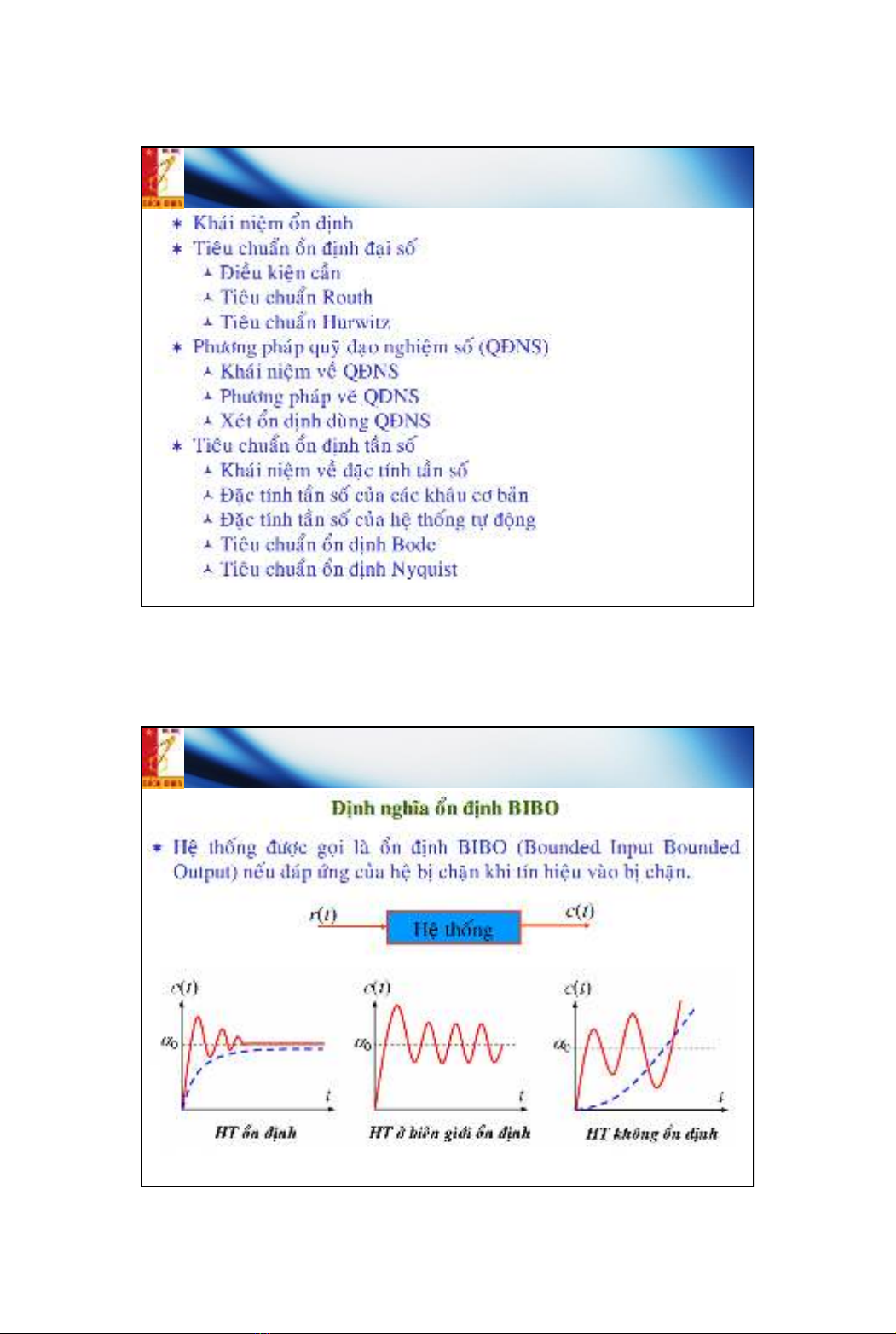
Định nghĩa ổn định
2/14/2020
74
147
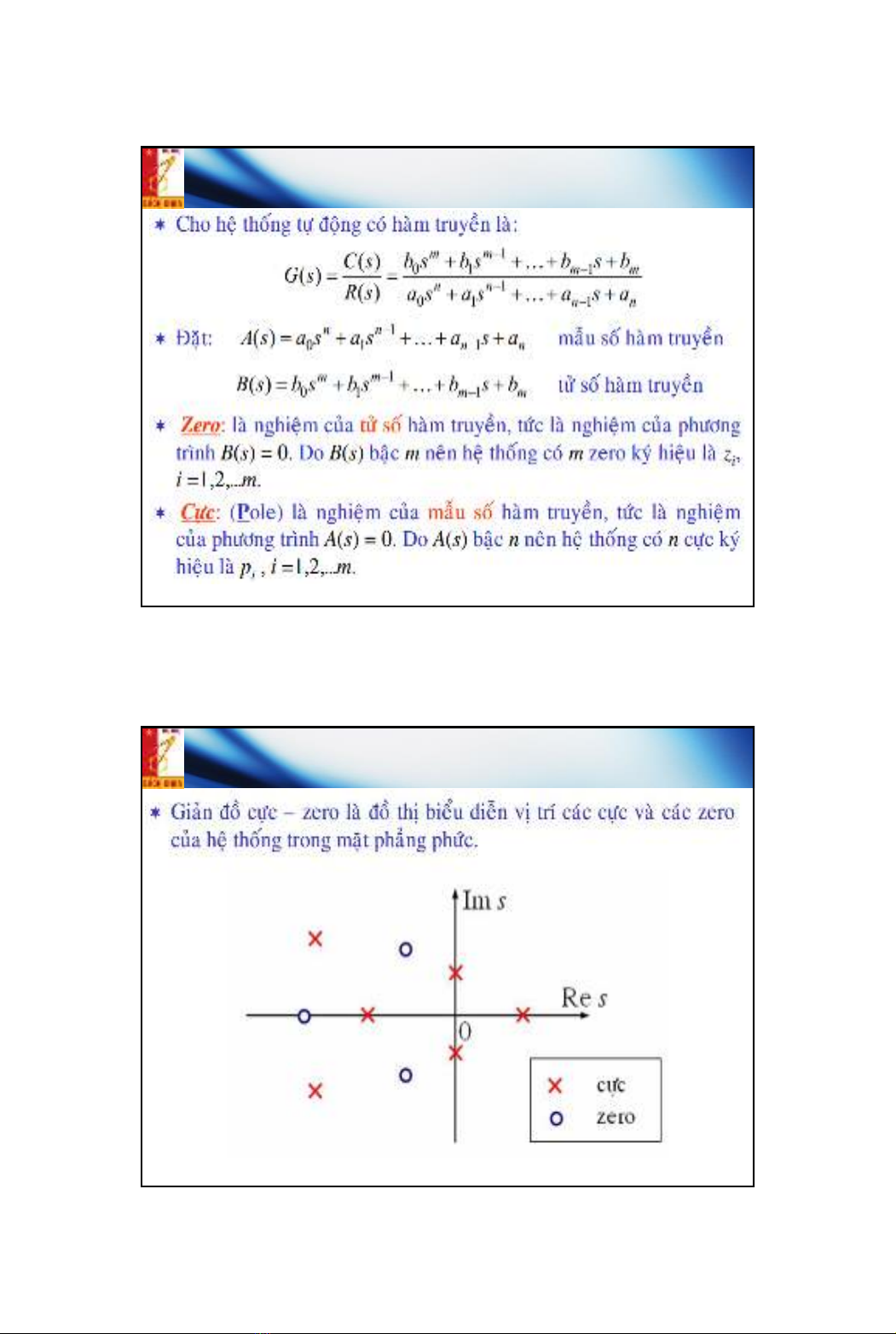
Điểm Cực và Zero
148
Giản đồ cực và zero
2/14/2020
75
149
Khái niệm ổn định
Điều kiện ổn định
Tính ổn định của hệ thống phụ thuộc vào vị trí các cực.
Hệ thống có tất cả các cực có phần thực âm (có tất cả các cực đều
nằm bên trái mặt phẳng phức): hệ thống ổn định.
Hệ thống có cực có phần thực bằng 0 (nằm trên trục ảo), các cực
còn lại có phần thực bằng âm: hệ thống ở biên giới ổn định.
Hệ thống có ít nhất một cực có phần thực dương (có ít nhất một
cực nằm bên phải mặt phẳng phức): hệ thống không ổn định.
150
Khái niệm ổn định
2/14/2020
76
151
Khái niệm ổn định
152
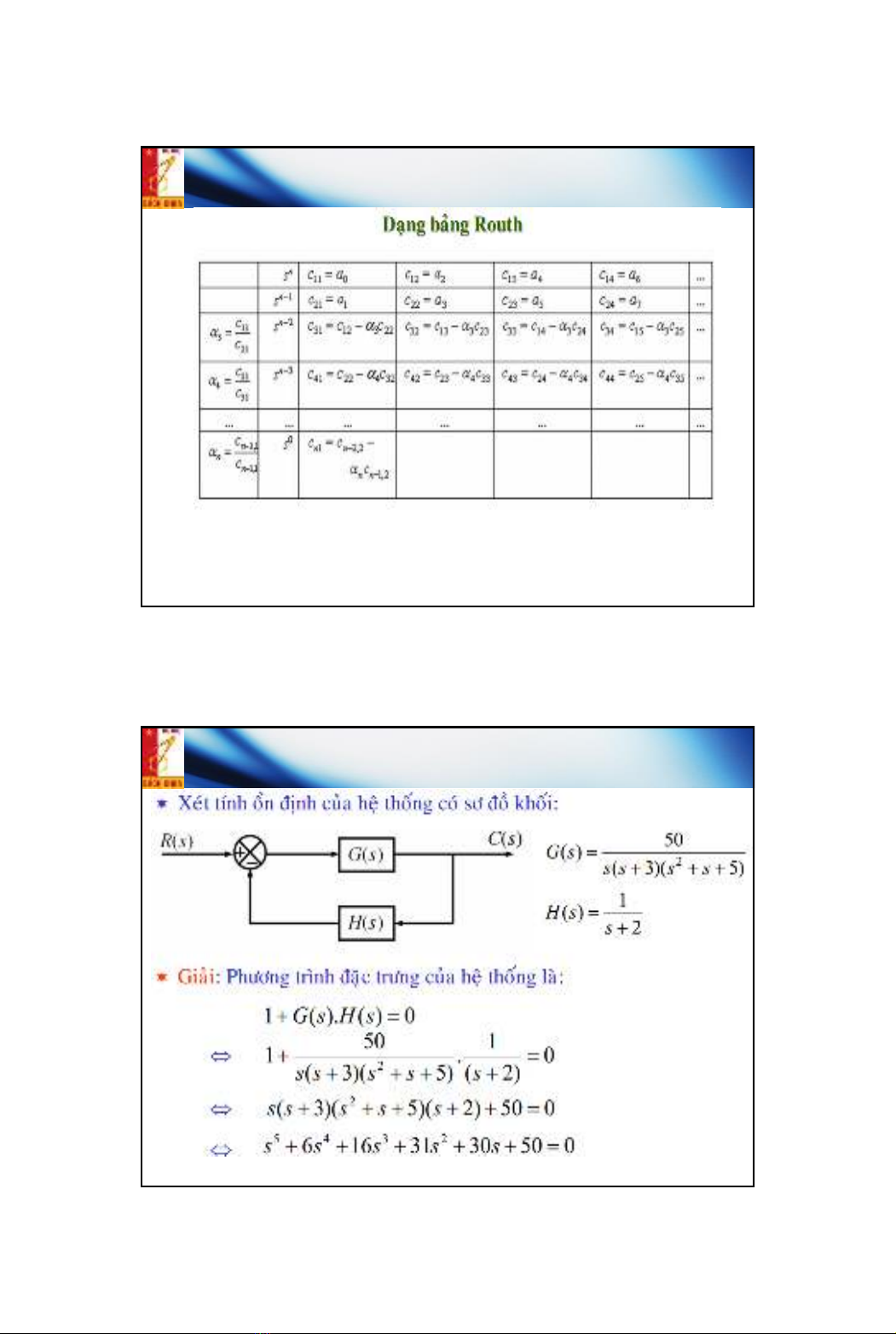
Tiêu chuẩn ổn định đại số Routh
2/14/2020
77
153
Tiêu chuẩn ổn định đại số Routh
Tiêu chuẩn ổn định đại số Routh:
Điều kiện cần và đủ để hệ ổn định là tất cả các phần tử ở cột 1 bảng Routh đều
cùng dấu, nếu có sự đổi dấu thì số lần đổi dấu bằng số nghiệm ở bên phải mặt
phẳng phức.
154
Thí dụ 3.1