j
=
w
=
=
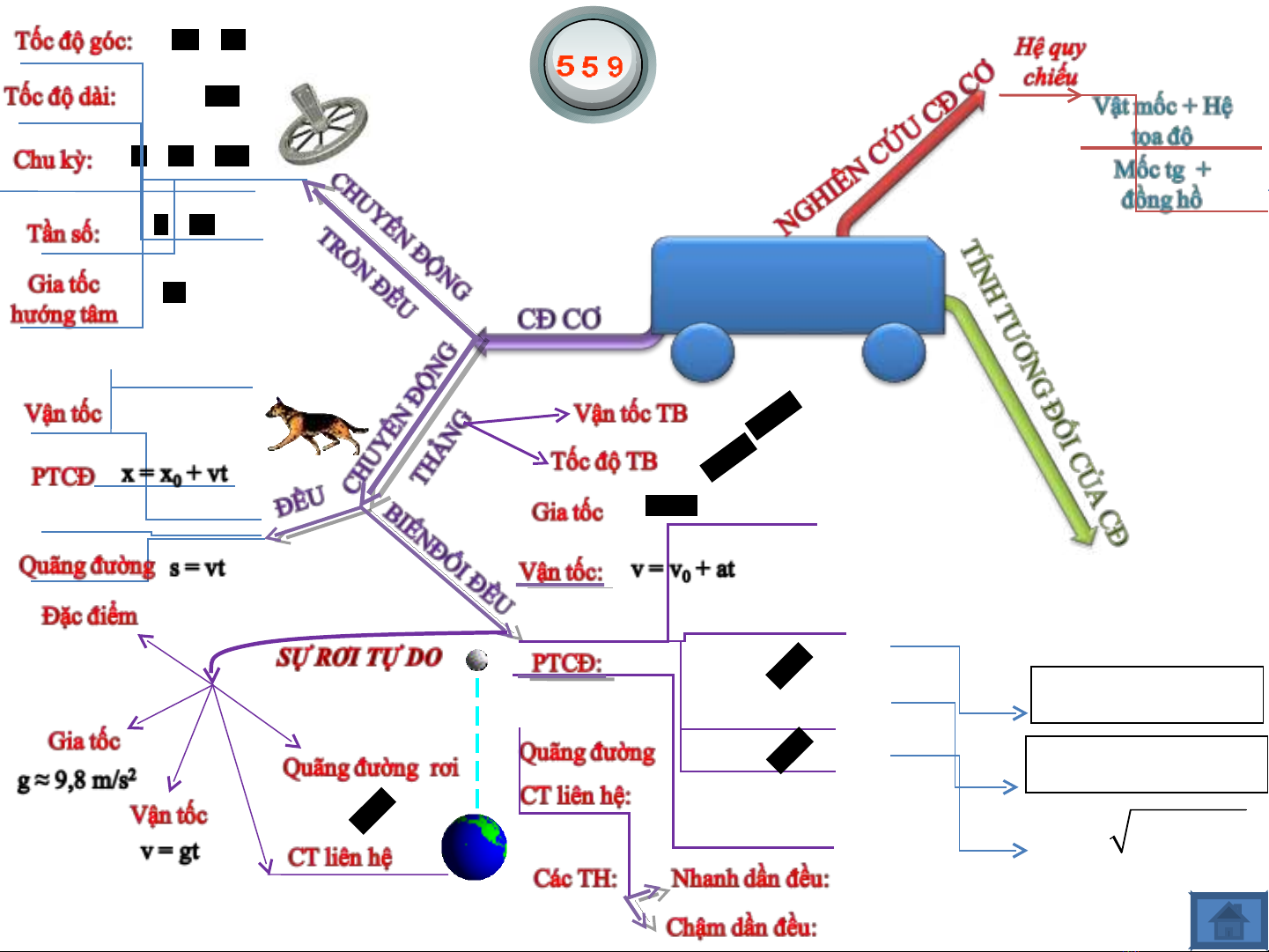
p 2 f
D
p 2 T r
w=
t =
v
=
=
=
T
r . p 2 w
1 f
p 2 T p 2 r v
w
=
=
f
p 2
2
D
Ộ
2
=
=
w
r
a ht
1 T v r
Ọ Ể
Ấ
Đ NG H C CH T ĐI M
ậ
ể
ộ
v = const
ỹ ạ Qu đ o và v n ố ủ ậ t c c a v t chuy n ụ ộ đ ng ph thu c vào HQC
D=
x
ườ
ẳ Đ ng th ng ? Ov
t
s
=
t
=
-
ồ ị ườ
ẳ
a
v v 0 t
Đ th : Đ ng th ng xiên góc
ồ ị ườ
ẳ
Đ th : đ
=
+
Công thức cộng vận tốc r v 1,2
r v 2,3
2
ng th ng xiên góc +
+
=
1
at
x
v t 0
x 0
2
v1,3 = v1,2 + v1,3
ồ ị ạ
Đ th : d ng parabol
CĐ th ng ẳ nhanh d n ầ đ uề
2
=
+
1
s
at
v t 0
(cid:0) (cid:0)
2
r v 1,2 r v 1,2
v1,3 = |v1,2 - v1,3|
2
(cid:0) (cid:0)
2
v
a x
2 .
=
1
s
gt
2
2
=
+
- D
v
as
2
v
= 2 v 0 = 2 v 0
r v 1,3 r v 2,3 r v 2,3 r v^r v 2,3 1,2
v 1,3
2 v 1,2
2 2,3
N u ế Δx ≡ s:
a.v > 0
2
=
v
gs
2
a.v < 0
-
i bài t p:
ươ ươ
ả ể ộ
Ph t ph
ọ
ị ộ ậ ầ ể ề ủ
0, v n t c đ u, gia t c.
ố ạ ượ ậ ố ầ ng x → tìm các đ i l
ế t ptcđ
ậ ặ
ế t ptcđ
ả ng trình
ậ ng pháp gi ế ng trình chuy n đ ng: 1. Bài toán vi ế ệ B1: Ch n h quy chi u B2: Xác đ nh v trí ban đ u c a v t, chi u chuy n đ ng c a ủ ị ậ v t B3: Vi 2. Bài toán 2 v t g p nhau: B1: Vi B2: i ph + Cách 1: Gi Khi 2 v t g p nhau: x
1 = x2 ọ ộ ặ
ả tìm t a đ g p → gi
ị Xác đ nh
ệ ụ ể ể ặ
ươ ừ ố trên xu ng ng t
ổ ề ư ậ ế ẳ ộ ươ ậ ặ → ể i pt đ tìm t → ẽ ồ ị ủ + Cách 2: V đ th c a 2 trên cùng h tr c (x,t) ậ ị ề ờ ế ể ừ giao đi m k t lu n v th i đi m và v trí g p giao đi m, t ơ ự ể ộ ậ do: 3. Bài toán v t chuy n đ ng r i t ố ọ ề ơ ể ộ ạ i đi m r i, chi u d Ch n g c t a đ t ả ậ ờ ướ i, g c th i gian lúc th v t. d → Gi ể ả ọ ố i bài toán nh v t chuy n đ ng th ng bi n đ i đ u.
ủ ậ ủ ậ ể ể ướ ướ ể ể i đây không th coi là i đây không th coi là
ộ ộ Bài 1: Chuy n đ ng c a v t nào d Chuy n đ ng c a v t nào d Bài 1: ơ ự ơ ự do: r i t do: r i t
ỏ ượ ỏ ượ ộ ộ ả ơ ừ ả ơ ừ ố ố A. M t viên đá nh đ A. M t viên đá nh đ c th r i t c th r i t ấ ấ trên cao xu ng đ t trên cao xu ng đ t
ư ư ỏ ỏ ạ ạ ắ ầ ơ ắ ầ ơ B. Các h t m a nh lúc b t đ u r i B. Các h t m a nh lúc b t đ u r i
ơ ừ ơ ừ ụ ụ ộ ộ ế ế ố ố ấ ấ C. M t chi c lá r ng đang r i t C. M t chi c lá r ng đang r i t trên cây xu ng đ t. trên cây xu ng đ t.
ủ ủ ơ ơ ố ố ẳ ẳ ặ ặ
ượ ượ ế ộ ế ộ D. M t chi c lông chim r i trong ng th y tinh đ t th ng D. M t chi c lông chim r i trong ng th y tinh đ t th ng ứ ứ đ ng và đã đ đ ng và đã đ c hút chân không. c hút chân không.
ọ Bài 2: Ch n câu tr l Bài 2:
ả ờ đúng i
ể
ế
ề
ẳ
ộ
ộ
ượ
ề
M t chi c thuy n chuy n đ ng th ng ng
c chi u
ướ ớ ậ ố
ố ớ
ướ
dòng n
c v i v n t c 7km/h đ i v i dòng n
c.
ớ ờ ậ ố ủ
ớ ậ ố
ướ
ả
N c ch y v i v n t c 2km/h so v i b . V n t c c a
ớ ờ
ề
thuy n so v i b là:
A. 9km/h
B. 8km/h
C. 5km/h D. 6km/h
ả ờ đúng i
ề
ố ộ
ng
ố ộ ằ
ủ
ể
ộ
ọ Bài 3: Ch n câu tr l Bài 3: ỗ ộ M t đĩa tròn có bán kính 36 cm, quay đ u m i vòng ố ướ trong 0,6s. Tính t c đ góc, t c đ dài, gia t c h tâm c a m t đi m n m trên vành đĩa
A. ω = 10,5 rad/s; v = 3,77 m/s; a = 39,48 m/s2
B.
ω = 1,05 rad/s; v = 3,77 m/s; a = 3948 m/s2
C. ω = 10,5 rad/s; v = 37,7 m/s; a = 39,48 m/s2
D. ω = 10,5 rad/s; v = 3,77 m/s; a = 394,8 m/s2
ộ
ượ
ộ
c mô t
ả ở ồ b i đ
ủ
ể
ể
ộ
ủ ể Bài 4: Chuy n đ ng c a m t xe máy đ Bài 4: ọ ị th sau. Ch n câu đúng: ộ Chuy n đ ng c a xe máy là chuy n đ ng:
ờ ề ừ
ầ
ậ 60
ờ ả
ề
60
ờ
ả
ừ ờ →
20 ờ
→ ả A. Đ u trong kho ng th i gian t 0 ờ ả ề 20s, ch m d n đ u trong kho ng th i 70s→ừ gian t ề ầ ậ B. Ch m d n đ u trong kho ng th i →ừ ầ gian t 20s, nhanh d n đ u trong 0 70s→ ừ ờ ả kho ng th i gian t ả ề ầ C. Nhanh d n đ u trong kho ng th i →ừ ờ ề 0 20s, đ u trong kho ng th i gian t 70s→ừ gian t 60 ả ề D. Đ u trong kho ng th i gian t ậ ả ề ầ 60s, ch m d n đ u trong kho ng th i →ừ 60 70s gian t
j
=
w
=
=
p 2 f
D
p 2 T r
w=
t =
v
=
=
=
T
r . p 2 w
1 f
p 2 T p 2 r v
w
=
=
f
p 2
2
D
Ộ
2
=
=
w
r
a ht
1 T v r
Ọ Ể
Ấ
Đ NG H C CH T ĐI M
ậ
ể
ộ
v = const
ỹ ạ Qu đ o và v n ố ủ ậ t c c a v t chuy n ụ ộ đ ng ph thu c vào HQC
D=
x
ườ
ẳ Đ ng th ng ? Ov
t
s
=
t
=
-
ồ ị ườ
ẳ
a
v v 0 t
Đ th : Đ ng th ng xiên góc
ồ ị ườ
ẳ
Đ th : đ
=
+
Công thức cộng vận tốc r v 1,2
r v 2,3
2
ng th ng xiên góc +
+
=
1
at
x
v t 0
x 0
2
v1,3 = v1,2 + v1,3
ồ ị ạ
Đ th : d ng parabol
CĐ th ng ẳ nhanh d n ầ đ uề
2
=
+
1
s
at
v t 0
(cid:0) (cid:0)
2
r v 1,2 r v 1,2
v1,3 = |v1,2 - v1,3|
2
(cid:0) (cid:0)
2
v
a x
2 .
=
1
s
gt
2
2
=
+
- D
v
as
2
v
= 2 v 0 = 2 v 0
r v 1,3 r v 2,3 r v 2,3 r v^r v 2,3 1,2
v 1,3
2 v 1,2
2 2,3
N u ế Δx ≡ s:
a.v > 0
2
=
v
gs
2
a.v < 0
-
