9/29/14
1
11
Chương II : MẠCH ĐIỆN XOAY CHIỀU HÌNH SIN
2.1 Khái niệm về mạch điện xoay chiều hình sin
2.2 Trị hiệu dụng của dòng điện xoay chiều hình sin
2.3 Biểu diễn các đại lượng xoay chiều hình sin
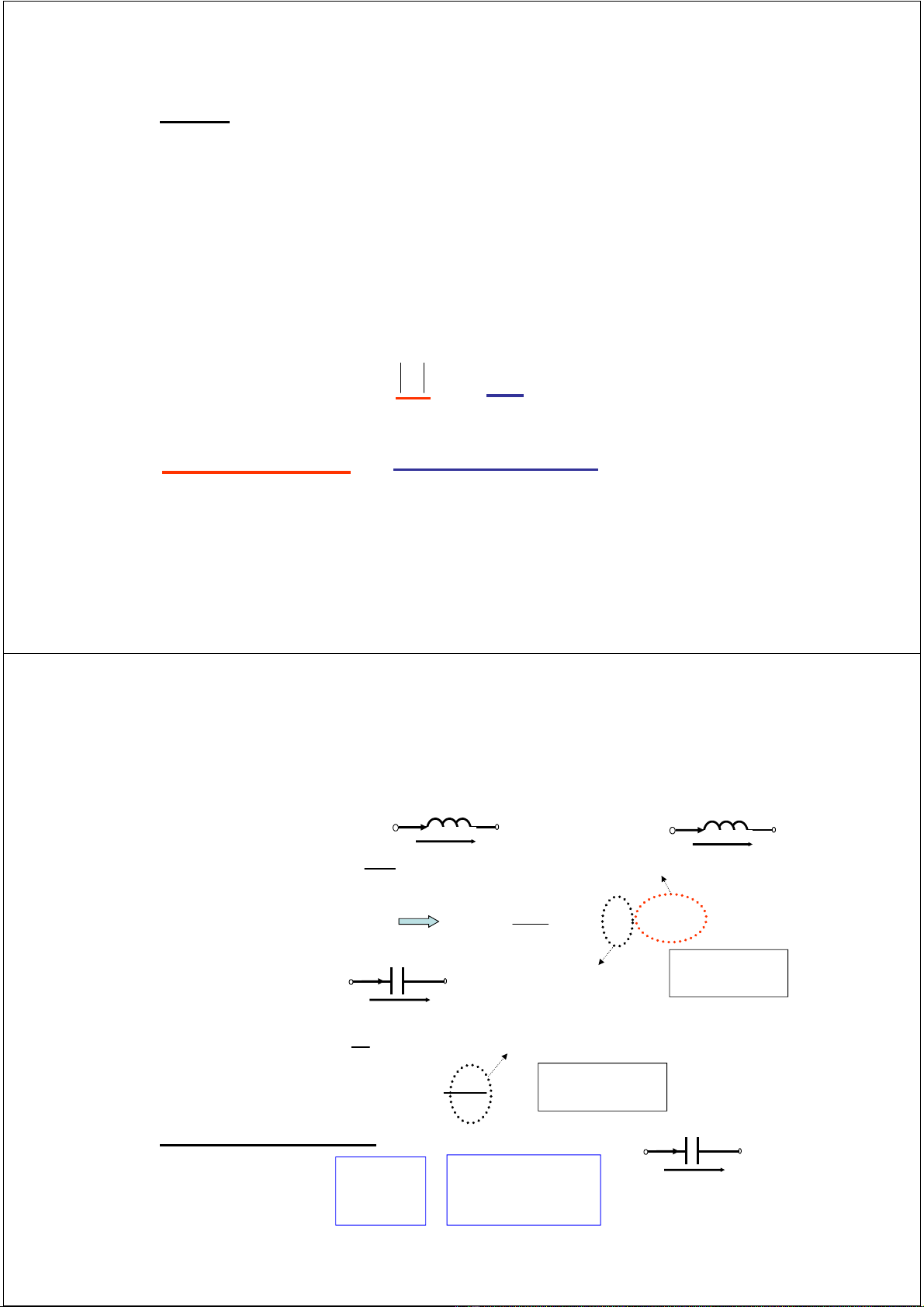
2.4 Phản ứng của nhánh với dòng điện xoay chiều hình sin
2.5 Công suất trong mạch điện xoay chiều 1 pha
2.6 Nâng cao hệsốcosϕ
ϕϕ
ϕ(bù công suất phản kháng)
9/29/14
2
2
0 1 2 3 4 5 6 7
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
t
i
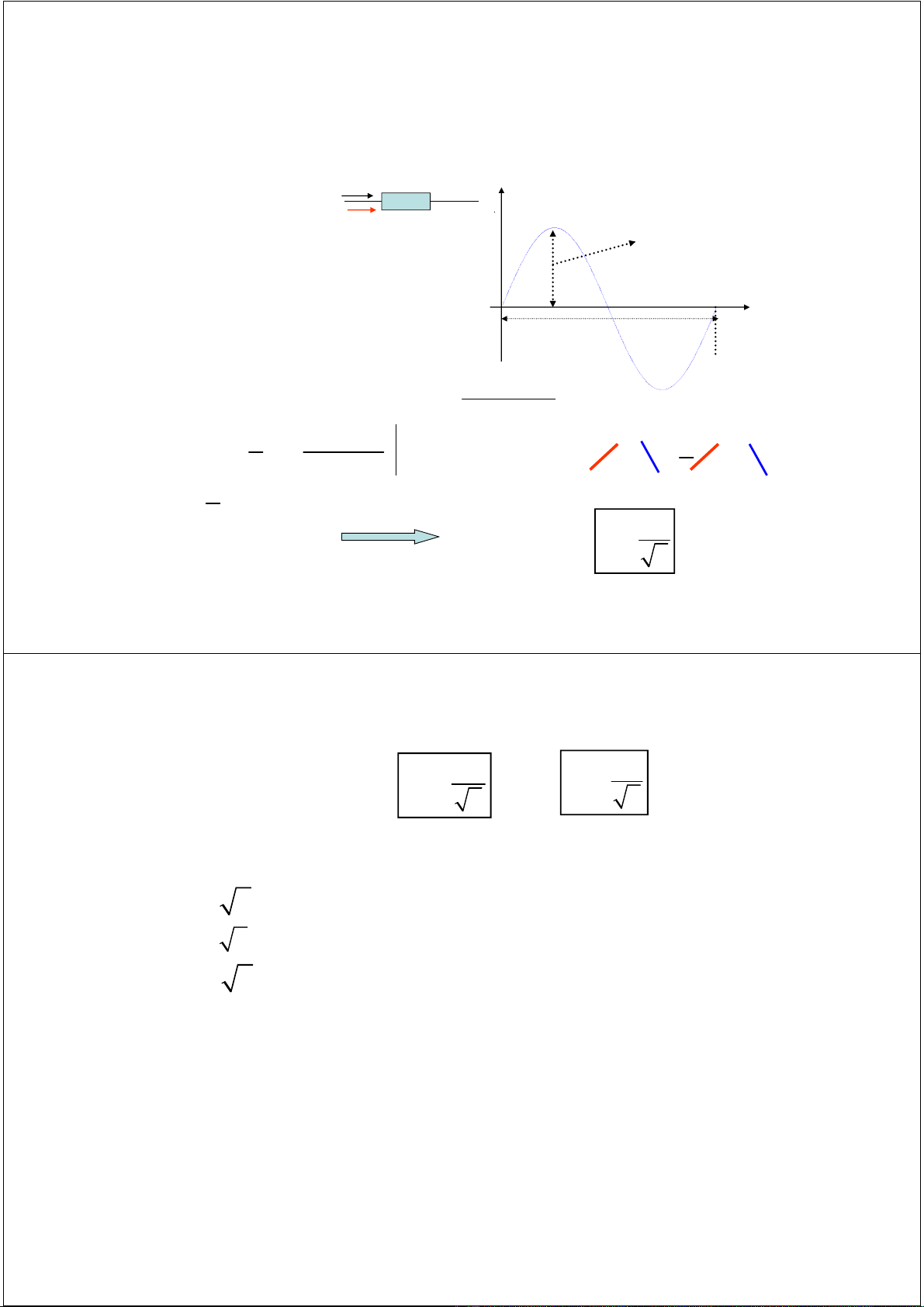
2.1 Khái niệm về mạch điện xoay chiều hình sin
m i
i I sin( t )
= ω + ψ
m u
u U sin( t )
= ω + ψ
m e
= ω + ψ
T
i
ψ
m
I
1
f
T
=
i
t
ω + ψ
2 f
ω = π
fcb = 50Hz T = 0,02s
Đặc trưng:
Biên độ
Tần số
Góc pha đầu
9/29/14
3
3
2 2
m
1
R I T R I T
2
=
i
0 1 2 3 4 5 6 7
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
T
m
I
t
2.2 Trị hiệu dụng của dòng điện xoay chiều hình sin
i
0
ψ =
A~ =
RIm2
a. Định nghĩa:
IR
Sau T: Ao= RI2T
Sau T:
T
2
0
Ri dt
∫
A~ =
m
i I sin t
= ω
i~
T
2
0
sin ( t)dt
ω
∫
A~=
= RIm2
T
0
1 cos(2 t)
dt
2
− ω
∫
RIm2
1 sin(2 t)
(t )
2 2
ω
−ω
Cân bằng 2NL
m
I
I
2
=
Trị hiệu dụng
0
T
2
~ m
1
A R I T
2
=
p = Ri2
Giá trịdòng một chiều tương đương vềnhiệt năng
9/29/14
4
4
Đặc trưng cho các đại lượng
xoay chiều hình sin cùng tần
số:
- Trịhiệu dụng ( I, U, E)
-Góc pha đầu ( ψi, ψu, ψe)
u
u 2U sin( t )
= ω + ψ
e
e 2E sin( t )
= ω + ψ
i
i 2I sin( t )
= ω + ψ
Khi so sánh các đại lượng xoay chiều hình sin cùng tần số:
ϕ
=
u i
ψ −ψ
- So sánh vềtrịhiệu dụng
- So sánh vềgóc pha
m
U
U
2
=
m
E
E
2
=
Tương tự :
Góc lệch pha giữađiện áp và dòng điện:
9/29/14
5
5
1. Véc tơ :
Đặc trưng cho 1 véc tơ:
A
và ϕ ϕ
A
Đặc trưng cho các đại lượng xoay chiều hình sin cùng tần số:
Trịhiệu dụng ( I, U, E) và góc pha đầu ( ψi, ψu, ψe)
Ký hiệu
* Ưu điểm: Trực quan
Định luật
Kiếc-khốp
* Lưu ý:
k n
k
k 1
I 0
=
=
=
∑
r
1 2
k n k n
k
k
k 1 k 1
U E
= =
= =
=
∑ ∑
ur ur
2.3 Biểu diễn các đại lượng xoay chiều hình sin
EUI
r
r
r
ox
ψu
ψi
ψe
E
r
I
r
U
r
A
r
x
0
9/29/14
6
30o
Giả sử có mạch điện
Biết :
0x
2
i
1
I
' arctg
I
ψ =
60o
Tìm : i = i1+ i2
i
i1i2
1
i 2 20sin( t 60 )
= ω +
2
i 210sin( t 30 )
= ω −
i
2 Isin( t )
= ω + ψ
2 2
1 2
I I I
= +
2 2
I 20 10
= +
= 22,36
ψi
ψi’
10
arctg
20
=
i
' 26 34'
ψ =
i
33 26'
ψ =
i 2.22,36sin( t 33 26 ')
= ω +
Kết quả:
21 III
r
r
r
+=
1
I
r
2
I
r
I
r
6
9/29/14
7
7
2. Số phức:
A = a + j b
A
ϕ
+1
+j
0
a, b : số thực
* Hai dạng biểu thi sốphức:
Dạng đại số: A = a + j b Dạng lũy thừa:
j
A A e
ϕ
=
* Quan hệ giữa 2 dạng:
a. Nhắc lại khái niệm vềsốphức
j: đơn vị ảo
- Biết dạng đại số: a + j b
A
=
2 2
a b
+
ϕ =
b
arctg
a
1
= −
1
j
=
- j
A
a
jb
•
j
A A e
ϕ
=
Biết dạng lũy thừa:
a =
b =
A cos
ϕ
A sin
ϕ
9/29/14
8
8
* Các phép tính + , - số phức
A1= a1+ j b1
= (a1±a2) + j (b1±b2) =
1
j
1
A e
ϕ
=
A2= a2+ j b2
2
j
2
A e
ϕ
=
* Các phép tính *, / số phức
(a1* a2-b1* b2) + j (a1b2+ a2b1) =
1
j
1
A e
ϕ
2
j
2
* A e
ϕ
1 2
j( )
1 2
A A e
ϕ +ϕ
=
j
A e
ϕ
=
1
2
A
AA
= =
j
A e
ϕ
=
a + j b
A = A1* A2= a + j b
1 2
1
j( )
2
Ae
A
ϕ −ϕ
hoặc
9/29/14
9
9
2. Chia 1 số cho j (nhân –j)
•Mô đun không đổi
•Góc cộng (-900)
b. Biểu thị các đại lượng xoay chiều hình sin bằng số phức :
Chú ý :
1. Nhân 1 số với j
•Mô đun không đổi
•Góc cộng 900
Đặc trưng cho số phức :
A
và ϕ
Đặc trưng cho đại lượng xoay chiều hình sin cùng tần số :
Trịhiệu dụng ( I, U, E) và góc pha đầu ( ψi, ψu, ψe)
Ký hiệu:
i
j
I Ie
•
ψ
=
u
j
U Ue
•
ψ
=
e
j
E Ee
•
ψ
=
9/29/14
10
10
C
C
1
U I
j C
• •
=ω
i
j
LL
I I e
•
ψ
=
i
j
L
LI e
ψ
* Các phép tính đạo hàm và tích phân số phức :
• Phép đạo hàm : iLL
uL
Dạng tức thời
L
L
di
u L
dt
=
Dạng phức:
L
LL
U jX I
• •
=
ILXL
UL
XL
(cảm kháng)
• Phép tích phân :
C
iC
uC
XC
IC
UC
Dạng tức thời:
C C
1
u i dt
C
=
∫
Dạng số phức:
C
CC
U jX I
• •
= −
XC(dung kháng)
I
•
j
ω
L
L
d I
U L
dt
•
•
= =
k n
k
k 1
I 0
=•
=
=
∑
1 2
k n k n
k
k
k 1 k 1
U E
= =
• •
= =
=
∑ ∑
Định luật Kiếc - khốp :