18/01/2015
1
1
0 1 2 3 4 5 6 7
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
t
i
Chư ơ ng II : MẠ CH ĐIỆ N XOAY CHIỀ U HÌNH SIN
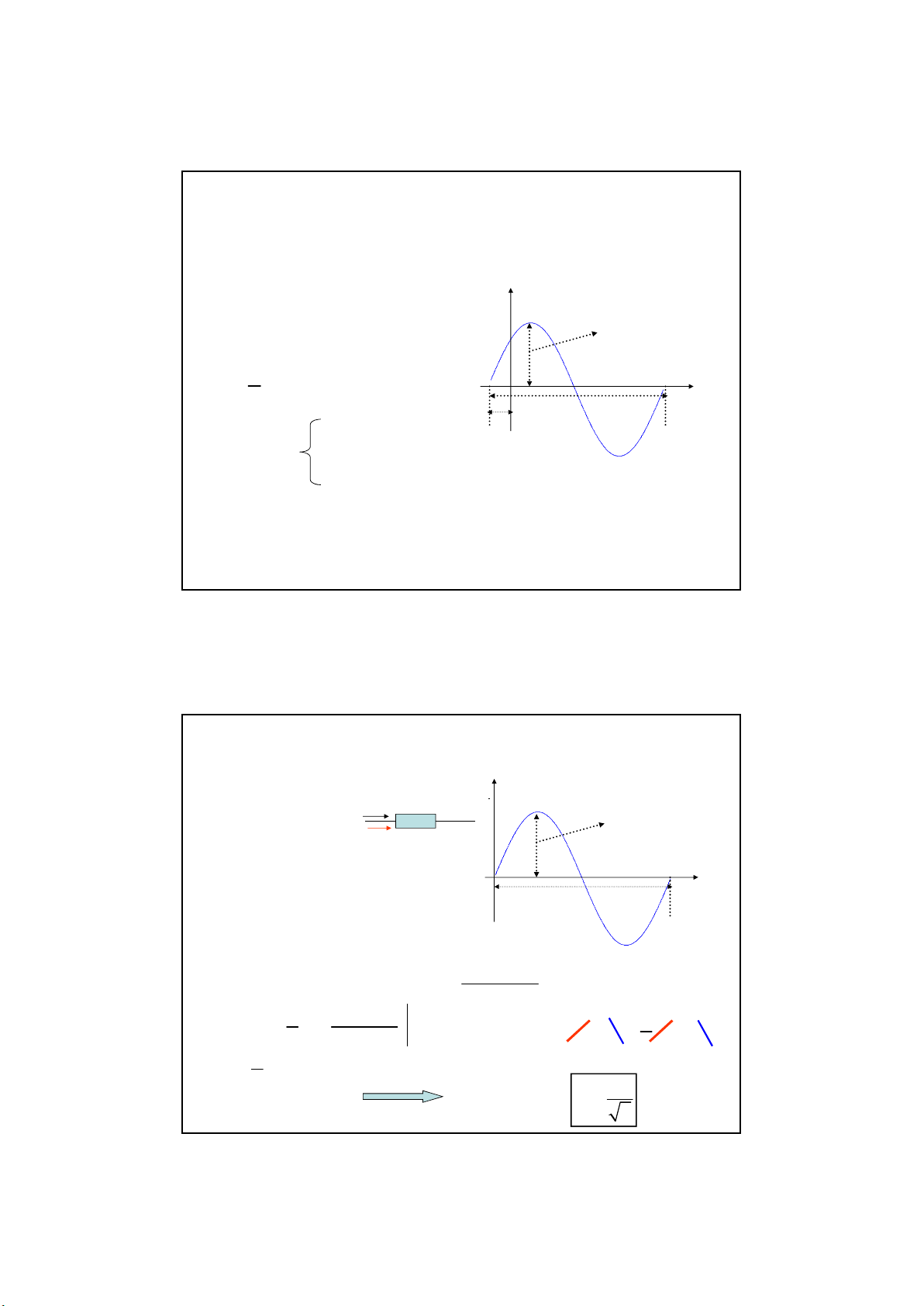
2.1 Khái niệ m về mạ ch điệ n xoay chiề u hình sin
m i
i I sin( t )
m u
u U sin( t )
m e
e E sin( t )
T
i
m
I
i
t
2 f
fcb = 50Hz T = 0,02s
Đặ c trư ng: Biên độ
Tầ n số
Góc pha đầ u
2
2 2
m
1
R I T R I T
2
i
0 1 2 3 4 5 6 7
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
T
m
I
t
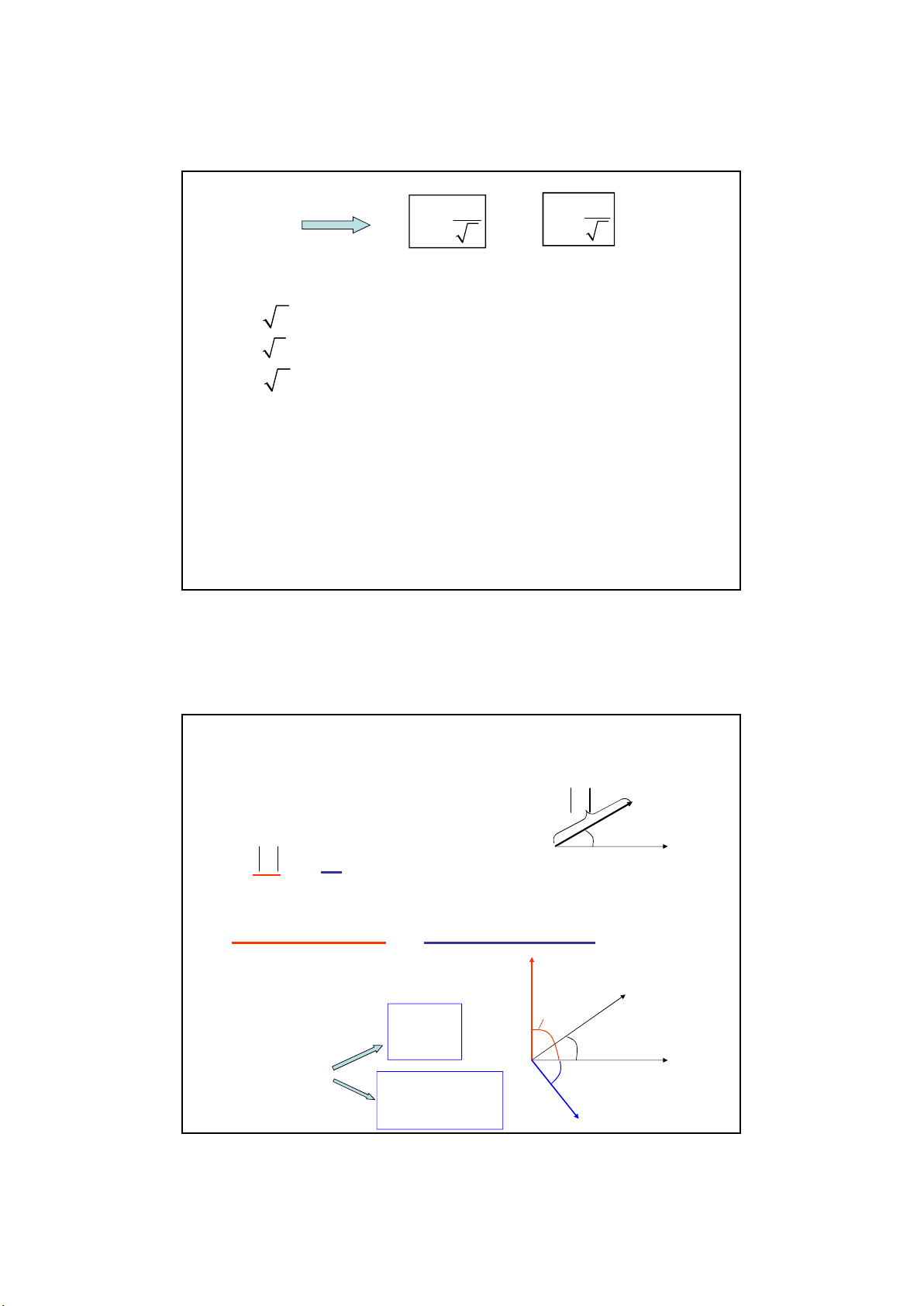
2.2 Trị hiệ u dụ ng củ a dòng điệ n xoay chiề u hình sin
i0
A~=
RIm2
a. Đị nh nghĩa: IR
Sau T: Ao= RI2T
Sau T:
T
2
0
Ri dt
A~=
m
i I sin t
i~
T
2
0
sin ( t)dt
A~=
= RIm2
T
0
1 cos(2 t)dt
2
RIm2
1 sin(2 t)
(t )
2 2
Cân bằ ng 2NL
m
I
I2
Trị hiệ u dụ ng
0
T
2
~ m
1
A R I T
2
p = Ri2
18/01/2015
2
3
Đặ c trư ng cho các đạ i lư ợ ng
xoay chiề u hình sin cùng tầ n
số :
-Trị hiệ u dụ ng ( I, U, E)
-Góc pha đầ u (ψi,ψu,ψe)
u
u 2U sin( t )
e
e 2E sin( t )
i
i 2Isin( t )
Khi so sánh các đạ i lư ợ ng xoay chiề u hình sin cùng tầ n số :
=
u i
-So sánh về trị hiệ u dụ ng
-So sánh về góc pha :
m
U
U2
m
E
E2
Tư ơ ng tự :
Góc lệ ch pha giữ a điệ n áp và dòng điệ n :
4
1. Véc tơ :
Đặ c trư ng cho 1 véc tơ :
A
và 
A
Đặ c trư ng cho các đạ i lư ợ ng x/chiề u hình sin cùng tầ n số :
Trị hiệ u dụ ng ( I, U, E) và góc pha đầ u ( ψi,ψu,ψe)
Ký hiệ u
* Ư u điể m: Trự c quan
Đị nh luậ t
Kiế c-khố p
* Lư u ý:
k n
k
k 1
I 0
1 2
k n k n
k
k
k 1 k 1
U E
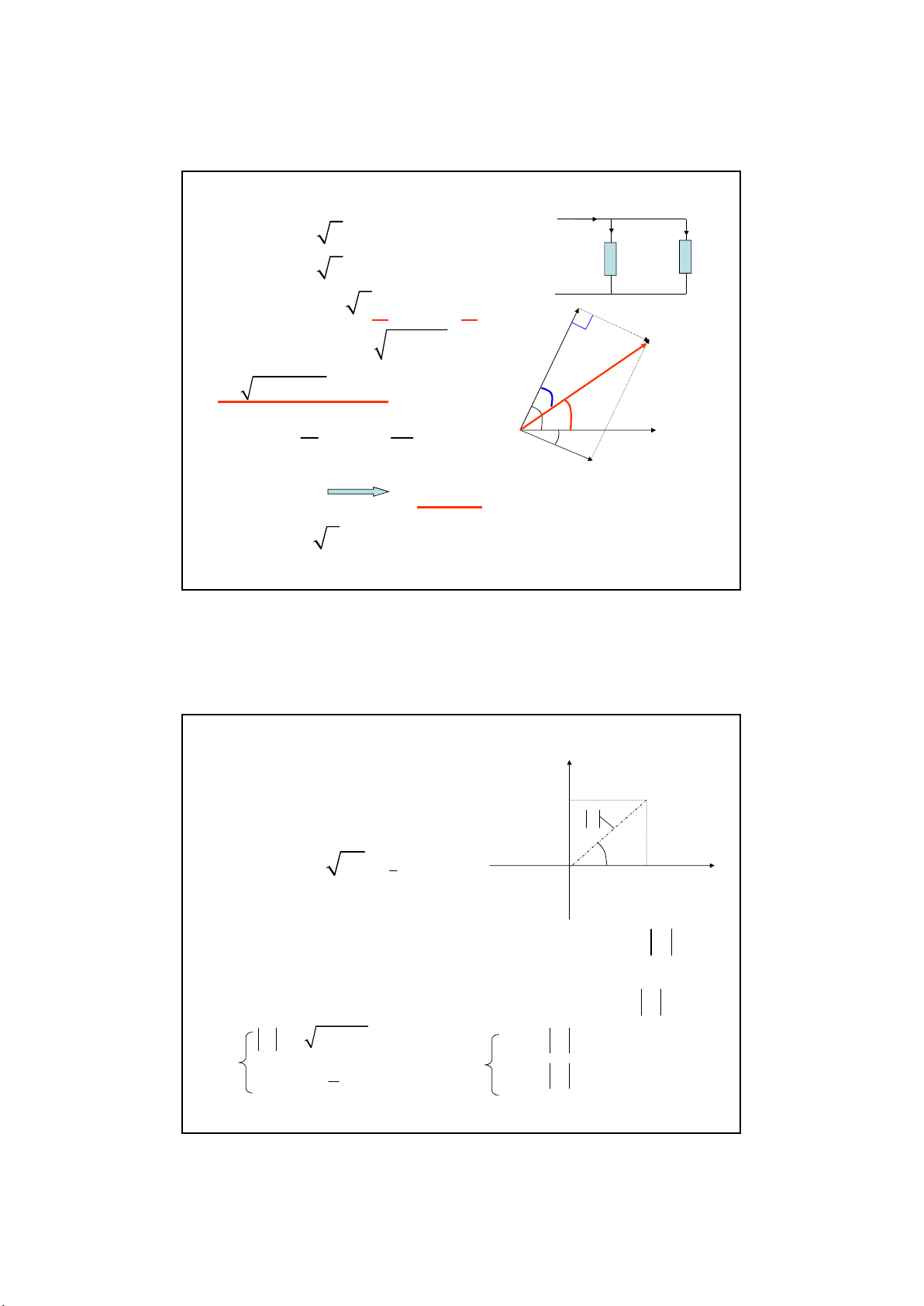
2.3 Biể u diễ n các đạ i lư ợ ng xoay chiề u hình sin
EUI
ox
ψu
ψi
ψe
E
I
U
A
x
0
18/01/2015
3
30o
Giả sử có mạ ch điệ n
Biế t :
0x
2
i
1
I
' arctg I
60o
Tìm : i = i1+ i2
i
i1i2
1
i 2.20sin( t 60 )
2
i 2.10sin( t 30 )
i
2.Isin( t )
2 2
1 2
I I I
2 2
I 20 10
= 22,36
ψi
ψi’
10
arctg 20
i' 26 34 '
i33 26'
i 2.22,36sin( t 33 26 ')
Kế t quả :
21 III
1
I
2
I
I
6
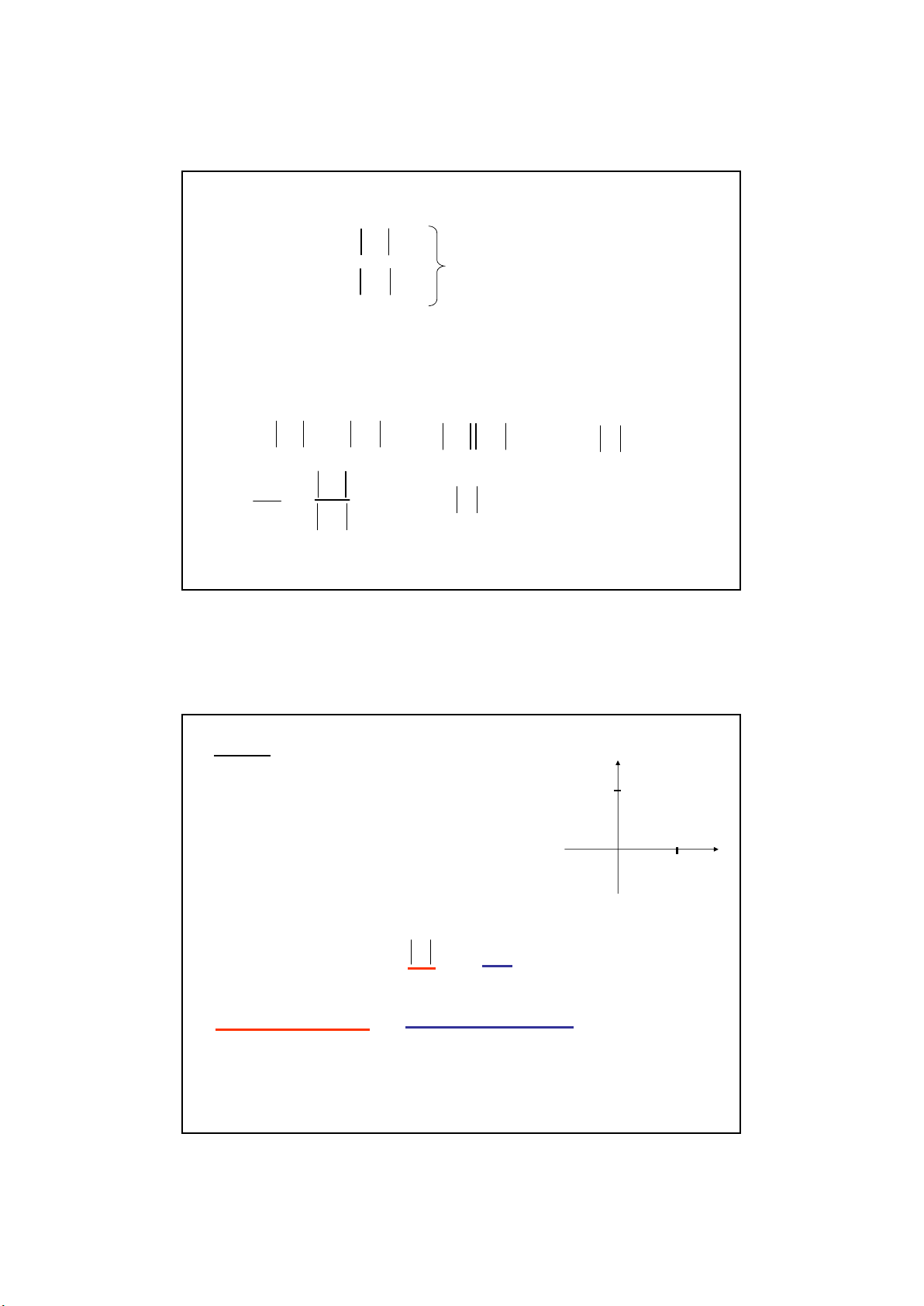
2. Số phứ c:
A = a + j b
A
+1
+j
0
a, b : số thự c
*Hai dạ ng biể u thị số phứ c:
Dạ ng đạ i số : A = a + j b Dạ ng lũy thừ a:
j
A A e
* Quan hệ giữ a 2dạ ng:
a. Nhắ c lạ i k/n về số phứ c
j: đơ n vị ả o
-Biế t dạ ng đạ i số : a + j b
A
2 2
a b
b
arctg a
1
1
j
- j
A
a
jb
j
A A e
Biế t dạ ng lũy thừ a:
a =
b =
A cos
A sin
18/01/2015
4
7
* Các phép tính + , - số phứ c
A1= a1+ j b1
= (a1±a2) + j (b1±b2) =
1
j
1
A e
A2= a2+ j b2
2
j
2
A e
* Các phép tính *, / số phứ c
(a1* a2-b1* b2) + j (a1b2+ a2b1) =
1
j
1
A e
2
j
2
* A e
1 2
j( )
1 2
A A e
j
A e
1
2
A
AA
j
A e
A = A1± A2= ?
a + j b
A = A1* A2= a + j b
1 2
1j( )
2
Ae
A
?
hoặ c
8
4. Chia 1 số cho j là quay số đó 1 góc (- 90o)
b. Biể u thị các đạ i lư ợ ng xoay chiề u hình sin bằ ng số phứ c :
Chú ý :
1. Khi làm các phép +,-
biể u thị dạ ng đạ i số
2. Khi làm phép *, /
biể u thị dạ ng lũy thừ a
3. Nhân 1 số vớ i j là quay số đó 1 góc 90o
Đặ c trư ng cho số phứ c :
A
và
Đặ c trư ng cho đạ i lư ợ ng xoay chiề u hình sin cùng tầ n số :
Trị hiệ u dụ ng ( I, U, E) và góc pha đầ u ( ψi,ψu,ψe)
Qui ư ớ c:
+1
+j
A = 3
B = A*j
= j3
i
j
I Ie
u
j
U Ue
e
j
E Ee
18/01/2015
5
9
C
C
1
U I
j C
i
j
LL
I I e
i
j
L
LI e
* Các phép tính đạ o hàm và tích phân số phứ c :
• Phép đạ o hàm : iLL
uL
Dạ ng tứ c thờ i
L
L
di
u L dt
Dạ ng phứ c:
L
L
jX I
ILXL
UL
XL
•Phép tích phân :
C
iC
uC
XC
IC
UC
Dạ ng tứ c thờ i:
C C
1
u i dt
C
Dạ ng số phứ c:
C
C
jX I
XC
I
j
L
L
d I
U L dt
k n
k
k 1
I 0
1 2
k n k n
k
k
k 1 k 1
U E
Đị nh luậ t Kiế c -khố p :
10
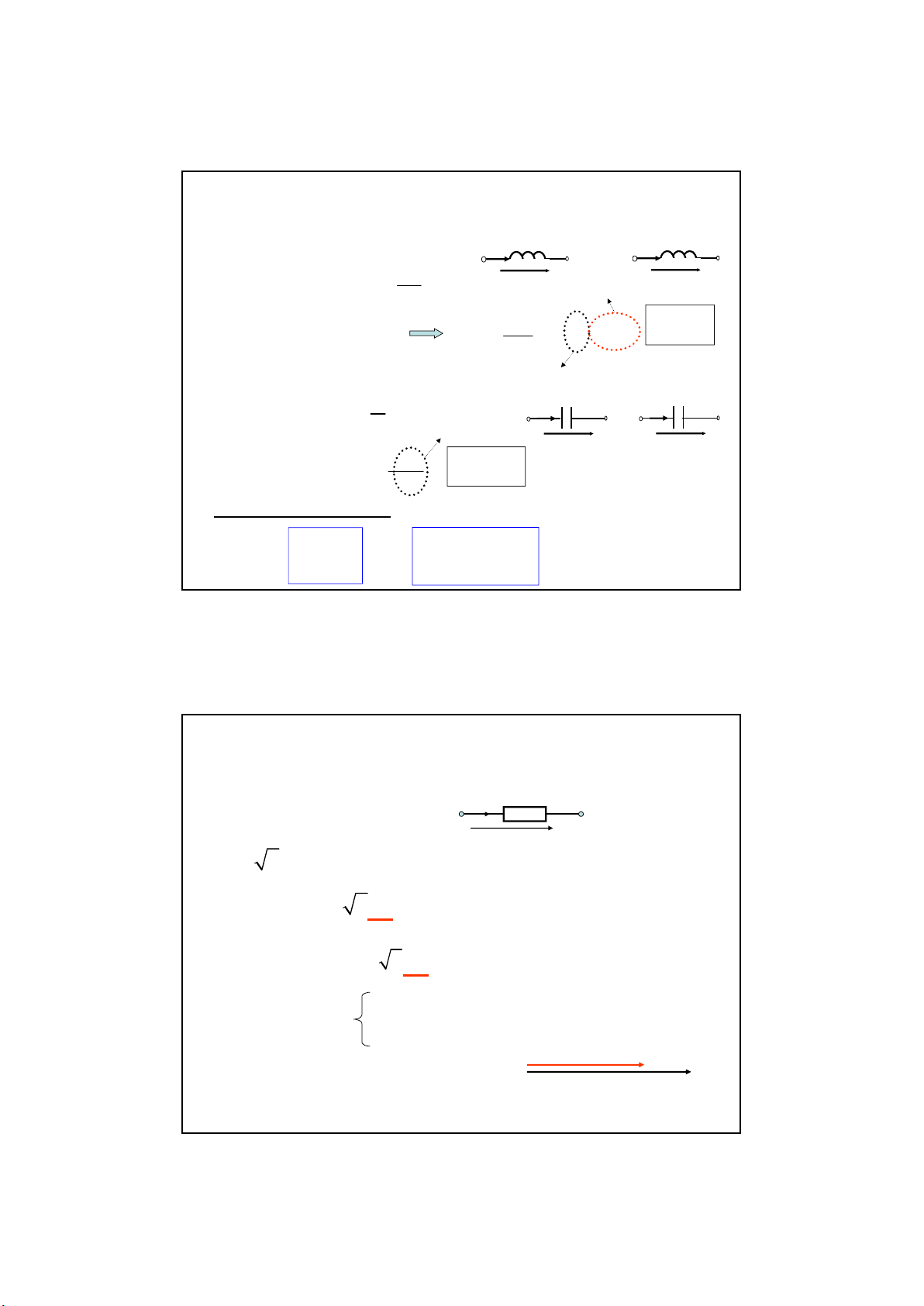
2.4 Phả n ứ ng củ a nhánh vớ i dòng điệ n xoay chiề u hình sin
1. Nhánh thuầ n trở R
iR
R R
i 2I sin t
R
2RI sin t
(2)
Biể u thứ c t/q :
R R u
u 2U sin( t )
(3)
=> uR= RiR
uR
( 1)
Từ (2) và (3) =>
R=ψu-ψi= 0
• Dạ ng véc tơ :
R
I
R
U
UR= RIRψu= 0