Assoc. Prof. Nguyễn Văn Nhận - Engineering Thermodynamics - 2007
Chương 2
ĐỊNH LUẬT NHIỆT ĐỘNG THỨ NHẤT
2.1. CÁC DẠNG NĂNG LƯỢNG THÔNG DỤNG
2.1.1. THẾ NĂNG ( Ep ) - còn gọi là ngoại thế năng - là năng lượng của lực
trọng trường.
E
p
= m. g. z = G. z
trong đó z là độ cao của vật so với bề mặt so sánh.
z
G
H. 2-1. Ngoại thế năng
2.1.2. ĐỘNG NĂNG (Ek) - còn gọi là ngoại động năng - là năng lượng
chuyển động vĩ mô của vật.
2
2
ω
⋅= mEK
2.1.3. NỘI NĂNG (U) - còn gọi là nội nhiệt năng - là năng lượng do chuyển
động của các phân tử bên trong vật và lực tương tác giữa chúng.
Nội năng gồm 2 thành phần : nội động năng (Ud) và nội thế năng (Up). Nội
động năng liên quan đến chuyển động của các phân tử nên nó phụ thuộc vào nhiệt độ
của vật. Nội thế năng liên quan đến lực tương tác giữa các phân tử nên nó phụ thuộc
vào khoảng cách giữa các phân tử. Như vậy, nội năng là một hàm của nhiệt độ và thể
tích riêng : U = U (T, v)
2.1.4. HÓA NĂNG (EC) - Năng lượng tích trữ trong các liên kết hóa học giữa
các nguyên tử trong phân tử.
2.1.5. NGUYÊN TỬ NĂNG (EA) - Năng lượng tích trữ trong các liên kết giữa
các hạt tạo nên hạt nhân của nguyên tử.
PDF created with pdfFactory trial version www.pdffactory.com
- 21 -
Assoc. Prof. Nguyễn Văn Nhận - Engineering Thermodynamics - 2007
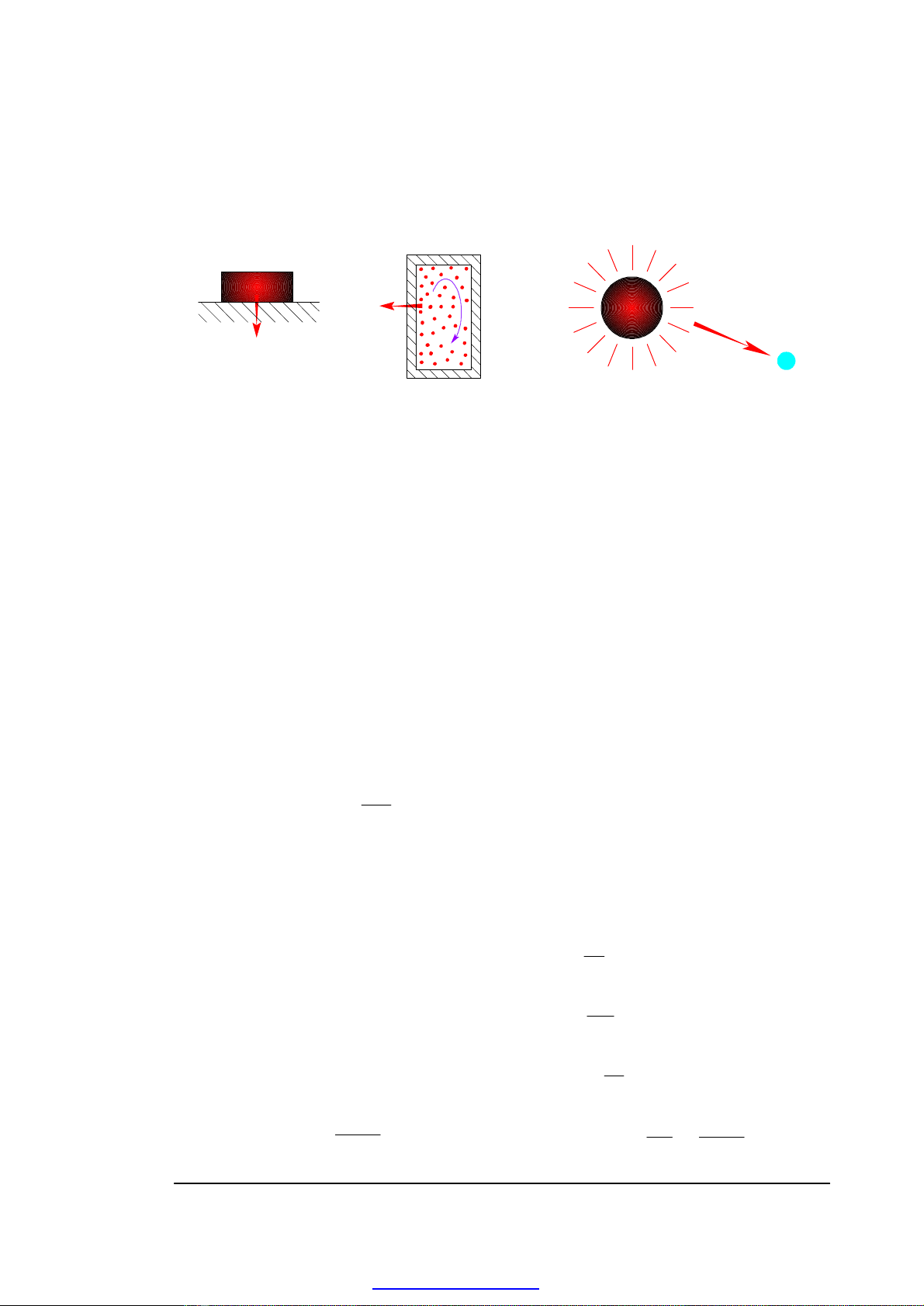
2.1.6. NHIỆT NĂNG (Q)
2.1.6.1. KHÁI NIỆM
Nhiệt năng là dạng năng lượng truyền từ vật này sang vật khác do sự chênh
lệch nhiệt độ.
Q
c)
Q
b)
Sun
Q
a)
Earth
H. 2-2. Các hình thức truyền nhiệt
Đơn vị đo nhiệt năng :
1) Calorie (Ca) - 1 Ca là nhiệt năng cần thiệt để làm nhiệt độ của 1 gram nước
tăng từ 14.5 0C đến 15.5 0C.
2) British thermal unit (Btu) - 1 Btu là nhiệt năng cần thiết để làm nhiệt độ của
1 pound nước tăng từ 59.5 0F lên 60.5 0F.
3) Joule (J) - 1 [J]
1 Ca = 4.187 J
1 Btu = 252 Ca = 1055 J
2.1.6.2. NHIỆT DUNG VÀ NHIỆT DUNG RIÊNG
Nhiệt dung của một vật là lượng nhiệt cần cung cấp cho vật hoặc từ vật tỏa ra
để nhiệt độ của nó thay đổi 1 0.
dt
dQ
C= [J/deg]
Nhiệt dung riêng (NDR) - còn gọi là Tỷ nhiệt - là lượng nhiệt cần cung cấp
hoặc tỏa ra từ 1 đơn vị số lượng vật chất để nhiệt độ của nó thay đổi 1 0.
• Phân loại NDR theo đơn vị đo lượng vật chất :
1) Nhiệt dung riêng khối lượng :
C
c
m
=
[J/kg .deg]
2) Nhiệt dung riêng thể tích :
tc
V
C
c=
' [J/m3t c .deg]
3) Nhiệt dung riêng mol :
()
N
C
c=µ [J/kmol .deg]
(
)
µ
c
vcc tc =⋅= ' ;
(
)
4,22
'c
v
c
c
tc
µ
==
PDF created with pdfFactory trial version www.pdffactory.com
- 22 -
Assoc. Prof. Nguyễn Văn Nhận - Engineering Thermodynamics - 2007
• Phân loại NDR theo quá trình nhiệt động :
1) NDR đẳng tích : cv , c'v , (µcv) .
2) NDR đẳng áp : cp , c'p , (µcp) .
• Công thức Maye :
c
p
- cv = R (2.1a)
(µc
p
) - (µcv) = Rµ = 8314 [J/kmol. deg] (2.1b)
• Chỉ số đoạn nhiệt :
v
p
c
c
k= (2.2)
Đối với khí lý tưởng : k = const
k = 1,6 - khí 1 nguyên tử,
k = 1,4 - khí 2 nguyên tử,
k = 1,3 - khí nhiều nguyên tử.
• Quan hệ giữa c, k và R :
Từ (2.1) và (2.2) ta có :
R
k
cv⋅
−
=
1
1 ; R
k
k
cp⋅
−
=
1
(2.3)
• Nhiệt dung riêng của khí thực :
NDR của khí thực phụ thuộc vào bản chất của chất khí, nhiệt độ, áp suất và quá
trình nhiệt động :
c = f(T, p, Quá trình).
Trong phạm vi áp suất thông dụng, áp suất có ảnh hưởng rất ít đến NDR. Bởi
vậy có thể biểu diễn NDR dưới dạng một hàm của nhiệt độ như sau :
c = a0 + a1. t + a2. t 2 + ..... + an. tn (2.4)
• Nhiệt dung riêng của khí lý tưởng :
NDR của khí lý tưởng không phụ thuộc vào nhiệt độ và áp suất.
Bảng 2-1. Nhiệt dung riêng của khí lý tưởng
Loại khí (µc
v
) [kJ/kmol. deg] (µc
p
) [kJ/kmol. deg]
Khí 1 nguyên tử 12,6 20,9
Khí 2 nguyên tử 20,9 29,3
Khí nhiều nguyên tử 29,3 37,4
• Nhiệt dung riêng của hỗn hợp khí
∑
=
⋅= n
i
ii cgc
1; ∑
=
⋅= n
i
ii crc
1
'' ;
()()
∑
=
⋅=
n
i
ii crc
1
µµ (2.5)
PDF created with pdfFactory trial version www.pdffactory.com
- 23 -
Assoc. Prof. Nguyễn Văn Nhận - Engineering Thermodynamics - 2007
2.1.6.3. TÍNH NHIỆT DUNG RIÊNG TRUNG BÌNH
Khi biết NDR trung bình trong khoảng nhiệt độ 0 ÷ t, có thể tính trung bình
trong khoảng nhiệt độ t1 ÷ t2 như sau :
• NDR trung bình trong khoảng nhiệt độ 0 ÷ t :
001
|
t
caat
=+⋅
• Theo định nghĩa NDR :
dq
c
dt
=
• Nhiệt trao đổi trong quá trình 1 - 2 :
()
2
22
11
1
21
||
t
tt
tt
t
qcdtctt
=⋅=⋅−
∫ (2.6a)
• Mặt khác có thể viết :
(
)
(
)
00 1
0
2
000
12122
1−⋅−−⋅=−= tctcqqq ttttt
t
1
0
2
0
12 tctc tt ⋅−⋅= (2.6b)
• Từ (2.6a) và (2.6b) ta có :
()
21
2
1
21
00
0121
21
tt
t
t
ctct
caatt
tt
⋅−⋅
==+⋅+
−
2.1.6.4. TÍNH NHIỆT THAM GIA QUÁ TRÌNH
• Căn cứ vào nhiệt dung riêng :
()
2
22
11
1
21
||
t
tt
tt
t
qcdtctt
=⋅=⋅−
∫
• Căn cứ vào định luật nhiệt động 1 (xem chương 2) :
q = ∆u + w
• Căn cứ vào entropy :
∫
⋅=
2
1
T
T
dsTq
PDF created with pdfFactory trial version www.pdffactory.com
- 24 -
Assoc. Prof. Nguyễn Văn Nhận - Engineering Thermodynamics - 2007
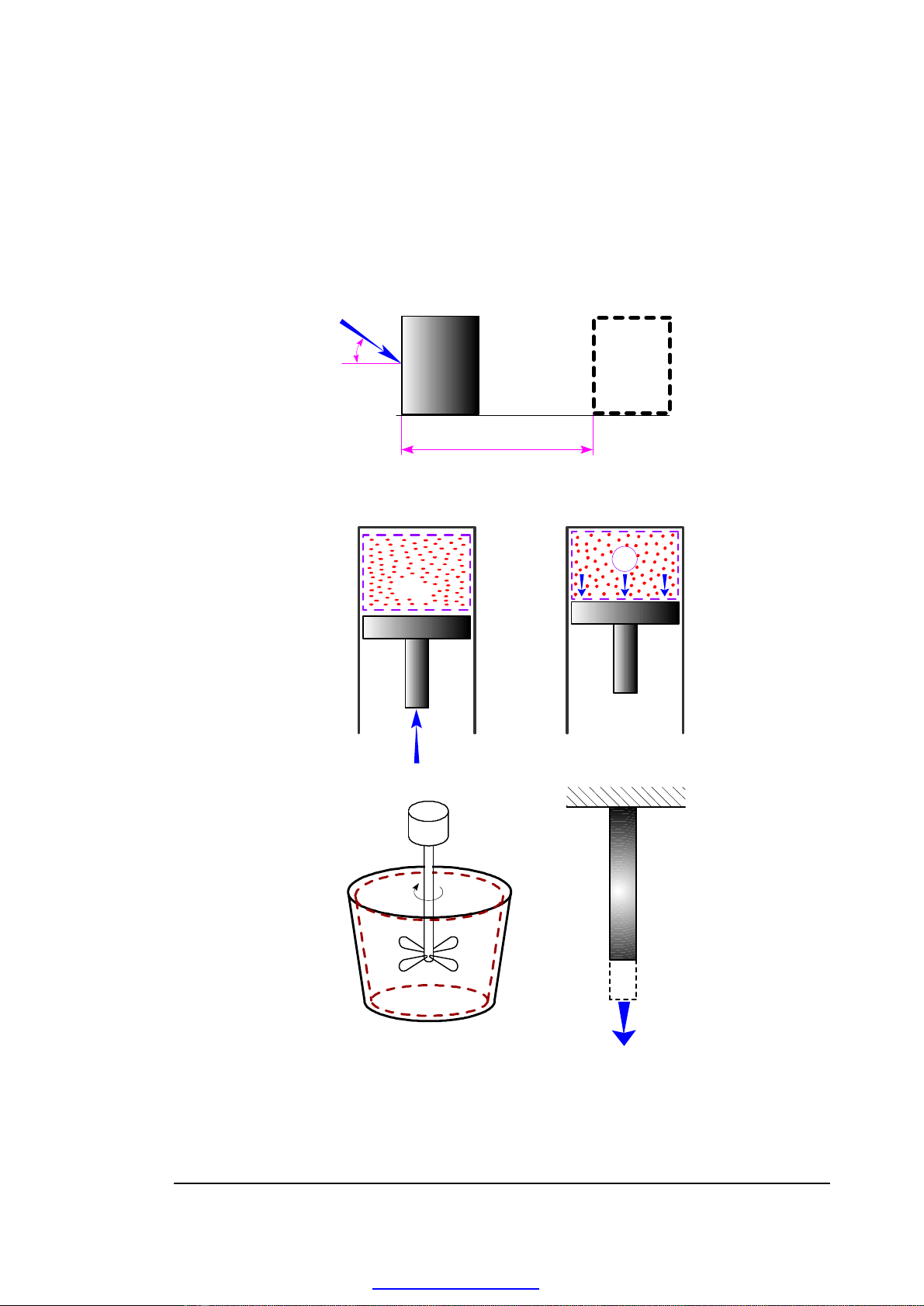
2.1.7. CÔNG
2.1.7.1. KHÁI NIỆM
Công - còn gọi là cơ năng - là dạng năng lượng hình thành trong quá trình biến
đổi năng lượng trong đó có sự dịch chuyển của lực tác dụng. Về trí số, công bằng tích
của thành phần lực cùng phương chuyển động và quãng đường dịch chuyển.
W = (F. cosθ). S
S
θ
F
H. 2-5.
F
F
p
a)b)
c)d)
H. 2-6. Các hình thức thực hiện công
PDF created with pdfFactory trial version www.pdffactory.com