1
Các phương pháp thiết kế thuật giải
Trịnh Huy Hoàng
Khoa Công nghệ thông tin
Đại học Sư phạm TPHCM
2
Nội dung
Thiết kế thuật toán
Phân loại các phương pháp thiết kế thuật toán
Các thuật toán chính xác
Các thuật toán gần đúng
Các bước để thiết kế một thuật giải cho một vấn
đề cho trước
3
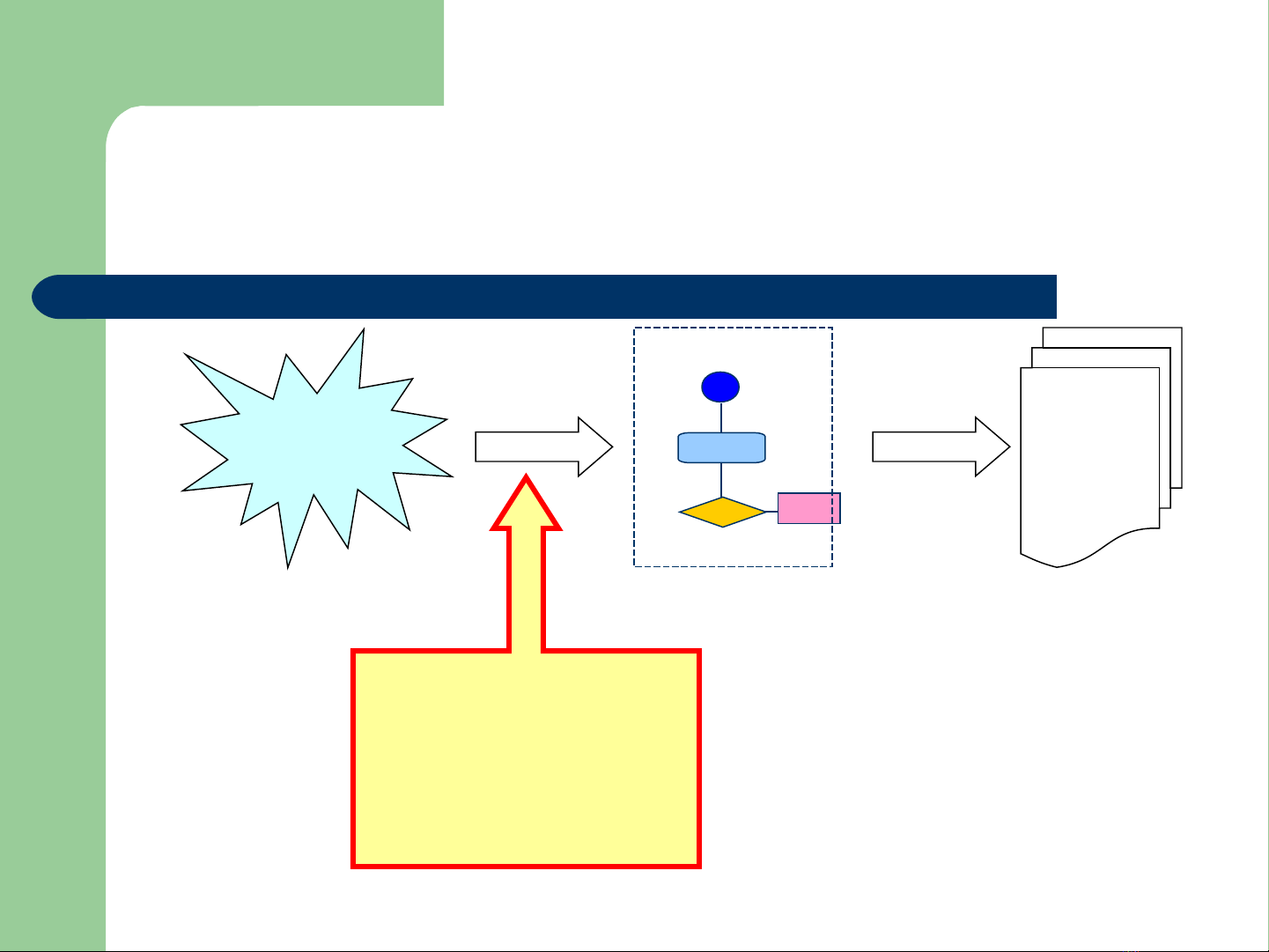
Mô hình từ bài toán đến chương trình
Bài toán
th c tự ế
Thi t kế ế L p trìnhậ
Gi i thu tả ậ
#includ
e …
Ch ng ươ
trình
K thu t thi t k gi i ỹ ậ ế ế ả
thu t:ậ
Chia đ tr , quy ho ch ể ị ạ
đng, …ộ
Các bước để giải 1 bài toán trên
máy tính
Bước 1: Xác định vấn đề - bài toán
Bước 2: Lựa chọn phương pháp giải
Bước 3: Xây dựng thuật toán hoặc thuật giải
Bước 4: Cài đặt chương trình
Bước 5: Hiệu chỉnh chương trình
Bước 6: Thực hiện chương trình
4
5
Thiết kế một thuật toán
Cho một vấn đề cần giải quyết
Xác định các bước và trình tự các bước để
giải quyết vấn đề đó
Phân tích thuật toán tốt đến mức nào