

Khoa
KH & KTMT
©2012, CE Department
Khoa
KH & KTMT
Bộmôn KỹThuật Máy Tính


Tài liu tham kho
• “Digital Systems, Principles and Applications”,
8th/5th Edition, R.J. Tocci, Prentice Hall
• “Digital Logic Design Principles”, N.
Balabanian & B. Carlson
–
John Wiley &
Logic Design 1 ©2012, CE Department
Balabanian & B. Carlson
–
John Wiley &
Sons Inc., 2004
2


Các
phép toán và
Các
phép toán và
mạch số học
©2012, CE Department


Phép cng nh phân
• Phép cng (Addition) là phép toán quan trng nht
trong các hthng s
– Phép tr(Subtraction), phép nhân (multiplication) và phép
chia (division)đưc hin thc bng cách sdng phép
cng
– Lut cơbn: 0+0=0
1+0=1
1+1=10 =0+carry of 1 into next position
1+1+1=11 =1+carry of 1 into next position
– Ví d
Logic Design 1 ©2012, CE Department 4


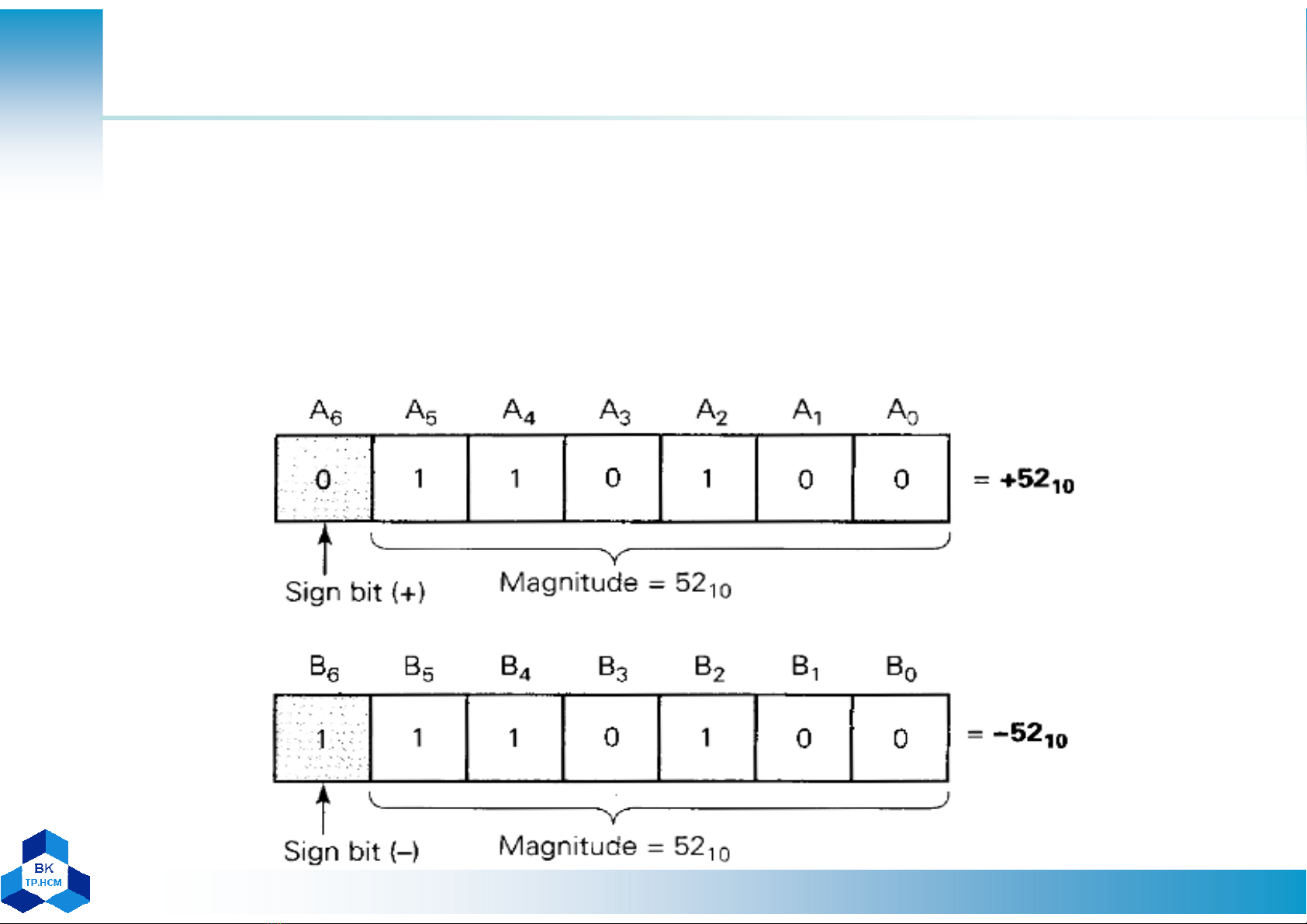
Biu din s có du (1)
• Bit du (sign bit)
0: dương (positive) 1: âm (negative)
• Lưng s(magnitude)
• Hthng sign-magnitude
Logic Design 1 ©2012, CE Department 5