
ng i
Tính chtng i ngn nht
ng i ngn nht tmtnh
Thut toán Dijkstra
ng i ngn nht gia minh
Thut toán Floyd–Warshall

a
Trong thvô hng = ,
ng i
là dãy các nh , , … ,
2 nh liên tip, c ni bi 1 cnh trong .
c gi là ng i tn
Chu trình
là ng i, , … , vi > 1
trong ónh u tiên phân bit và =
Vi thcó hng, trong mtng i hay
chu trình, 2 nh liên tip(, )phi là mt
cung thuc
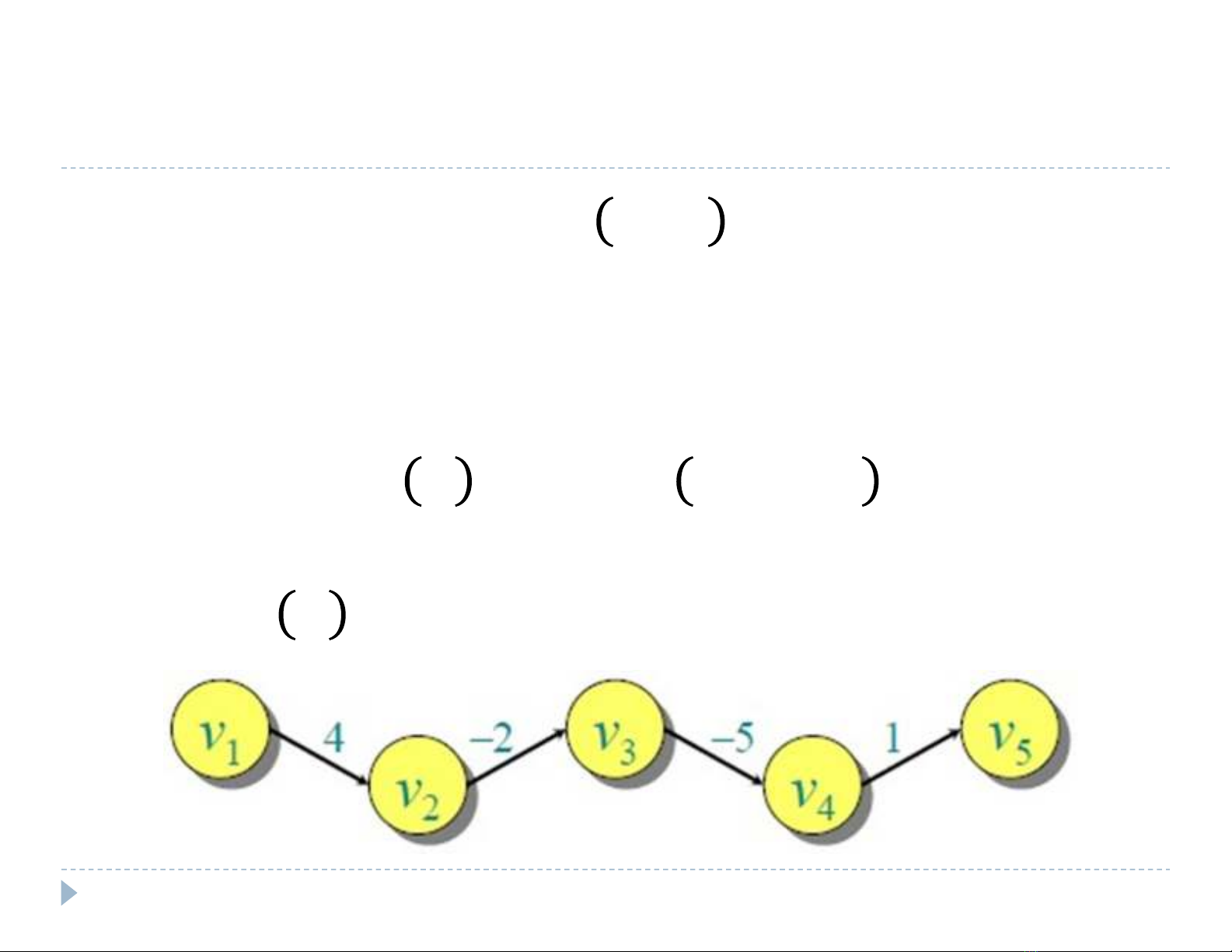
thcó hng = vi hàm trng s
cung . Trng scang i
cnh ngha:
Ví d:

a
ng i ngn nht (NN) tn là
ng i có trng snhnht tn .
Trng s ng i ngn nht tn
cnh ngha:
, = min : đườngđitừđến
Chú ý: , = ∞không tn ting i
tn.

![Bài giảng Phân tích thiết kế và đánh giá thuật toán Trường ĐH Hàng Hải [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250909/oursky06/135x160/58071768925368.jpg)
























